Step 1: Gathering Prime Number Candidates

We'll start by creating an array of integers up to n+1. Since prime numbers must be natural numbers greater than 1, we can discard 0 and 1.

Here's a visual representation of what we're doing:

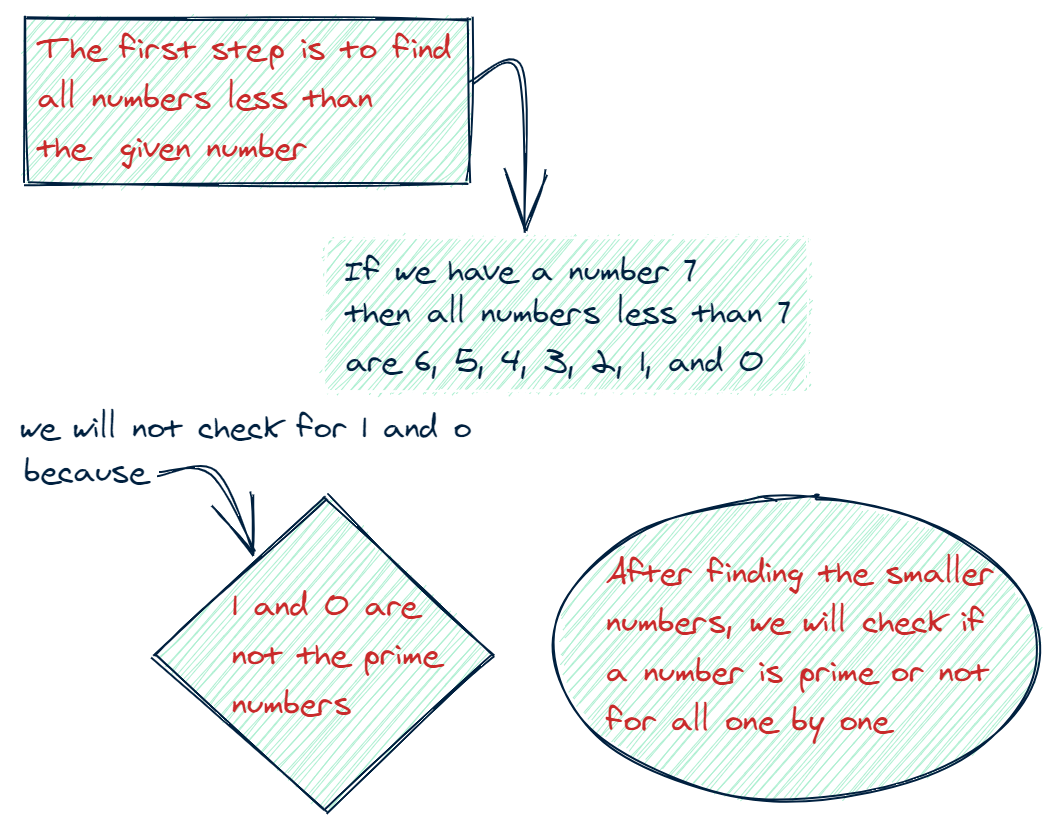
Here's how we initialize our candidates in both JavaScript and Python:

1const n = 4;
2const numsLessThanN = Array.from(
3  { length: n + 1 }, function(val, idx) {
4    return idx;
5  }
6).slice(2);

This provides us with all potential prime number candidates smaller than n.

The easiest way is through this piece of logic: while a number can be prime and greater than 1, try dividing it by prime numbers greater than its square root. For example, say we have 6-- it's square root is ~2.449. So we try to divide it by 3, the next greater prime number, but we realize it is divisible and thus not prime. We'll expand on the logic for this shortly!

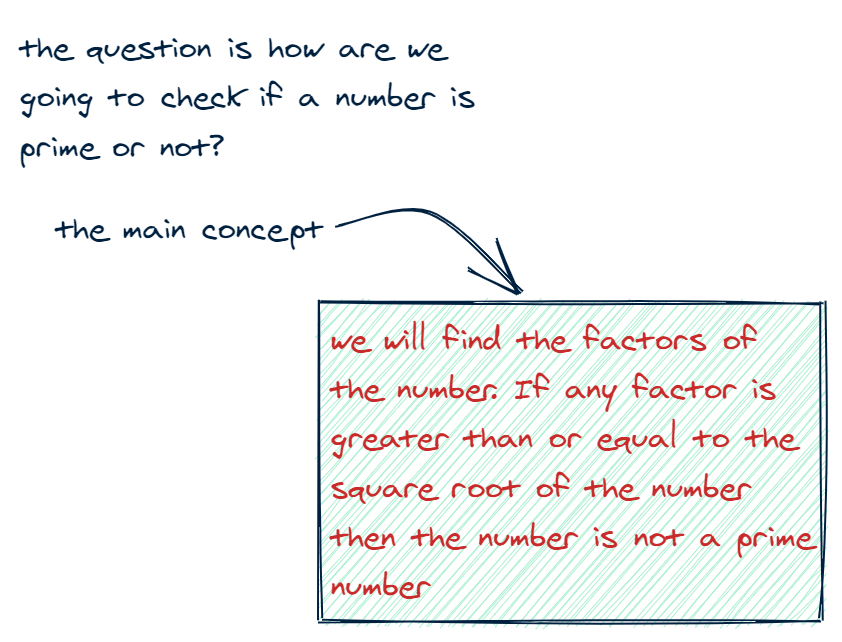
1const primes = numsLessThanN.filter((num) => {
2  let primeCandidate = num - 1;
3
4  while (primeCandidate > 1 && primeCandidate >= Math.sqrt(num)) {
5    if (num % primeCandidate === 0) return false;
6    primeCandidate--;
7  }
8
9  return true;
10});

Complexity of Final Solution

Let n be the input number. We fill an array of size n to keep track of potential prime candidates for O(n) space complexity, and our while loop that updates our array performs roughly log n work over n iterations for O(n log n) time complexity.

Here's why it works: if a number is divisible by a prime number, then it itself is not a prime number.

On the flip side, the number must be divisible beyond its square root. The intuition here saves us several calculations, and can be understood with the following:

• If n isn't prime, it should be able to be factored into x and y. In our previous example, 6 could be factored into 2 and 3.
• If both x and y were greater than the square root of n, it would confirm that x * y would produce a number larger than n. In this case, only 3 is larger than the square root.
• This means at least one of the factors needs to be less than or equal to the square root of n. If we don't find any factors that fit, that are greater than or equal to the square root, we know that n must be a prime number. However, we found 3-- so 6 can't be prime.

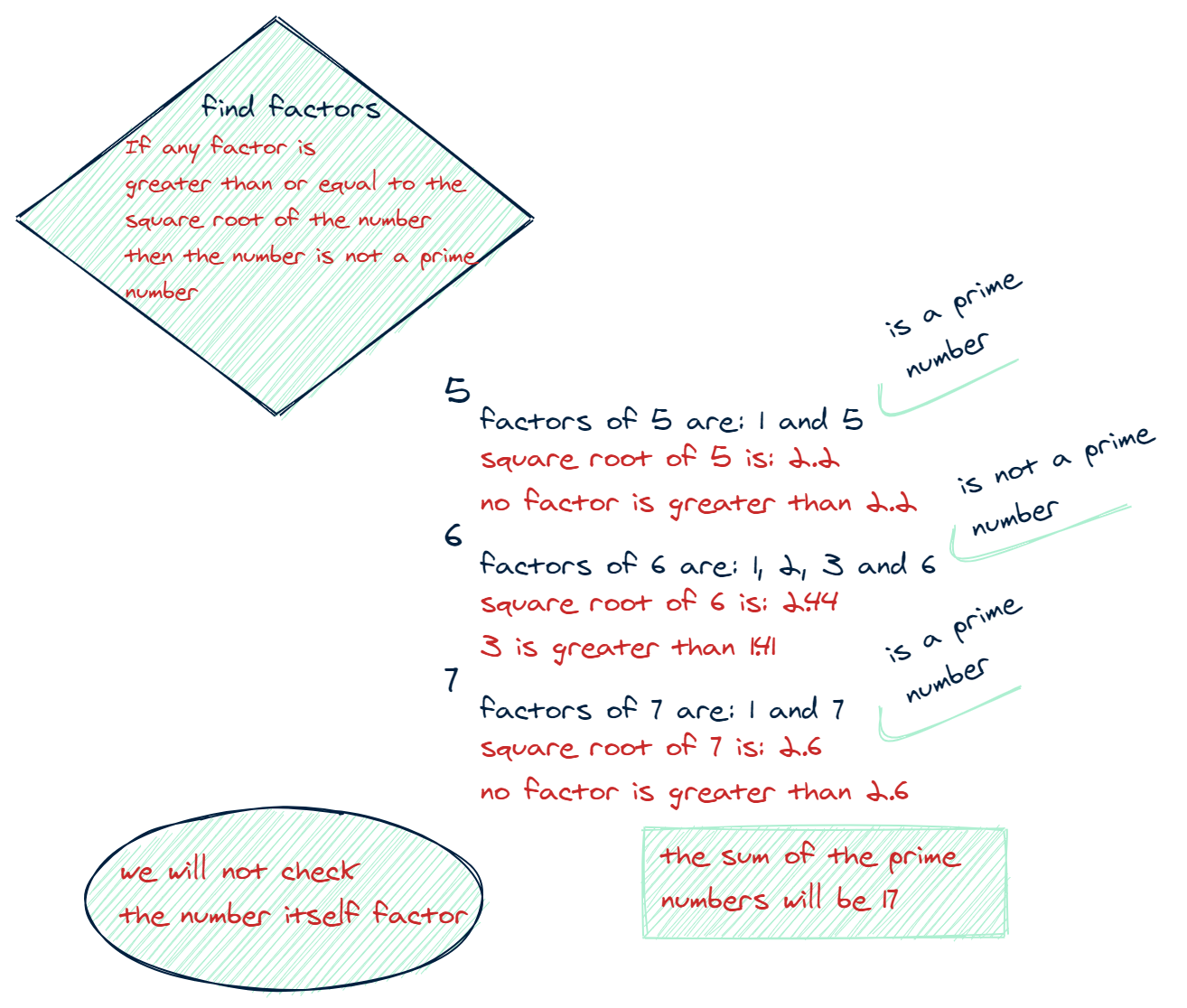
Let's take the number 7, and run the numbers smaller than it through this filter:

• Starting at 7, passes the conditions, returns true.
• 6, we find that 6 is divisible by 3, so remove it.
• 5 passes the conditions, returns true.
• 4 is divisible by 2, get rid of it as well.
• 3 passes the conditions, returns true.
• 2 passes the conditions, returns true.
• We throw out 0 and 1 since they're not prime.

So we get 17 once they're summed up.

One Pager Cheat Sheet

• Write a method sumOfAllPrimes that takes a number n and returns the sum of all prime numbers smaller than or equal to n.
• We can use an array of length n+1 initialized with natural numbers starting from 2, and removing 0 and 1, to programmatically determine what numbers are prime.
• We can figure out the prime number candidates that are smaller than n with an O(n^2) operation by looping through every number from 2 to the current one and seeing if it is divisible.
• We can check for prime numbers efficiently by looping over the numbers below n and performing a log n time operation to check divisibility by prime numbers larger than the square root of n.
• We can use a filter that requires a number to be divisible beyond its square root in order to determine if it is a prime number, which allows us to efficiently find and sum all prime numbers.

This is our final solution.

To visualize the solution and step through the below code, click Visualize the Solution on the right-side menu or the VISUALIZE button in Interactive Mode.

xxxxxxxxxx

}

var assert = require('assert');

​

function sumOfPrimes(n) {

  const numsLessThanN = Array.from({ length: n + 1 }, function (val, idx) {

    return idx;

  }).slice(2);

​

  const primes = numsLessThanN.filter((num) => {

    let primeCandidate = num - 1;

​

    while (primeCandidate > 1 && primeCandidate >= Math.sqrt(num)) {

      if (num % primeCandidate === 0) return false;

      primeCandidate--;

    }

​

    return true;

  });

​

  return primes.reduce((prime1, prime2) => prime1 + prime2);

}

​

try {

  assert.deepEqual(2, sumOfPrimes(2), 'sumOfPrimes(2) should equal 2');

​

  console.log('PASSED: ' + '`sumOfPrimes(2)` should equal `2`');

} catch (err) {

  console.log(err);

}

​

try {

  assert.deepEqual(129, sumOfPrimes(30), 'sumOfPrimes(30) should equal 129');

​

You're doing a wonderful job. Keep going!

If you had any problems with this tutorial, check out the main forum thread here.