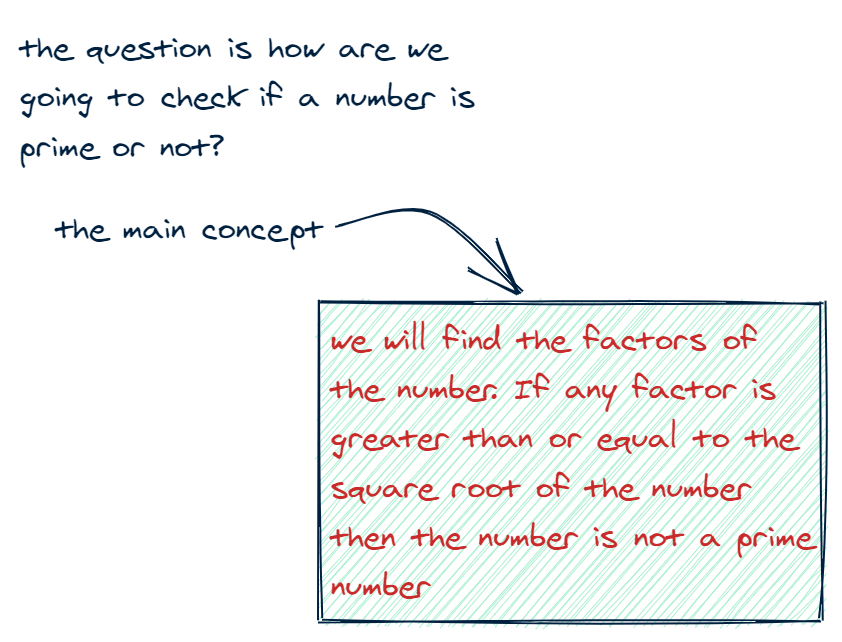
The easiest way is through this piece of logic: while a number can be prime and greater than 1, try dividing it by prime numbers greater than its square root. For example, say we have 6-- it's square root is ~2.449. So we try to divide it by 3, the next greater prime number, but we realize it is divisible and thus not prime. We'll expand on the logic for this shortly!

1const primes = numsLessThanN.filter((num) => {
2  let primeCandidate = num - 1;
3
4  while (primeCandidate > 1 && primeCandidate >= Math.sqrt(num)) {
5    if (num % primeCandidate === 0) return false;
6    primeCandidate--;
7  }
8
9  return true;
10});

Complexity of Final Solution

Let n be the input number. We fill an array of size n to keep track of potential prime candidates for O(n) space complexity, and our while loop that updates our array performs roughly log n work over n iterations for O(n log n) time complexity.