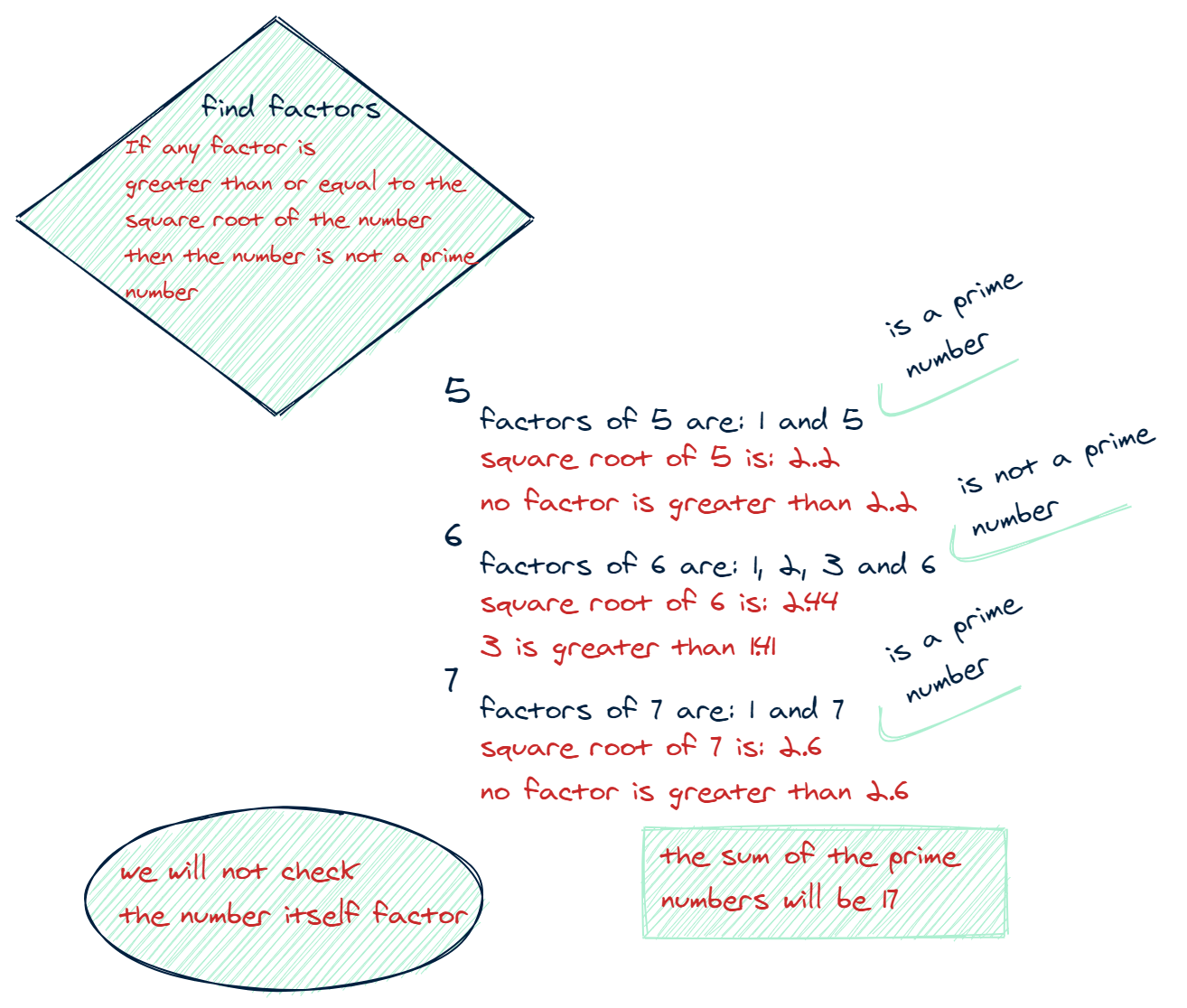
Here's why it works: if a number is divisible by a prime number, then it itself is not a prime number.

On the flip side, the number must be divisible beyond its square root. The intuition here saves us several calculations, and can be understood with the following:

• If n isn't prime, it should be able to be factored into x and y. In our previous example, 6 could be factored into 2 and 3.
• If both x and y were greater than the square root of n, it would confirm that x * y would produce a number larger than n. In this case, only 3 is larger than the square root.
• This means at least one of the factors needs to be less than or equal to the square root of n. If we don't find any factors that fit, that are greater than or equal to the square root, we know that n must be a prime number. However, we found 3-- so 6 can't be prime.

Let's take the number 7, and run the numbers smaller than it through this filter:

• Starting at 7, passes the conditions, returns true.
• 6, we find that 6 is divisible by 3, so remove it.
• 5 passes the conditions, returns true.
• 4 is divisible by 2, get rid of it as well.
• 3 passes the conditions, returns true.
• 2 passes the conditions, returns true.
• We throw out 0 and 1 since they're not prime.

So we get 17 once they're summed up.