AlgoDaily - Kadane's Algorithm Explained

Home > Data Structures and Algorithms 🚀 > Dynamic Programming Interview Questions > Kadane's Algorithm Explained

Kadane's Algorithm is a powerful technique used to solve the Maximum Subarray Problem. This lesson is designed to guide you step-by-step through understanding the problem, exploring different solutions, and finally, mastering Kadane's Algorithm itself. Here's what we'll cover:

1) Kadane’s Algorithm at a Glance (Why this matters)

What is it? A lightning-fast way to find the most profitable “streak” in an array—i.e., the contiguous subarray with the highest sum.
Where it shines: Stock gains over days, longest “winning run” in signal processing, anytime you care about the best contiguous chunk.
Why people love it: It runs in O(n) time with O(1) extra space. Translation: fast and tiny.

2) Meet the Maximum Subarray Problem (with a picture in your head)

The problem: Given an array (which can include negatives), find the contiguous slice with the biggest sum.
Mental model: Imagine walking a trail with ups (+) and downs (–). Your goal is to pick one continuous stretch that climbs the most overall.
Quick example: [-2, 1, -3, 4, -1, 2, 1, -5, 4] → best subarray is [4, -1, 2, 1] with sum 6.

3) Brute Force (the “try everything” approach)

Idea: Check every possible start and end index, compute each sum, keep the best.
Pros: Dead simple, great for understanding the problem.
Cons: Slow when arrays get big.
Time complexity: O(n²) sums (or O(n³) if you recompute sums every time).

4) Brute Force in Code (get it working first)

We’ll write the straightforward version so you can see the mechanics: nested loops, track a running best, done.
This gives you a baseline to compare against Kadane’s speedup later.

5) Kadane’s Algorithm (the elegant upgrade)

Core idea: As you scan left → right, keep a running sum.
- If the running sum ever goes negative, drop it and start fresh at the next element.
- Track the best sum you’ve seen along the way.
Why it works: A negative running sum can only hurt future totals—so reset early and often.
Steps you’ll follow:
1. Initialize best and current with the first element.
2. For each next number x: current = max(x, current + x) best = max(best, current)
3. Return best.
Time complexity: O(n). One pass. No extra storage. Chef’s kiss.

6) Kadane in Code (concise and fast)

We’ll implement Kadane in a few popular languages so you can copy, paste, and profit (academically).
You’ll see it’s 3–5 lines for the core logic—clean, tight, and interview-ready.

What you’ll walk away with

By the end, you’ll:

Understand the Maximum Subarray Problem clearly.
Have a working brute-force solution (for learning and testing).
Master Kadane’s Algorithm and know why it’s optimal.
Be ready to spot and solve “best contiguous streak” problems on sight.

Kadene's Algorithm Overview

Let's dive into the intriguing world of Kadane's Algorithm and explore how it provides an optimal solution to the Maximum Subarray Problem. We'll go through the key aspects, the problem it solves, and why it's an important method in the field of computer science.

Joseph Born Kadane and His Contribution

Joseph Born Kadane, a renowned statistician, is known for his early support of Bayesian statistics. He introduced Kadane's Algorithm at a seminar at Carnegie Mellon University. But what's so special about this algorithm? Let's delve into it.

The Problem: Maximum Subarray

The algorithm addresses a well-known problem in computer science called the Maximum Subarray Problem. Imagine having an array of integers, and you need to find a contiguous subarray that has the maximum sum. Sounds challenging, right? Here's where Kadane's Algorithm shines!

Dynamic Programming: Breaking It Down

Kadane's Algorithm falls under the category of Dynamic Programming. It's like solving a complex puzzle by breaking it down into smaller pieces:

Solve a Subproblem: Work on a small part of the problem.
Save the Solution: Keep the solution of that part in memory.
Reuse the Solution: If the same subproblem occurs, use the saved solution instead of solving it again.

This approach ensures efficiency and speed, as it avoids redundant computations.

How Kadane's Algorithm Works

Initialize Two Variables: One for the current sum (currentSum) and another for the maximum sum found so far (maxSum).
Iterate Through the Array: For each element, calculate the currentSum by adding the element to the previous currentSum. If the currentSum becomes negative, reset it to zero.
Update maxSum: If the currentSum is greater than maxSum, update maxSum.
Result: The value in maxSum is the maximum sum of a contiguous subarray.

Maximum Subarray Problem

Given an input array of size n, the Maximum Subarray Problem is to find the largest sum of a contiguous subarray within that input array. Let's understand this through an example:

In the above example, we can see that the largest sum of a contiguous subarray in the input array of size 7 is 11. Now how can we find this programmatically?

Let's dive deep into finding a solution to this problem!

Assumptions

There are no empty subarrays within the input array.
globalMaxSum denotes the largest sum of a contiguous subarray in an input array.
localMaxSum at index i denotes the largest sum of the subarrays starting with the element at input[i].
n is the size of the input array.

Brute Force Approach

The simplest solution to the problem is using the Brute Force approach:

Find all the possible contiguous subarrays.
Calculate their sum.
Find the maximum of all the sums.

Now going back to our input array to understand the Brute Force solution to the problem:

In the above example, we can see that we'll have to calculate the sum of all the possible contiguous subarrays starting at index 0 to n-1. The above illustration is for index 0. The same step will be repeated for all the indices. Let's understand this solution to find the globalMaxSum:

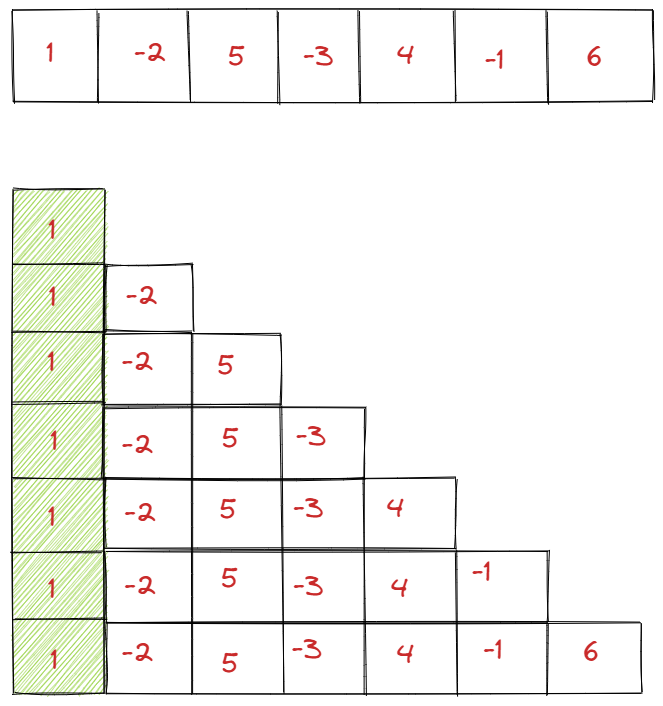
This approach will require two loops.
An outer loop with index i that will iterate from 0 to n-1.
An inner loop with index j that will iterate from j set to i to n-1.
The inner loop will calculate subArraySum:

SNIPPET

1subArraySum = subArraySum + input[j]

Meanwhile, subArraySum will be compared with globalMaxSum.
If globalMaxSum will be less than subArraySum, then globalMaxSum will be set to subArraySum.
In the end, we'll be able to find out the largest sum of a contiguous subarray.
Note that the time complexity for this algorithm is O(n²)

Now heading to implementation in code to get a clearer understanding:

xxxxxxxxxx
 
function solveMaxSubArrayProblem(input)
{
    var n = input.length
    var globalMaxSum = Number.MIN_VALUE
    var subArraySum
      
        for (var i = 0; i < n ; i++) {
            subArraySum= 0;
            for (var j = i; j < n; j++) {
            subArraySum+= input[j]
            if (subArraySum> globalMaxSum) {
                globalMaxSum = subArraySum
            }
            }
        }
    return globalMaxSum
}
  
var input = [ 1, -2, 5, -3, 4, -1, 6 ]
var result = solveMaxSubArrayProblem(input)
document.write(result)

Try this exercise. Click the correct answer from the options.

What is the time complexity to find the largest sum of a contiguous subarray using the Brute Force Approach?

Click the option that best answers the question.

O(n)
O(1)
O(log n)
None of the above

Kadane's Algorithm - Unpacking an Optimal Solution

To thoroughly understand Kadane's Algorithm, we'll examine an example array: [1, -2, 5, -3, 4, -1, 6]. Here's an illustrative representation:

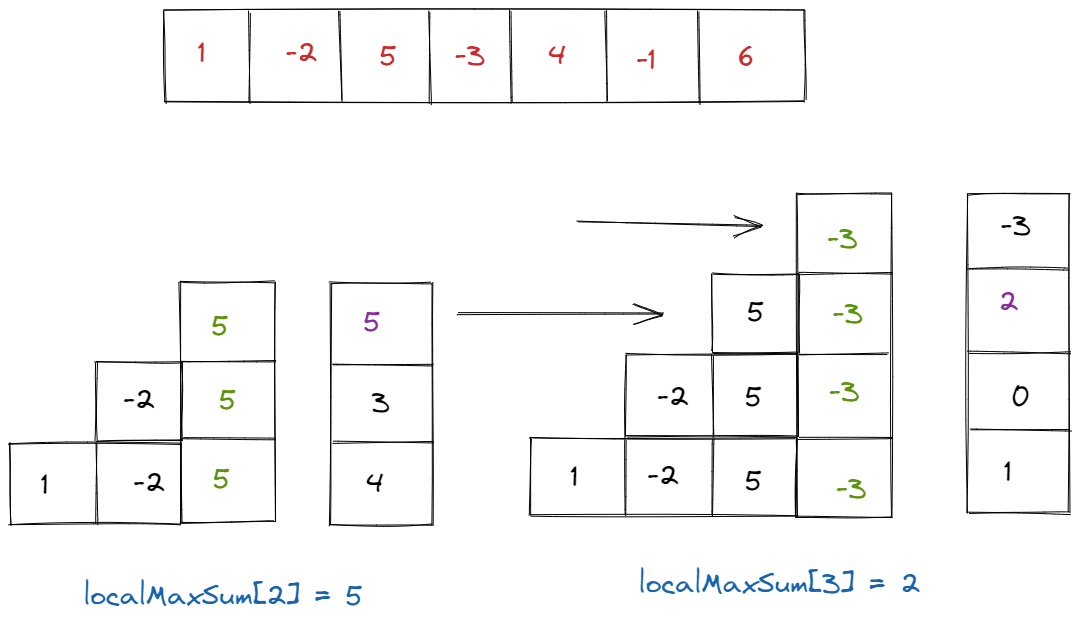
Introducing the Concept of "localMaxSum"

The key concept in Kadane's Algorithm is "localMaxSum," which represents the maximum sum of a contiguous subarray ending at a specific index. By keeping track of this "local" maximum, we can efficiently find the "global" maximum sum across the entire array.

Exploring localMaxSum[3]

Why are we looking at localMaxSum[3]? It's a pivotal point in understanding the algorithm. By examining this specific index, we can gain insights into how the algorithm builds solutions progressively. Let's break it down:

Possible Contiguous Subarrays

A "contiguous subarray" means a continuous sequence of elements within the array. For localMaxSum[3], the possible contiguous subarrays are:

[-3] // index 3 only
[5,-3] // index 2 & 3
[-2,5,-3] // index 1, 2 & 3
[1,-2,5,-3] // index 0, 1, 2 & 3

These combinations represent different ways to sum the elements ending at index 3. Among these, the combination [5,-3] sums up to 2, and therefore, the localMaxSum[3] is found to be 2.

An Insightful Observation

Now, let's compare localMaxSum[3] with localMaxSum[2]. What distinguishes them? It's only the element -3 at index 3. To find localMaxSum[3], we need the previous localMaxSum[2] and the element at index 3.

The Insight's Significance

This observation forms the heart of Kadane's Algorithm. It tells us that the localMaxSum at index i depends on only two factors: 1. The current element at index i. 2. The localMaxSum at the previous index i-1.

This relationship simplifies the problem significantly and leads to an efficient solution.

Implementing Kadane's Algorithm

Now, let's translate our understanding into practical steps and code:

Loop Through the Array: Iterate from index 0 to n-1.

Calculate localMaxSum: Use the formula:

SNIPPET

1localMaxSum[i] = max(input[i], input[i] + localMaxSum[i-1])

Compare with globalMaxSum: If localMaxSum is greater, update globalMaxSum.
Result: The largest sum of a contiguous subarray is in globalMaxSum.
Efficiency: The time complexity is O(n).

xxxxxxxxxx
 
function solveMaxSubArrayProblem(input)
{
    var n = input.length
    var globalMaxSum = Number.MIN_VALUE
    var localMaxSum = 0
      
        for (var i = 0; i < n ; i++) {
            localMaxSum = Math.max(input[i],input[i]+localMaxSum)
            if(localMaxSum>globalMaxSum){
                globalMaxSum = localMaxSum
            }
​
        }
    return globalMaxSum
}
  
var input = [ 1, -2, 5, -3, 4, -1, 6 ]
var result = solveMaxSubArrayProblem(input)
document.write(result)

Let's test your knowledge. Click the correct answer from the options.

What is the time complexity to find the largest sum of a contiguous subarray using Kadene's algorithm?

Click the option that best answers the question.

O(n)
O(1)
O(log n)
None of the above

Conclusion: Mastering the Maximum Subarray Problem

In this enlightening journey, we delved into solving the Maximum Subarray Problem using the powerful Kadane's Algorithm. Here's a recap of what we covered:

Understanding the Problem

We started by unraveling a common challenge in computer science: finding the largest sum of contiguous elements in an array. It's a problem that might seem simple at first glance but holds fascinating complexity.

Introducing Kadane's Algorithm

Named after Joseph Born Kadane, this algorithm offers an optimal and elegant solution to the problem. Its beauty lies in the way it breaks down the complex task into manageable steps.

Exploring the Concept of "localMaxSum"

We focused on the essential concept of "localMaxSum," representing the maximum sum of a contiguous subarray ending at each specific index. By understanding how each local maximum builds upon the previous one, we discovered the algorithm's efficiency.

Insightful Observations

We took a deep dive into localMaxSum[3], uncovering how the algorithm builds solutions incrementally. This led to valuable insights, revealing a simple yet powerful relationship between consecutive local maximum sums and laying the groundwork for an optimal solution.

Implementing the Algorithm

We translated our understanding into practical code implementations across multiple programming languages. This hands-on approach provided a clear path to applying Kadane's Algorithm in real-world scenarios.

The Power of Incremental Solutions

Kadane's Algorithm is a shining example of how focusing on local, incremental solutions can lead to a global understanding. By solving small parts of the problem and building upon them, it offers an efficient and mathematically elegant approach.

One Pager Cheat Sheet

We're going to learn about Kadane's Algorithm and its implementation in Python, JavaScript, and Java, in order to solve the Maximum Subarray Problem.
Kadane's Algorithm is a form of Dynamic Programming developed by Joseph Born Kadane which provides an optimal solution for the Maximum Subarray Problem.
The Maximum Subarray Problem is to find the largest sum of a contiguous subarray in an input array of size n.
The Brute Force approach can be used to calculate the largest sum of a contiguous subarray in an array by comparing all possible subarrays and setting the max sum to a globalMaxSum variable, with a time complexity of O(n^2).
The time complexity of this algorithm is O(n²), as it requires two loops (outer loop with index i from 0 to n-1 and inner loop with index j from j set to i to n-1).
Kadene's Algorithm is an optimal approach with time complexity O(n), to the maximum subarray problem which is found by looping through the array, comparing the local Max Sums, and updating the global Max Sum at each iteration.
Kadene's Algorithm to find the largest sum of a contiguous subarray has a time complexity of O(n) due to its single loop iteration from index 0 to index n-1.
We solved the Maximum Subarray Problem in an optimal way using Kadene's Algorithm.

1) Kadane’s Algorithm at a Glance (Why this matters)

2) Meet the Maximum Subarray Problem (with a picture in your head)

3) Brute Force (the “try everything” approach)

4) Brute Force in Code (get it working first)

5) Kadane’s Algorithm (the elegant upgrade)

6) Kadane in Code (concise and fast)

What you’ll walk away with

Kadene's Algorithm Overview

Joseph Born Kadane and His Contribution

The Problem: Maximum Subarray

Dynamic Programming: Breaking It Down

How Kadane's Algorithm Works

Maximum Subarray Problem

Assumptions

Brute Force Approach

Try this exercise. Click the correct answer from the options.

Click the option that best answers the question.

Kadane's Algorithm - Unpacking an Optimal Solution

Introducing the Concept of "localMaxSum"

Exploring localMaxSum[3]

Possible Contiguous Subarrays

An Insightful Observation

The Insight's Significance

Implementing Kadane's Algorithm

Let's test your knowledge. Click the correct answer from the options.

Click the option that best answers the question.

Conclusion: Mastering the Maximum Subarray Problem

Understanding the Problem

Introducing Kadane's Algorithm

Exploring the Concept of "localMaxSum"

Insightful Observations

Implementing the Algorithm

The Power of Incremental Solutions

One Pager Cheat Sheet

Programming Categories

Popular Lessons