Kadane's Algorithm - Unpacking an Optimal Solution

To thoroughly understand Kadane's Algorithm, we'll examine an example array: [1, -2, 5, -3, 4, -1, 6]. Here's an illustrative representation:

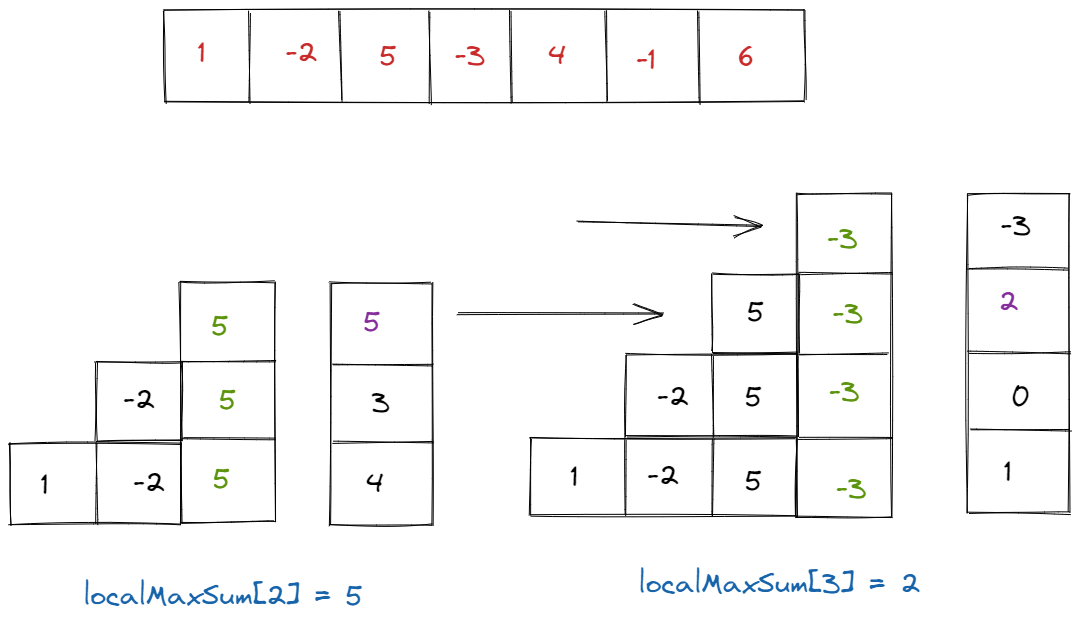
Introducing the Concept of "localMaxSum"

The key concept in Kadane's Algorithm is "localMaxSum," which represents the maximum sum of a contiguous subarray ending at a specific index. By keeping track of this "local" maximum, we can efficiently find the "global" maximum sum across the entire array.

Exploring localMaxSum[3]

Why are we looking at localMaxSum[3]? It's a pivotal point in understanding the algorithm. By examining this specific index, we can gain insights into how the algorithm builds solutions progressively. Let's break it down:

Possible Contiguous Subarrays

A "contiguous subarray" means a continuous sequence of elements within the array. For localMaxSum[3], the possible contiguous subarrays are:

• [-3] // index 3 only
• [5,-3] // index 2 & 3
• [-2,5,-3] // index 1, 2 & 3
• [1,-2,5,-3] // index 0, 1, 2 & 3

These combinations represent different ways to sum the elements ending at index 3. Among these, the combination [5,-3] sums up to 2, and therefore, the localMaxSum[3] is found to be 2.

An Insightful Observation

Now, let's compare localMaxSum[3] with localMaxSum[2]. What distinguishes them? It's only the element -3 at index 3. To find localMaxSum[3], we need the previous localMaxSum[2] and the element at index 3.

The Insight's Significance

This observation forms the heart of Kadane's Algorithm. It tells us that the localMaxSum at index i depends on only two factors: 1. The current element at index i. 2. The localMaxSum at the previous index i-1.

This relationship simplifies the problem significantly and leads to an efficient solution.

Implementing Kadane's Algorithm

Now, let's translate our understanding into practical steps and code:

1. Loop Through the Array: Iterate from index 0 to n-1.
2. Calculate localMaxSum: Use the formula:
   SNIPPET

   1localMaxSum[i] = max(input[i], input[i] + localMaxSum[i-1])

3. Compare with globalMaxSum: If localMaxSum is greater, update globalMaxSum.
4. Result: The largest sum of a contiguous subarray is in globalMaxSum.
5. Efficiency: The time complexity is O(n).

xxxxxxxxxx

function solveMaxSubArrayProblem(input)

{

    var n = input.length

    var globalMaxSum = Number.MIN_VALUE

    var localMaxSum = 0

        for (var i = 0; i < n ; i++) {

            localMaxSum = Math.max(input[i],input[i]+localMaxSum)

            if(localMaxSum>globalMaxSum){

                globalMaxSum = localMaxSum

            }

​

        }

    return globalMaxSum

}

var input = [ 1, -2, 5, -3, 4, -1, 6 ]

var result = solveMaxSubArrayProblem(input)

document.write(result)