AlgoDaily - Longest Increasing Subsequence

Good afternoon! Here's our prompt for today.

The Longest Increasing Subsequence (LIS) is a subsequence within an array of numbers with an increasing order. The numbers within the subsequence have to be unique and in an ascending manner. It's important to note that the items of the sequence do not have to be in consecutive locations within the array.

Can you write an efficient program that finds the length of Longest Increasing Subsequence, also called LIS?

Examples

Here are some examples and their solutions:

SNIPPET

1Input: {1,5,2,7,3}
2LIS = 3.  The longest increasing subsequence could be any of {1,5,7},{1,2,3},{1,2,7}
3
4Input: {13,1,3,4,8,4}
5LIS = 4.  The longest increasing subsequence {1,3,4,8}
6
7Input: {13,1,3,4,8,19,17,8,0,20,14}
8LIS = 6.  The longest increasing subsequence {1,3,4,8,17,20},{1,3,4,8,19,20}

Constraints

Length of the given array <= 100000
The array will always contain integer values between -1000000000 and 1000000000
Expected time complexity : O(nlogn)
Expected space complexity : O(n)

Try to solve this here or in Interactive Mode.

How do I practice this challenge?

xxxxxxxxxx
    'PASSED: ' + '`LISsolveDP([13,1,3,4,8,19,17,8,0,20,14])` should return `6`'
 
var assert = require('assert');
​
/**
 * Dynamic programming approach to find longest increasing subsequence.
 * Complexity: O(n * n)
 *
 * @param {number[]} arr
 * @return {number}
 */
​
function LISsolveDP(arr) {
  // Create an array for longest increasing substrings lengths and
  // fill it with 1s. This means that each element of the arr
  // is itself a minimum increasing subsequence.
  const lengthsArr = Array(arr.length).fill(1);
​
  let prevElIdx = 0;
  let currElIdx = 1;
​
  while (currElIdx < arr.length) {
    if (arr[prevElIdx] < arr[currElIdx]) {
      // If current element is bigger then the previous one. then
      // it is a part of increasing subsequence where length is
      // by 1 bigger then the length of increasing subsequence
      // for the previous element.
      const newLen = lengthsArr[prevElIdx] + 1;
      if (newLen > lengthsArr[currElIdx]) {
        // Increase only if previous element would give us a
        // bigger subsequence length then we already have for

Here's how we would solve this problem...

How do I use this guide?

How to Solve LIS

In this tutorial, I'll refer to the longest increasing subsequence as LIS. Let's first explore a simple recursive technique that can find the LIS for an array. We'll use the following notation to explain:

Suppose we have a function LIS(arr, n). Let this function reflect the length of the longest increasing sub-sequence that has arr[n] as "its last element".

We'll build on this function shortly. With this, let's look at the examples below. Here, all the subsequence indices start from zero. We're just exploring some patterns for now:

SNIPPET

1// in the below example, we're looking for arr[0], which is 1
2LIS({1,3,4,0}, 0) = 1        // the solution is the simple subsequence {1}
3
4// continuing the pattern
5// here we're looking for a subsequence ending in arr[1]
6LIS({1,3,4,0}, 1) = 2        // the subsequence {1,3} w/ length 2
7// further continuing..
8LIS({1,3,4,0}, 2) = 3        // the subsequence {1,3,4} w/ length 3
9LIS({1,3,4,0}, 3) = 1        // the subsequence {0} as it has to include arr[3]

Some observations emerge as we go through this exercise: as the subsequence has to end in arr[n], it can only include elements that satisfy two conditions:

The elements need to be at an index smaller than n.
The elements themselves must be smaller than arr[n] to fit the "increasing subsequence" condition.

We can thus derive the following rule from our observations:

SNIPPET

1LIS(arr, n) = 1 + max( LIS(arr, j) ) max computed over all j, 0<=j<n and arr[j]<arr[n]

We can translate this into plain English: if we can find LIS(arr, n) (the LIS with arr[n] as its last element) for all indices of the array, then the longest increasing subsequence for the entire array LISMax(arr) would be the maximum of all the LIS(arr, n), computed for all valid indices n:

SNIPPET

1LISMax(arr) = max( LIS(arr, n) ) max computed for all valid indices n of the array

Pseudo-Code

Now that we have a simple rule to solve the problem, let's write the pseudo-code for it. We've essentially broken the larger problem into subproblems (figuring out the LIS(arr, n) for multiple ns).

SNIPPET

1Routine: LISMax(arr)
2Input: array of size S
3Output: Length of longest increasing subsequence
4
5LISMax(arr)
6
71. max = 0
82. Loop from n = 0..(S-1)
9    a. Compute temp = LIS(arr, n)
10    b. if temp > max then max = temp
11return max

Alternatively, the pseudo-code for computing LIS with two parameters is given below:

SNIPPET

1Routine: LIS(arr, n)
2Input: array of size S and index n
3Output: Length of longest increasing subsequence that has arr[n] as its last item
4
5LIS(arr, n)
6
7Base case:
81. if (n==0) return 1
9
10Recursive case:
111. max = 1
122. Loop from j=0..(n-1)
13    a. if (arr[j]<arr[n])
14            i. compute temp = LIS(arr, j)
15            ii. if (temp>max) then max=temp
16return max

To understand how this pseudo-code works, here's an an example of LIS computation for {2, 3, 8, 5, 6} for index 4. At index 4 is the number 6, and thus, the subsequence has to include the number 6 as its last item.

In the below visual, we seek any numbers smaller than 6 to see if there is a potential increasing subsequence there. Follow the logic from top to bottom, and you'll see we find the solution from prior solutions, in a surprisingly similar manner to Fibonacci Sequence.

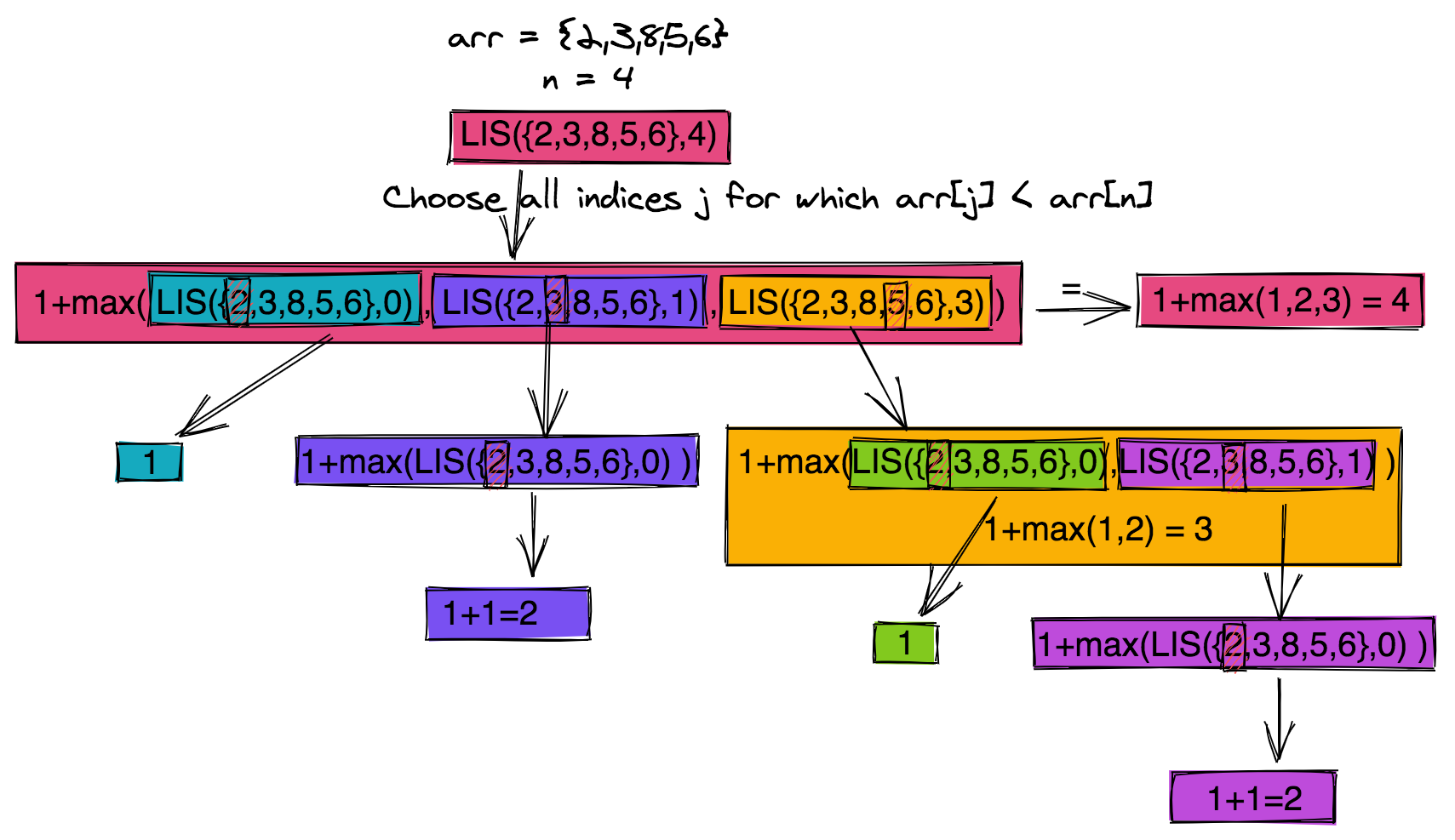
The figure shows that LIS(arr, 0) needs to be computed again and again. The same is the case for LIS(arr, 1). For larger values of n, there will be many values for which the function has to be repeated. This would lead to a time complexity of O(2^n), which is exponential. As computer scientists, we know that it is not a practical solution.

Dynamic Programming to the Rescue

The basic principle behind dynamic programming is that if your solution has a recursive structure, then you can:

Break down the problem into smaller repeating sub-problems.
Store the solutions of the sub-problems and use them later when needed

For example, LIS(arr, 0) and LIS(arr, 1) are re-calculated and required again and again. Alternatively, once computed, we can store them in an array, and use this result whenever it is needed.

Hence, now we have to account for an additional array. Let's call this array LISArr, which stores the value of LIS(arr, n) at index n.

Initialize each element of LISArr to zero.
If LIS(arr, n) is required, then check the value of LISArr[n].
1. If LISArr[n] is zero, then compute LIS(arr,n) and store in LISArr[n]
2. If LISArr[n] is greater than zero, then simply use its value from the array.

Now it is time to change the prior pseudo-code to incorporate dynamic programming. Only the LIS(arr, n) routine needs to be changed, with one additional parameter to include the array LISArr.

We can see that the time complexity of this pseudo-code is still quadratic, i.e., O(n^2). The LISDP function runs for each item of the array and for each item, LIS runs at the most n times. This makes the overall complexity O(n^2).

xxxxxxxxxx
 
Routine: LISDP(arr,n,LISArr)
Input: an array of size S and index n, length array same size as arr and initialized to zero
Output: Length of longest increasing subsequence that has arr[n] as its last item
​
LISDP(arr,n,LISArr)
​
Base case:
1. if (n==0) return 1
2. if LISArr[n] != 0 return LISArr[n]  //do not go in the recursive case
​
Recursive case:
1. max = 1
2. Loop from j=0..(n-1)
    a. if (arr[j]<arr[n])
        i.   LISArr[j] = LISDP(arr,j,LISArr) //compute LIS(arr,j)
        ii. if (LISArr[j] > max) then max = LISArr[j]
return max

Code for LIS using Dynamic Programming

Finally, here's the code for implementing LIS using dynamic programming in a few different languages. As always, we advise you to work everything out on a piece of paper before implementing anything.

xxxxxxxxxx
 
// Dynamic programming solution
const longestIncreasingSubsequence = function (nums) {
  // Create an array to memoize
  const dpMemo = Array.from(nums, () => 1);
  // Initialize subsequence length
  let max = 1;
  // Check all increasing subsequences up to the current ith number in nums
  for (let i = 1; i < nums.length; i++) {
    // Keep track of subsequence length in the dpMemo array
    for (let j = 0; j < i; j++) {
      // Only change dpMemo value if the numbers are increasing
      if (nums[i] > nums[j]) {
        // Set the value to be the larget subsequence length
        dpMemo[i] = Math.max(dpMemo[i], dpMemo[j] + 1);
        // Check if this subsequence is the largest
        max = Math.max(dpMemo[i], max);
      }
    }
  }
  return max;
};
​
const result = longestIncreasingSubsequence([
  5, 15, 8, 7, 4, 10, 20, 19, 7, 25, 29, 11,
]);
console.log(result);

An Efficient Algorithm for Running LIS

LIS using dynamic programming still requires O(n^2) computations. Can you find an improved algorithm that uses O(n log n) time?

To understand how the solution of finding LIS can be made more efficient, let's review binary search first. We can improve upon the computation time by making use of the fact that it takes O(log n) time to search for an item in a sorted array when using binary search.

Coming back to finding LIS-- we'll use an intermediate array again called LISArray. Let us define its purpose in this instance, and highlight a few important points:

We will use LISArray to store indices of the input array arr.
We'll also use LISArray to keep track of the longest subsequence found so far.
LISArray[j]: LISArray[j] will map to the index of the smallest item of arr that's the last item for a subsequence of length j.
arr[LISArray[j]]: Ending element of subsequence of length j.
Size of LISArray[j] = (Size of arr)+ 1, as LISArr[j] has information on subsequence of length j, indices start at zero so we need an additional element to store the maximum possible length.
LISArray[0] is unused.
Maximum index of LISArray can be at (Size of arr).

Purpose of the Array

Once we understand the purpose of the array LISArray, the algorithm itself is pretty easy to understand. In the examples below, LISArray's indices are a result from scanning the entire input arr. Note that at index j, it is storing the result of the smallest element in the entire array that occurs at the end of a subsequence of length j.

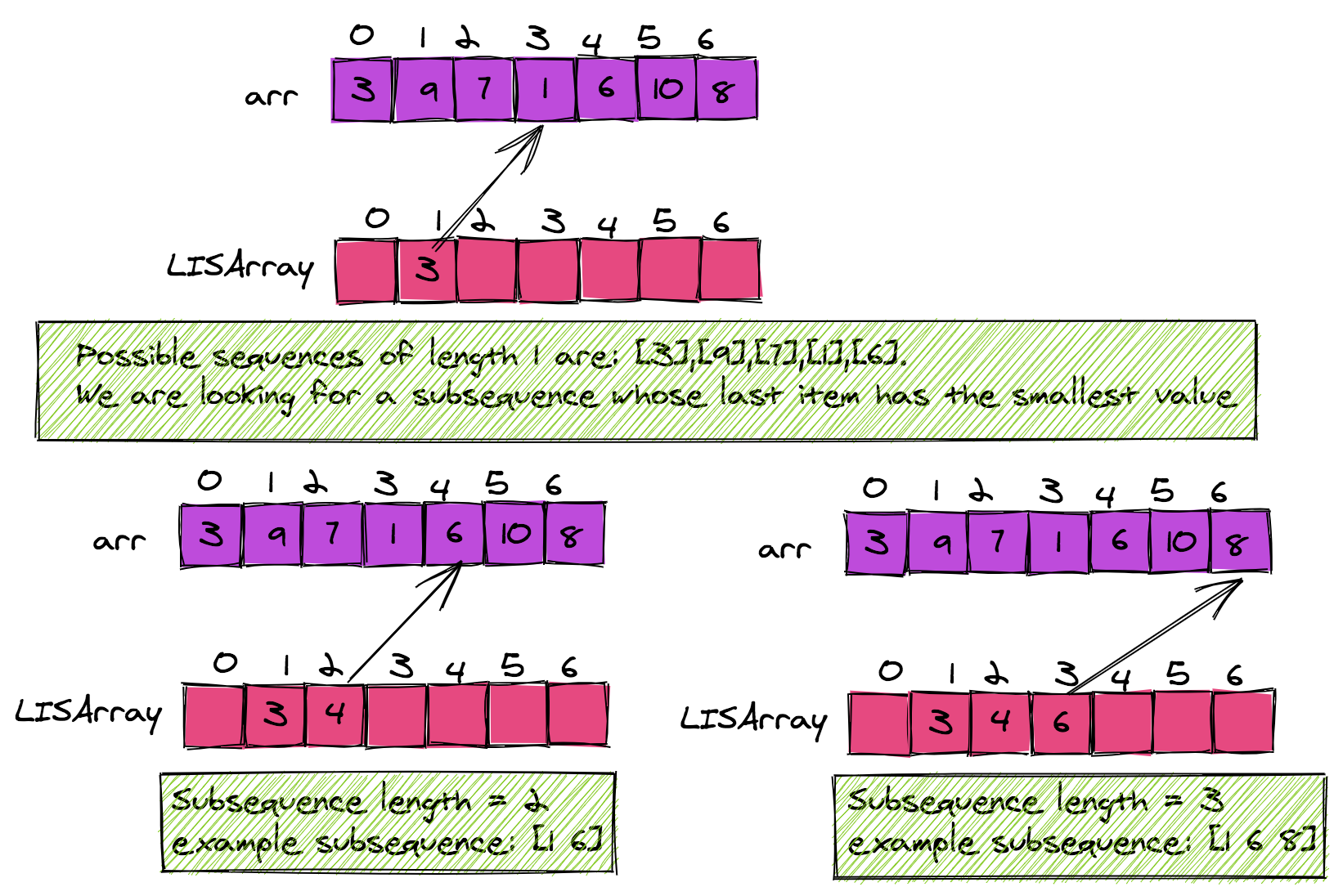
This is interesting because note the following;

SNIPPET

1LISArray: {3, 4, 8}
2arr[LISArray[i]] = 1, 6, 8     // (for i=1..2)

So the important point to note is that LISArray stores the indices of the items of input array in sorted order!

Hence the following is true:

SNIPPET

1    arr[LISArray[1]] < arr[LISArray[2]] < arr[LISArray[3]] < arr[LISArray[4]] ...
2    arr[LISArray[j]] < arr[LISArray[j+1]]

Ready for Pseudo-Code

Armed with this knowledge, we are ready to construct the pseudo-code for an algorithm that solves LIS efficiently.

All we need to do is scan the items of arr one by one, and find their place in LISArray. Because LISArray stores the indices of items of the input array in sorted order, we can use binary search to find the place of arr[i] in LISArray.

The example below shows how LISArray is filled out one by one, when given an element of arr. We also need to keep track of the last filled index of LISArray. We only add a new item to LISArray when the next item of arr is higher than all items that were previously added.

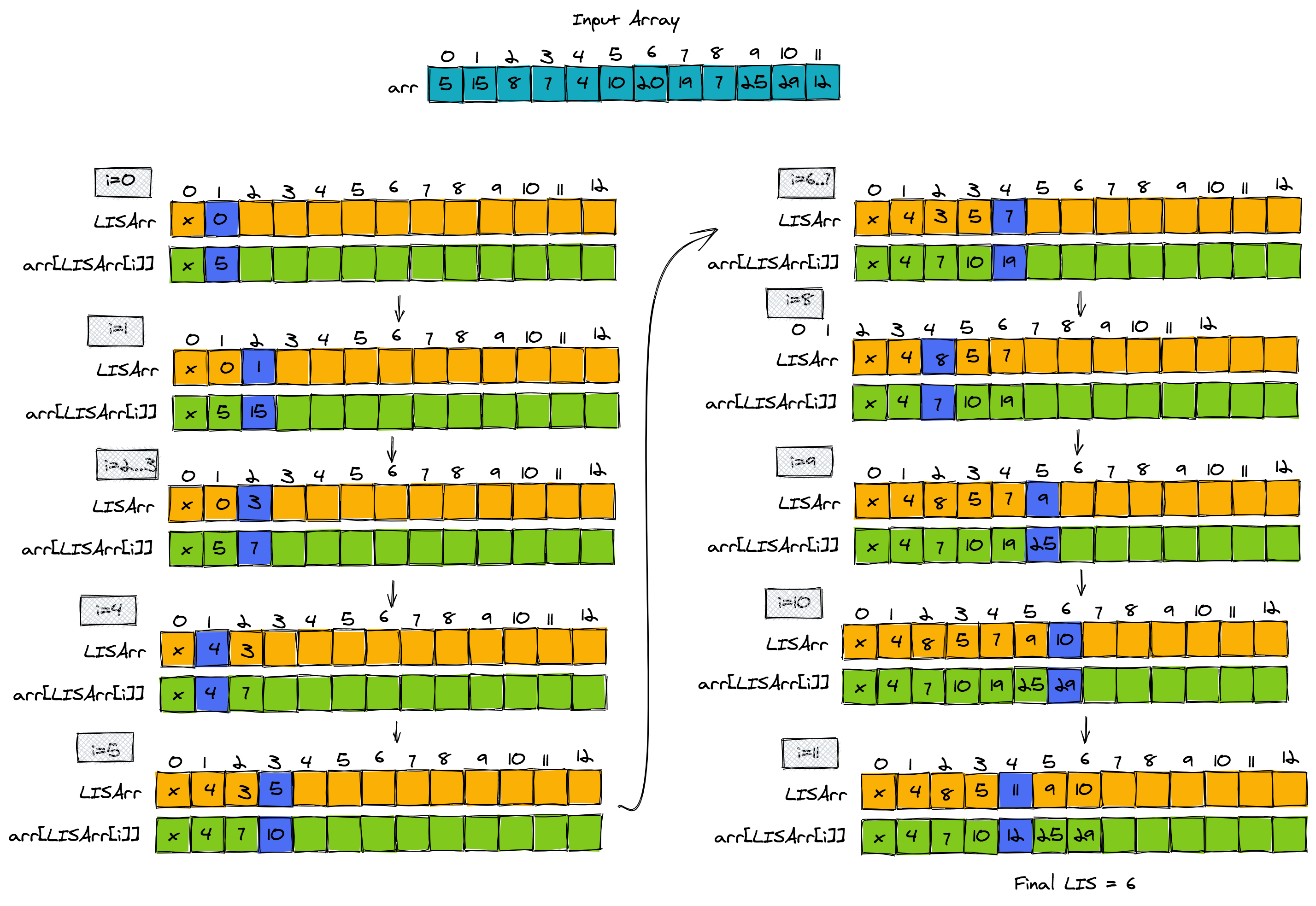
The final pseudo-code is given below. Note that the algorithm goes through each item of arr exactly once (n items scanned once) and finds their place in LISArray using binary search (O(log n) time). Hence the overall time complexity of this algorithm is O(n log n).

SNIPPET

1Routine: LISFast
2Input: arr of length n
3Output: Largest increasing subsequence within arr
4Intermediate storage: LISArray of size (n+1), initialized to zero
5
61. lastIndex = 1
72. LISArr[lastIndex] = 0
83. for i=1..n
9    a. ind = binary search for index position in LISArr for arr[i]
10    b. LISArr[ind] = i
11    c. if (ind > lastIndex)
12        lastIndex = ind
134. return lastIndex

You can now write efficient code for finding LIS in O(n log(n)) time using the examples and pseudo-code.

Getting the sequence along with the length

Ever wondered how you can get the actual sequence from the given array? We can do this easily by using another array. Try to edit the above solution and solve this one. Finally, see the solution attached.

xxxxxxxxxx
console.log(getLIS([5, 1, 8, 10, 5, 2, 14, 17, 19, 7, 9, 29]));
 
function getLIS(nums) {
  // Check if the sequence is empty
  if (!nums) {
    return nums;
  }
​
  const M = [];
  const P = [];
​
  // We know that there is at least an increasing subsequence of length one
  // which is the first element
  let L = 1;
  M[0] = 0;
​
  // So we try to increase the length L from second item.
  for (let i = 1; i < nums.length; i++) {
    // We do a binary search just like the previous solution
    let left = 0;
    let right = L;
​
    // Check the right bound
    if (nums[M[right - 1]] < nums[i]) {
      j = right;
    } else {
      while (right - left > 1) {
        mid = Math.floor((right + left) / 2);
        if (nums[M[mid - 1]] < nums[i]) {
          left = mid;
        } else {

One Pager Cheat Sheet

An efficient program that can find the length of the Longest Increasing Subsequence (LIS) should satisfy the constraints of O(nlogn) time complexity and O(n) space complexity.
We can use a recursive algorithm to compute the length of the LIS for an array, which is the maximum of LIS(arr, n) for all the valid indices n of the array.
A pseudo-code is written to compute the Length of Longest Increasing Subsequence in an array using recursive cases and base cases, which helps to reduce the time complexity to O(2^n).
Dynamic Programming can be used to break down a problem into smaller repeating sub-problems and significantly reduce the time complexity from O(n^2) to O(n) by storing the solutions of the sub-problems and using them later when needed.
Implementing Longest Increasing Subsequence (LIS) using Dynamic Programming may be accomplished by following the steps outlined and working through examples on paper, before coding it in any language.
LISArray stores the indices of the items of the input array in sorted order, allowing for the comparison of elements at specified indices in the original array.
Armed with this knowledge, we are now ready to construct an O(n log n) algorithm for solving LIS efficiently.

This is our final solution.

To visualize the solution and step through the below code, click Visualize the Solution on the right-side menu or the VISUALIZE button in Interactive Mode.

xxxxxxxxxx
}
 
var assert = require('assert');
​
/**
 * Dynamic programming approach to find longest increasing subsequence.
 * Complexity: O(n * n)
 *
 * @param {number[]} arr
 * @return {number}
 */
​
function LISsolveDP(arr) {
  // Create an array for longest increasing substrings lengths and
  // fill it with 1s. This means that each element of the arr
  // is itself a minimum increasing subsequence.
  const lengthsArr = Array(arr.length).fill(1);
​
  let prevElIdx = 0;
  let currElIdx = 1;
​
  while (currElIdx < arr.length) {
    if (arr[prevElIdx] < arr[currElIdx]) {
      // If current element is bigger then the previous one. then
      // it is a part of increasing subsequence where length is
      // by 1 bigger then the length of increasing subsequence
      // for the previous element.
      const newLen = lengthsArr[prevElIdx] + 1;
      if (newLen > lengthsArr[currElIdx]) {
        // Increase only if previous element would give us a
        // bigger subsequence length then we already have for
        // current element.
        lengthsArr[currElIdx] = newLen;
      }

That's all we've got! Let's move on to the next tutorial.

If you had any problems with this tutorial, check out the main forum thread here.

Examples

Constraints

Try to solve this here or in Interactive Mode.

Here's how we would solve this problem...

How to Solve LIS

Pseudo-Code

Dynamic Programming to the Rescue

Code for LIS using Dynamic Programming

An Efficient Algorithm for Running LIS

Purpose of the Array

Ready for Pseudo-Code

Getting the sequence along with the length

One Pager Cheat Sheet

This is our final solution.

That's all we've got! Let's move on to the next tutorial.

Programming Categories

Popular Lessons