Ready for Pseudo-Code

Armed with this knowledge, we are ready to construct the pseudo-code for an algorithm that solves LIS efficiently.

All we need to do is scan the items of arr one by one, and find their place in LISArray. Because LISArray stores the indices of items of the input array in sorted order, we can use binary search to find the place of arr[i] in LISArray.

The example below shows how LISArray is filled out one by one, when given an element of arr. We also need to keep track of the last filled index of LISArray. We only add a new item to LISArray when the next item of arr is higher than all items that were previously added.

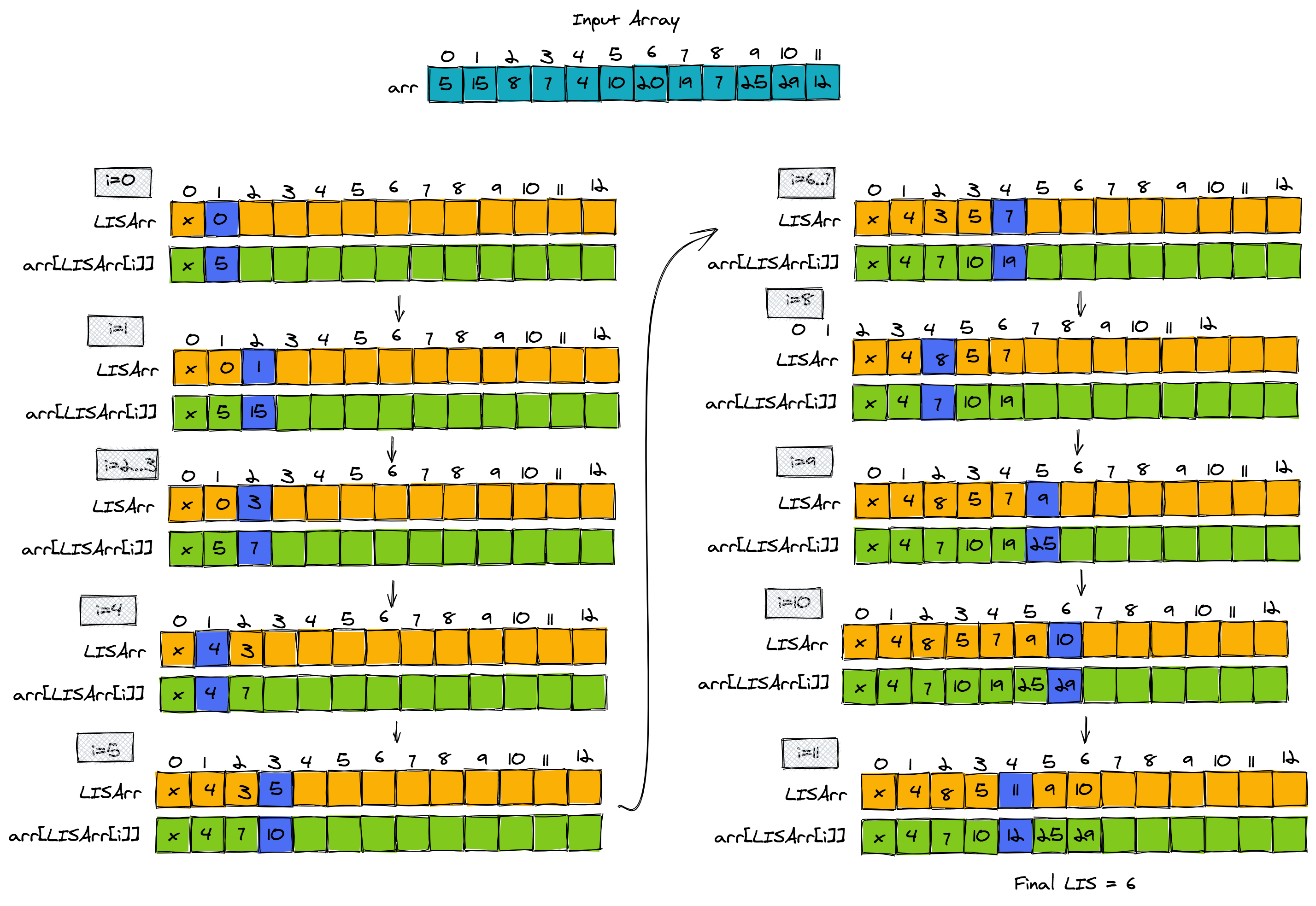
The final pseudo-code is given below. Note that the algorithm goes through each item of arr exactly once (n items scanned once) and finds their place in LISArray using binary search (O(log n) time). Hence the overall time complexity of this algorithm is O(n log n).

1Routine: LISFast
2Input: arr of length n
3Output: Largest increasing subsequence within arr
4Intermediate storage: LISArray of size (n+1), initialized to zero
5
61. lastIndex = 1
72. LISArr[lastIndex] = 0
83. for i=1..n
9    a. ind = binary search for index position in LISArr for arr[i]
10    b. LISArr[ind] = i
11    c. if (ind > lastIndex)
12        lastIndex = ind
134. return lastIndex

You can now write efficient code for finding LIS in O(n log(n)) time using the examples and pseudo-code.

Getting the sequence along with the length

Ever wondered how you can get the actual sequence from the given array? We can do this easily by using another array. Try to edit the above solution and solve this one. Finally, see the solution attached.

xxxxxxxxxx

console.log(getLIS([5, 1, 8, 10, 5, 2, 14, 17, 19, 7, 9, 29]));

function getLIS(nums) {

  // Check if the sequence is empty

  if (!nums) {

    return nums;

  }

​

  const M = [];

  const P = [];

​

  // We know that there is at least an increasing subsequence of length one

  // which is the first element

  let L = 1;

  M[0] = 0;

​

  // So we try to increase the length L from second item.

  for (let i = 1; i < nums.length; i++) {

    // We do a binary search just like the previous solution

    let left = 0;

    let right = L;

​

    // Check the right bound

    if (nums[M[right - 1]] < nums[i]) {

      j = right;

    } else {

      while (right - left > 1) {

        mid = Math.floor((right + left) / 2);

        if (nums[M[mid - 1]] < nums[i]) {

          left = mid;

        } else {