Pseudo-Code

Now that we have a simple rule to solve the problem, let's write the pseudo-code for it. We've essentially broken the larger problem into subproblems (figuring out the LIS(arr, n) for multiple ns).

1Routine: LISMax(arr)
2Input: array of size S
3Output: Length of longest increasing subsequence
4
5LISMax(arr)
6
71. max = 0
82. Loop from n = 0..(S-1)
9    a. Compute temp = LIS(arr, n)
10    b. if temp > max then max = temp
11return max

Alternatively, the pseudo-code for computing LIS with two parameters is given below:

1Routine: LIS(arr, n)
2Input: array of size S and index n
3Output: Length of longest increasing subsequence that has arr[n] as its last item
4
5LIS(arr, n)
6
7Base case:
81. if (n==0) return 1
9
10Recursive case:
111. max = 1
122. Loop from j=0..(n-1)
13    a. if (arr[j]<arr[n])
14            i. compute temp = LIS(arr, j)
15            ii. if (temp>max) then max=temp
16return max

To understand how this pseudo-code works, here's an an example of LIS computation for {2, 3, 8, 5, 6} for index 4. At index 4 is the number 6, and thus, the subsequence has to include the number 6 as its last item.

In the below visual, we seek any numbers smaller than 6 to see if there is a potential increasing subsequence there. Follow the logic from top to bottom, and you'll see we find the solution from prior solutions, in a surprisingly similar manner to Fibonacci Sequence.

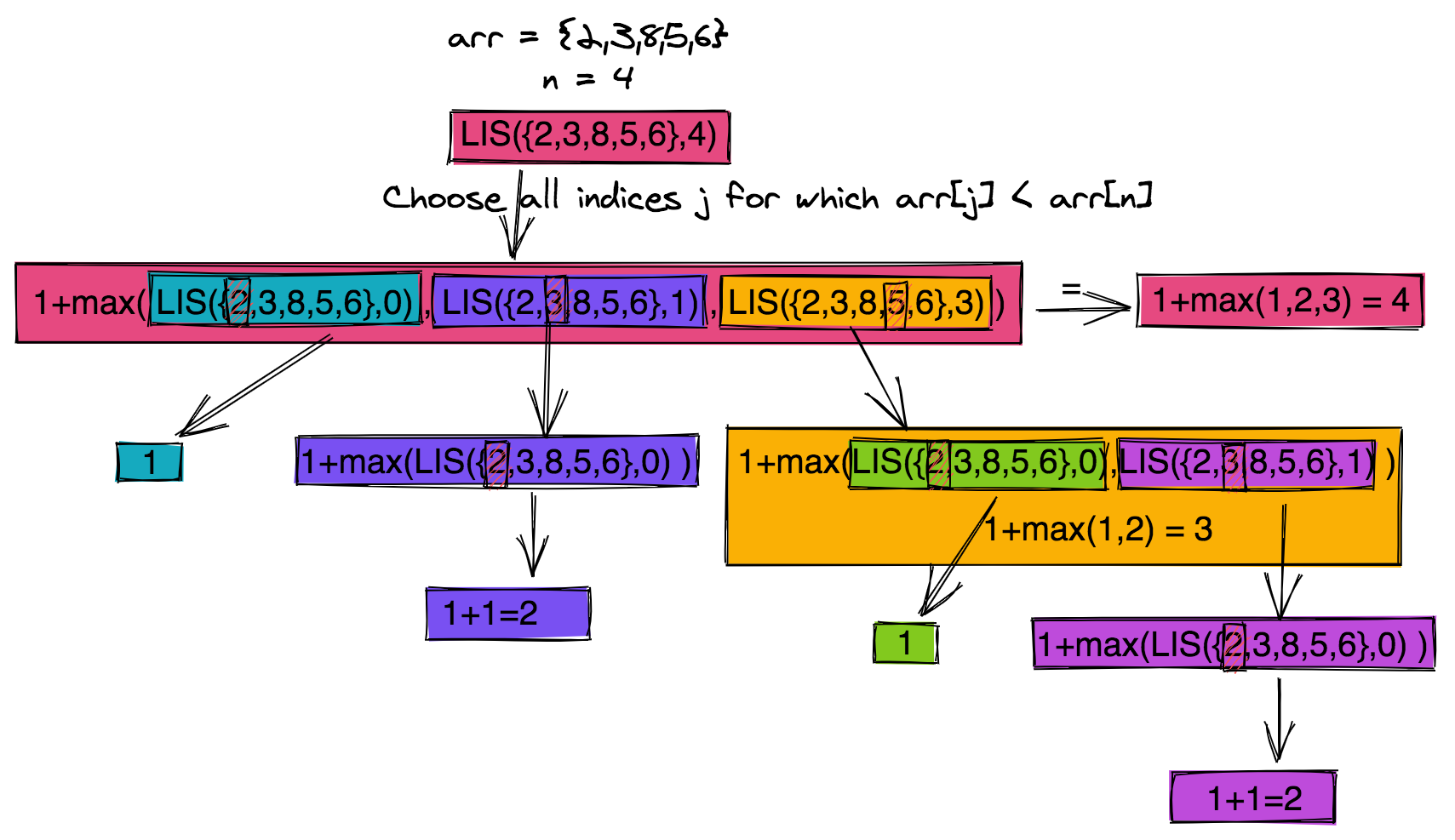
The figure shows that LIS(arr, 0) needs to be computed again and again. The same is the case for LIS(arr, 1). For larger values of n, there will be many values for which the function has to be repeated. This would lead to a time complexity of O(2^n), which is exponential. As computer scientists, we know that it is not a practical solution.