Brute Force Approach

The simplest solution to the problem is using the Brute Force approach:

• Find all the possible contiguous subarrays.
• Calculate their sum.
• Find the maximum of all the sums.

Now going back to our input array to understand the Brute Force solution to the problem:

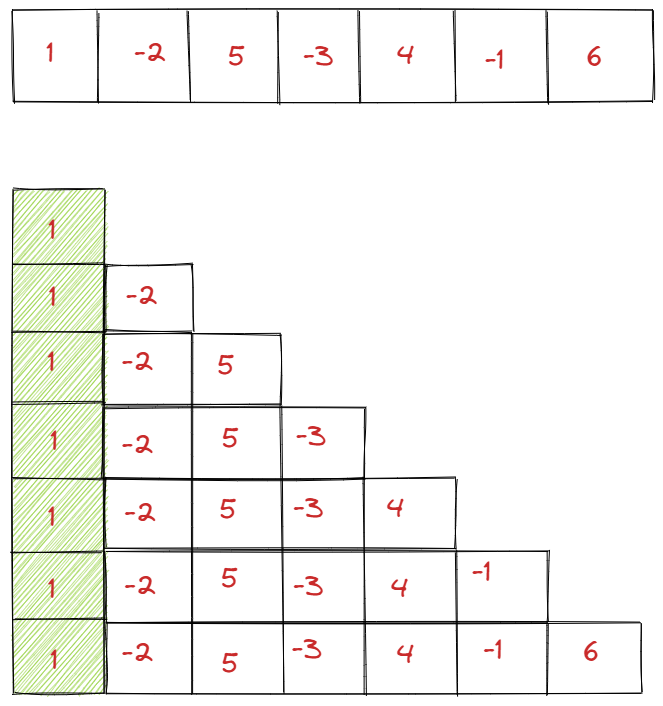
• This approach will require two loops.
• An outer loop with index i that will iterate from 0 to n-1.
• An inner loop with index j that will iterate from j set to i to n-1.
• The inner loop will calculate subArraySum:

1subArraySum = subArraySum + input[j]

• Meanwhile, subArraySum will be compared with globalMaxSum.
• If globalMaxSum will be less than subArraySum, then globalMaxSum will be set to subArraySum.
• In the end, we'll be able to find out the largest sum of a contiguous subarray.
• Note that the time complexity for this algorithm is O(n²)

Now heading to implementation in code to get a clearer understanding:

xxxxxxxxxx

function solveMaxSubArrayProblem(input)

{

    var n = input.length

    var globalMaxSum = Number.MIN_VALUE

    var subArraySum

        for (var i = 0; i < n ; i++) {

            subArraySum= 0;

            for (var j = i; j < n; j++) {

            subArraySum+= input[j]

            if (subArraySum> globalMaxSum) {

                globalMaxSum = subArraySum

            }

            }

        }

    return globalMaxSum

}

var input = [ 1, -2, 5, -3, 4, -1, 6 ]

var result = solveMaxSubArrayProblem(input)

document.write(result)