Good evening! Here's our prompt for today.
A perfect square is a number made by squaring a whole number.
Some examples include 1, 4, 9, or 16, and so on -- because they are the squared results of 1, 2, 3, 4, etc. For example:
11^2 = 1
22^2 = 4
33^2 = 9
44^2 = 16
5...However, 15 is not a perfect square, because the square root of 15 is not a whole or natural number.
| Perfect Square | Factors |
|---|---|
| 1 | 1 * 1 |
| 4 | 2 * 2 |
| 9 | 3 * 3 |
| 16 | 4 * 4 |
| 25 | 5 * 5 |
| 36 | 6 * 6 |
| 49 | 7 * 7 |
| 64 | 8 * 8 |
| 81 | 9 * 9 |
| 100 | 10 * 10 |
Given some positive integer n, write a method to return the fewest number of perfect square numbers which sum to n.
The follow examples should clarify further:
1var n = 28
2howManySquares(n);
3// 4
4// 16 + 4 + 4 + 4 = 28, so 4 numbers are requiredOn the other hand:
1var n = 16
2howManySquares(n);
3// 1
4// 16 itself is a perfect square
5// so only 1 perfect square is requiredConstraints
n<=10000nwill always be non zero positive integer- Expected time complexity :
O(n*sqrt(n)) - Expected space complexity :
O(n)
Try to solve this here or in Interactive Mode.
How do I practice this challenge?
xxxxxxxxxxfrom math import sqrt, ceildef howManySquares(n): # fill in return nimport unittestclass Test(unittest.TestCase): def test_1(self): assert howManySquares(16) == 1 print("PASSED: howManySquares(16) should return 1") def test_2(self): assert howManySquares(1) == 1 print("PASSED: howManySquares(1) should return 1") def test_3(self): assert howManySquares(966) == 3 print("PASSED: howManySquares(966) should return 3")if __name__ == "__main__": unittest.main(verbosity=2) print("Nice job, 3/3 tests passed!")Here's our guided, illustrated walk-through.
How do I use this guide?
Build your intuition. Is this statement true or false?
The perfect squares are the squares of the whole numbers: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100
Press true if you believe the statement is correct, or false otherwise.
We need to find the least number of perfect squares that sum up to a given number. With problems like this, the brute-force method seems to lean towards iterating through all the possible numbers and performing some operation at each step.
It seems from the get-go that we'll need to find all the perfect squares available to us before we reach the specified number in an iteration.
This means if the number is 30, we'll start at 1, then 2, and conduct a logical step at each number. But what logic do we need? Well, if we're given a number-- say, 100, how would we manually solve this problem and find the perfect squares that sum up to 100?
Like we said, we'd probably just start with 1 and get its perfect square. Then we'll move on to 2, and get the perfect square of 4. But in this case, we'll keep summing as we calculate each square. Mathematically speaking, it would look like:
xxxxxxxxxx// while (1*1) + (2*2) + (3*3) + (4*4) + ... <= 100Try this exercise. Fill in the missing part by typing it in.
What line below would give us the proper count?
1class Main {
2 public static int howManySquares(int num) {
3 int count = 0;
4
5 for (int i = 1; i <= num; i++)
6
7 // Is current number 'i' a perfect square?
8 for (int j = 1; j * j <= i; j++)
9 if (j * j == i)
10 _______________________
11
12 return count;
13 }
14
15 public static void main(String args[]) {
16 this.howManySquares(4);
17 }
18}Write the missing line below.
Our brute force solution isn't very optimal, so let's try to make it more efficient. At the very least, notice how we can limit our number of perfect squares to just the ones that are less than our number, since larger ones (in this case, greater than 100) wouldn't make sense. That reduces the time necessary to a degree.
So if we were looking for all the perfect squares that sum up to 12, we wouldn't want to consider 16 or 25-- they're too large for our needs.
To translate this into code, given our previous example, we'd essentially iterate through all numbers smaller than or equal to 100. At each iteration, we'd see if we can find a perfect square that is larger to "fit in" to the "leftover space".
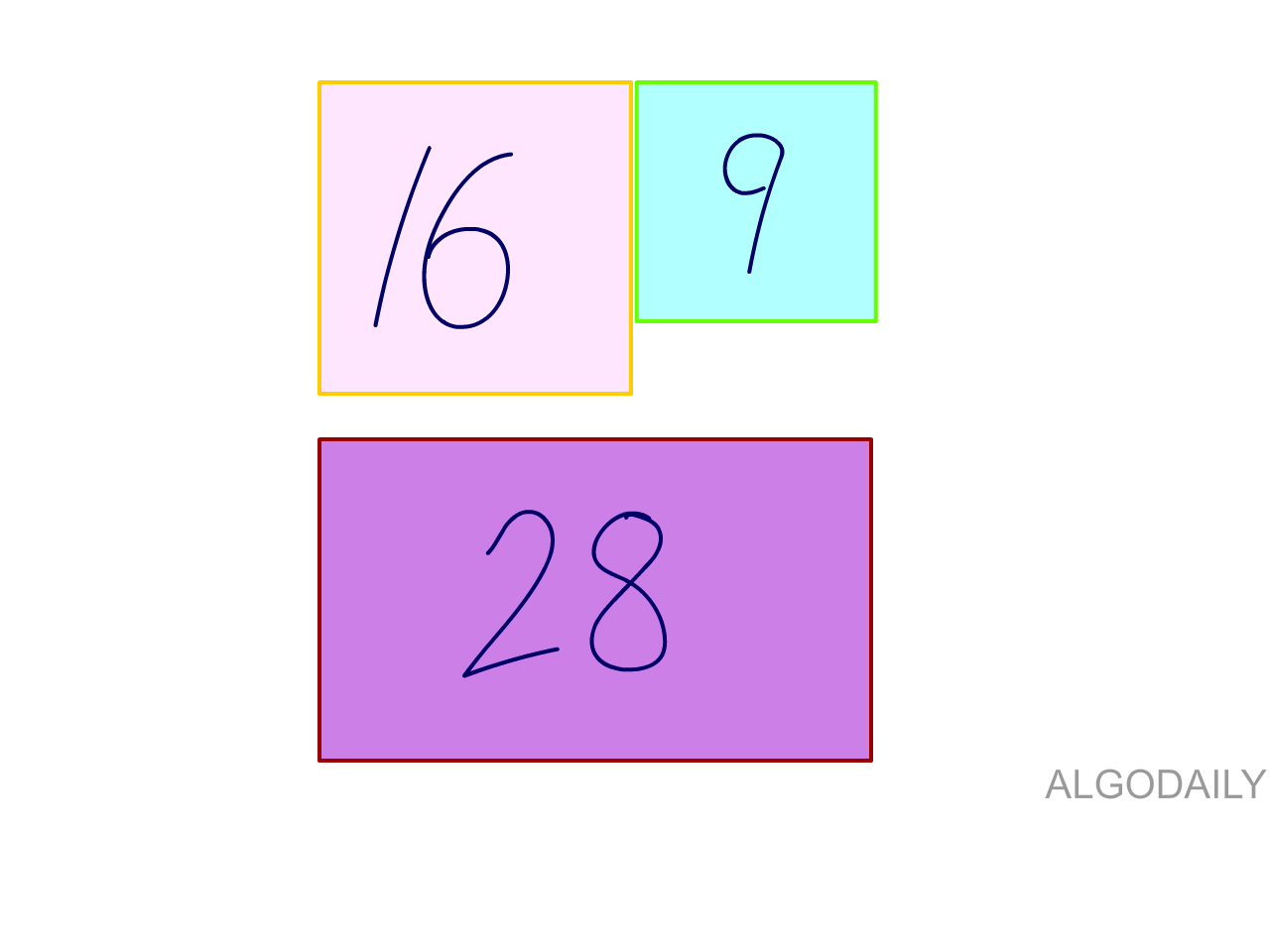
Picture these steps. Start with 28:

Try 16:

Cool, it fits-- let's keep 16. Try 9:
That also fits. What works with 16 and 9?
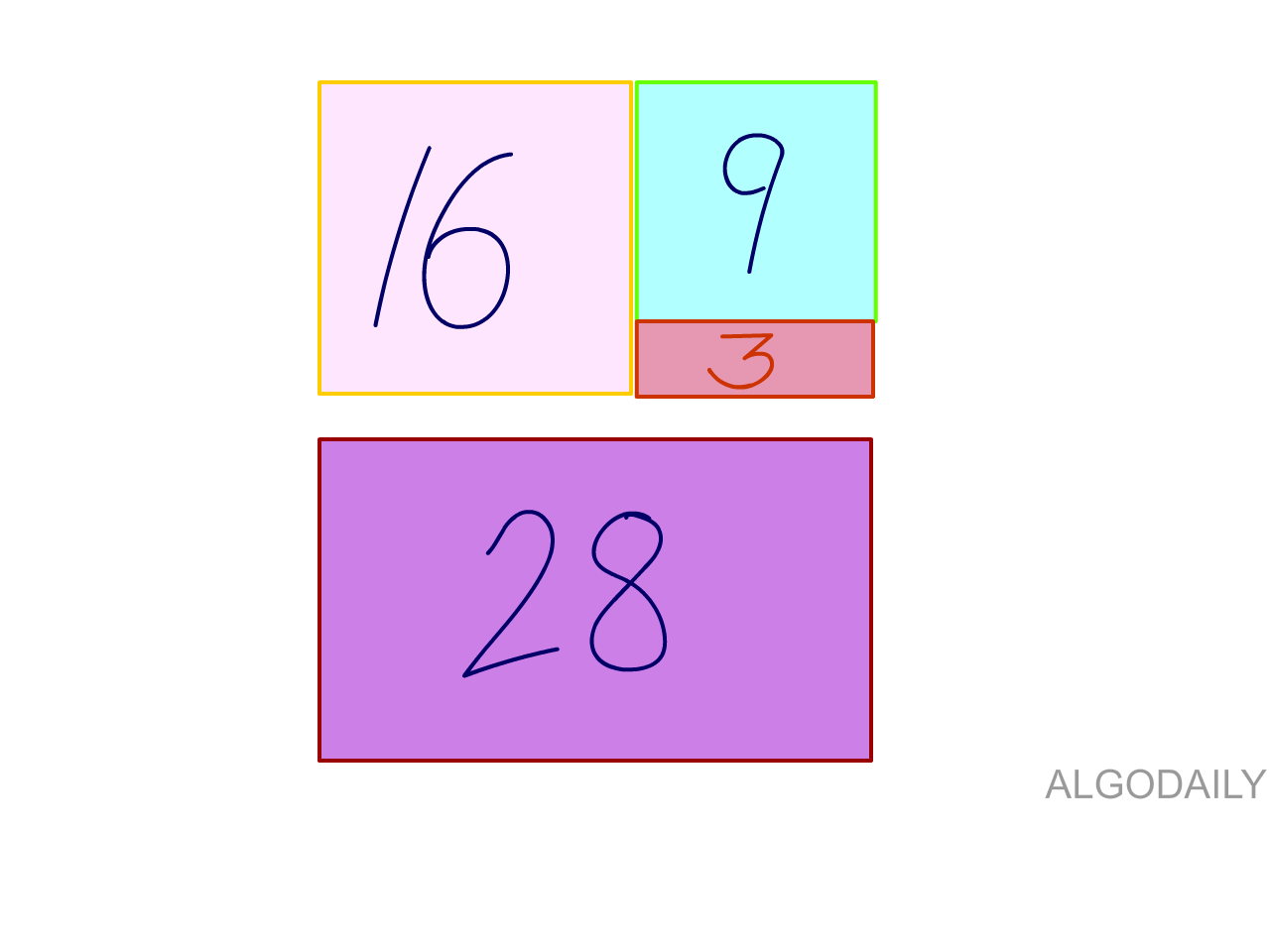
That won't work-- we can only fit 3 but it's not a perfect square. What else fits with 16?

OK, 4 works, and is a perfect square. Notice that it not only matches both conditions (fits and is a perfect square), but we can fit 3 of them in!
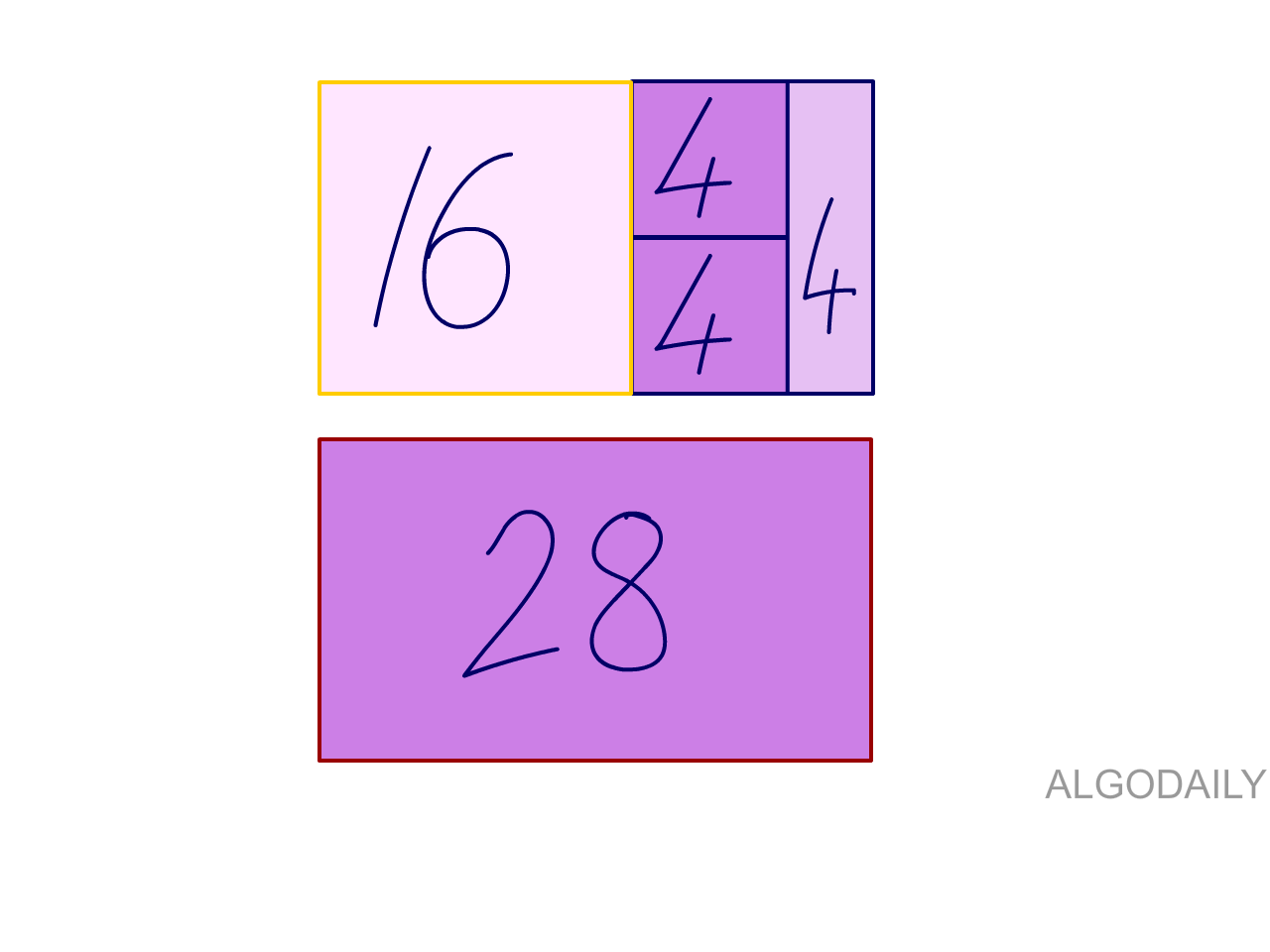
Given that approach, here's the logic translated to code. Read the comments carefully for clarification:
xxxxxxxxxxfunction howManySquares(num) { if (num <= 3) { return num; } result = num; for (let i = 1; i < num + 1; i++) { // get squared number temp = i * i; if (temp > num) { break; } else { // get whatever is lower: // 1 - the current minimum, or // 2 - the minimum after considering the next perfect square result = Math.min(result, 1 + howManySquares(num - temp)); } } return result;}console.log(howManySquares(16));The above, however, has an exponential time complexity-- that is, O(2^n). Additionally, we don't want to find all the possible perfect squares each time, that wouldn't be very time efficient.
How can we turn this into a shortest path problem? Notice the branching, too-- how might we construct a graph to help us work backwards from a sum to perfect squares? Additionally, there's the opportunity for reuse of calculations.
Well, if we used a data structure for storing the calculations-- let's say a hash, we can memo-ize the calculations. Let's imagine each key in the hash representing a number, and its corresponding value as being the minimum number of squares to arrive at it.
Alternatively, we can use an array, and simply store the sequence of perfect squares for easy lookup.
One Pager Cheat Sheet
- Perfect squares are numbers that result from squaring a whole number and can be used to find the fewest number of perfect squares that sum to a given number n, subject to the constraints of
nbeing a nonzero positive integer less than or equal to10000, and the expected time/space complexity beingO(n*sqrt(n))/O(n), respectively. - A number is a perfect square when its square root is a whole number, such as the 1st to 10th
perfect squares, which are1, 4, 9, 16, 25, 36, 49, 64, 81, 100. - We need to iterate through all possible numbers and perform a logical step at each step to find the least number of perfect squares that sum up to a given number.
- The
forloop will check each number from 1 up to the given number to see if it is a perfect square andcountis incremented by 1 for each perfect square found. - We can reduce our brute force solution to be more efficient by considering only perfect squares that are less than our target number, and iterating through these to sum them up to the target.
- We can optimize the time complexity of finding the minimum number of perfect squares needed to add up to a certain sum by turning it into a shortest path problem, constructing a
graphand memo-izing the calculations with ahashor anarray.
This is our final solution.
To visualize the solution and step through the below code, click Visualize the Solution on the right-side menu or the VISUALIZE button in Interactive Mode.
xxxxxxxxxx print("Nice job, 3/3 tests passed!")from math import sqrtdef howManySquares(n): # return n if it is less than or equal to 3, for n >= 0 if n <= 3: return n # create a dynamic table to store sequence dp = list(range(n + 1)) for i in range(4, n + 1): # loop until that number from 4 # loop through all small numbers to find minimum for x in range(1, int(sqrt(i)) + 1): # get the minimum squares required # by looking up in dp table dp[i] = min(dp[i], 1 + dp[i - x * x]) return dp[n]import unittestclass Test(unittest.TestCase): def test_1(self): assert howManySquares(16) == 1 print("PASSED: howManySquares(16) should return 1") def test_2(self): assert howManySquares(1) == 1 print("PASSED: howManySquares(1) should return 1")That's all we've got! Let's move on to the next tutorial.
If you had any problems with this tutorial, check out the main forum thread here.

