Good evening! Here's our prompt for today.

The Trapping Rain Water Challenge: A Deep Dive

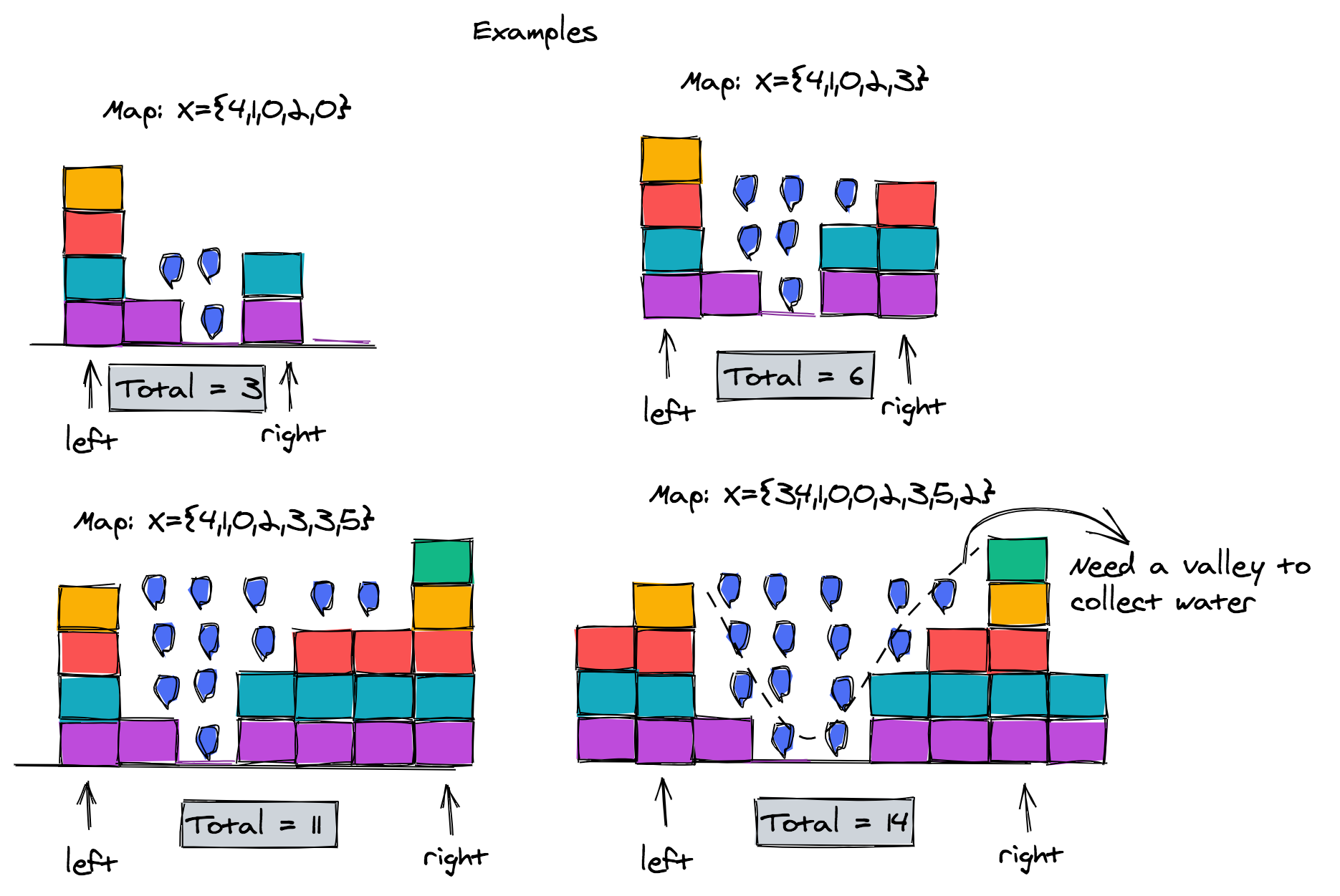
Imagine you're looking at an elevation map displaying rainfall over a region's landscape. The map consists of bars of varying heights, each representing different elevations. Can you determine the amount of rainwater that this uneven terrain can hold?

Problem Setup

We'll simplify the problem by using a one-dimensional array of non-negative integers. Each integer represents the height of the land at different points. The objective is to calculate the volume of rainwater that can be trapped by this series of elevations.

To better visualize this, consider the diagram below, which illustrates various elevation maps and the potential rainwater they can hold. Think of it like a game of Tetris; we aim to find how many units of rainwater could be accommodated in the available gaps.

Constraints and Performance Metrics

• Length of the array <= 100000
• Values in the array >=0
• The final answer would fit in the Integer range(< 2^32)
• Expected time complexity : O(n)
• Expected space complexity : O(1)

Try to solve this here or in Interactive Mode.

How do I practice this challenge?

xxxxxxxxxx

​

def trap(bars):

    # fill in

    pass

​

​

# Trapping Rain Water within given set of bars

if __name__ == "__main__":

    heights = [5, 1, 2, 4, 4, 4, 3, 1, 0, 0, 0]

    print("Maximum amount of water that can be trapped is", trap(heights))

​

​

import unittest

​

​

class Test(unittest.TestCase):

    def test_1(self):

        assert trap([0, 0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1, 0, 0]) == 6

        print("PASSED: `trap([0,0,1,0,2,1,0,1,3,2,1,2,1,0,0])` should return `6`")

​

    def test_2(self):

        assert trap([0, 0, 1, 0, 2, 4, 4, 4, 2, 3, 1, 0, 2, 4, 3, 1, 0, 1]) == 14

        print(

            "PASSED: `trap([0,0,1,0,2,4,4,4,2,3,1,0,2,4,3,1,0,1])` should return `14`"

        )

​

    def test_3(self):

        assert trap([0, 0, 1, 2, 4, 4, 4, 3, 1, 0, 0, 0]) == 0

        print("PASSED: `trap([0,0,1,2,4,4,4,3,1,0,0,0])` should return `0`")

​

Here's our guided, illustrated walk-through.

How do I use this guide?

As usual, we'll solve this by examining some test cases to get a feel for the varying scenarios. After we've developed an intuition, we can try to identify a pattern towards a solution.

The previous image shows that we can only trap water if there is a valley-like pattern in the elevation map, meaning a low area between higher areas. So we want to find a segment where the shape is as follows: the height of the bars have a decrease, followed by an increase in height, to "catch" the rain.

Let's also look at a few maps which don't trap any water.

Solving the Problem

We can come up with several methods of computing the amount of rainwater trapped by an elevation map. We should always start by brute forcing it, and ask ourselves how we'd manually determine the result we want.

Let's take a super simple example, [5, 3, 5]. Picture it below:

1X R X
2X R X
3X X X
4X X X
5X X X
65 3 5
7
80 1 2   <-- index

Well, starting at the first element 5, we know that no rain can be trapped. So we move on. At the second element, 3, things get interesting: we know based on our observation of the element before it, it can carry up to 2 extra units of rain. Because the element that follows is also a 5, it makes sense that that shape can hold 2.

But suppose one of the surrounding hills was 6 instead:

1    X
2X R X
3X R X
4X X X
5X X X
6X X X
75 3 6
8
90 1 2   <-- index

Any rain that would reach 5 units worth can be pictured as "sliding off" the elements at index 0 and 1. So at every element, we actually want to find the two highest peaks surrounding said element, and take the second highest.

So that's the brute force solution. Here, let's see this visually: we'll discuss one simple but efficient way to calculate the result.

All we need is to determine what the maximum water level can be at each column of the whole map. To get this, read and understand the below statement very carefully, and think about it:

The maximum level of water at index i is the minimum value of the maximum heights in both directions from i. water_level(i) = min(max_height[0:i-1], max_height[i+1:n])

After determining the maximum level of water, we can just subtract the height at i from the maximum level of water to get the water height at i.

Now we need to solve how to get the maximum water levels. Believe it or not, it's already been solved by the quote I gave you earlier. Do you see it?

Here it is: we need to get the maximum height from both sides of i (left and right) to get the maximum water level at i. What if we can divide the problem into two similar problems with different directions? We can do this with two new arrays. See the image below:

First, we go from left to right and keep the maximum height found until now in a new array. Think of it as a running max height from the left.

xxxxxxxxxx

def totalRain(heights):

    if heights == None or len(heights) <= 2:

        return 0

    N = len(heights)

    max = 0

    left = [0] * N

    right = [0] * N

​

    # scan from left to right

    max = heights[0]

    left[0] = max

    for i in range(N):

        if heights[i] > max:

            max = heights[i]

        left[i] = max

    return left

​

# uncomment a different array to see the working on a different array

# arr = [0, 0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1, 0, 0] # should be 6

# arr = [0, 0, 1, 0, 2, 4, 4, 4, 2, 3, 1, 0, 2, 4, 3, 1, 0, 1] # should be 14

# arr = [0, 0, 1, 2, 4, 4, 4, 3, 1, 0, 0, 0] # should be 0

arr = [ 5, 1, 2, 4, 4, 4, 3, 1, 0, 0, 0 ] # should be 5

​

print(totalRain(arr));

Do the same for right to left

We can do the exact same thing from right to left. This will be accumulated in a new array named right[].

So finally, we get the two arrays left[] and right[] that we can use to get the maximum water level at each column. See the code to understand how we got these two.

xxxxxxxxxx

def totalRain(heights):

    if heights == None or len(heights) <= 2:

        return 0

    N = len(heights)

    max = 0

    left = [0] * N

    right = [0] * N

​

    # scan from left to right

    max = heights[0]

    left[0] = max

    for i in range(N):

        if heights[i] > max:

            max = heights[i]

        left[i] = max

​

    # scan from right to left

    max = heights[N - 1];

    right[N - 1] = max

    for i in range(N-2, 0, -1):

        if heights[i] > max:

            max = heights[i]

​

        right[i] = max

    return right

​

print(totalRain(arr))

Maximum Water Level at columni

As explained previously in the quote, now we can get the maximum water level at index/column i pretty easily. Before that, think about the values we currently have at hand on left[] and right[] arrays.

1left[i] = Maximum value of heights if we keep going to left from i.
2right[i] = Maximum value of heights if we keep going to right from i.

So what we need to do is get the minimum of these two to get the maximum water level at i. Remember, this is not yet what we want at each column/index. We want to have the amount of water at each column. So we subtract the height at i from the maximum level of water. That would be our desired value at each index.

1max_level_of_water[i] = min(left[i], right[i])
2water[i] = max_level_of_water[i] - height[i]

Finally, we can sum up the whole max_level_of_water array to get the final result. But do we really need another array max_level_of_water for this?

No, we don't! We can get the sum directly by calculating from left[] and right[] at each column and adding them (starting from 0) during the iteration. The modified pseudo code is below:

1result = sum(min(left[i], right[i]) - height[i] for i in range(n))

To understand this, I am giving you the below diagram showing the values of an example at each step and arrays.

So the final solution is given below:

xxxxxxxxxx

print(totalRain(myArr))

def totalRain(heights):

  if not heights or len(heights) <= 2:

    return 0

  N = len(heights)

  max_h = 0

  left = [0] * N

  right = [0] * N

  max_h = heights[0]

  left[0] = max_h

​

  for i in range(1, N):

    if heights[i] > max_h:

      max_h = heights[i]

    left[i] = max_h

​

  max_h = heights[N - 1]

  right[N - 1] = max_h

  for i in range(N - 2, -1, -1):

    if heights[i] > max_h:

      max_h = heights[i]

    right[i] = max_h

​

  result = 0

  for i in range(N):

    result += min(left[i], right[i]) - heights[i]

  return result

​

myArr = [5, 1, 2, 4, 4, 4, 3, 1, 0, 0, 0]

Code for Trapping Rain Water

This code is intentionally made very precise and concise by following Functional Programming principles. We do the following step by step to get the result:

1. First we check the corner/simplest cases and return 0 if found.
2. So our final result will be a sum of something.
3. sum of what? sum of minimum of two values calculated from heights. We also need to subtract heights[i] from them.
4. min of which two values? Values calculated from left-to-right at each index and right-to-left at each index.
5. So we can return all these with that one statement.

xxxxxxxxxx

def totalRain(heights):

    if not heights or len(heights) <= 2:

        return 0

    return sum(

        [min(

            max(heights[:i+1] or heights[:1]),

            max(heights[i:] or heights[-1:])

            ) - heights[i] for i in range(len(heights))

        ]

    )

​

​

if __name__ == '__main__':

        # uncomment a different array to see the working on a different array

        # myArr = [0, 0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1, 0, 0] # should be 6

        # myArr = [0, 0, 1, 0, 2, 4, 4, 4, 2, 3, 1, 0, 2, 4, 3, 1, 0, 1] # should be 14

        # myArr = [0, 0, 1, 2, 4, 4, 4, 3, 1, 0, 0, 0] # should be 0

        myArr = [5, 1, 2, 4, 4, 4, 3, 1, 0, 0, 0] # should be 5

​

        print(totalRain(myArr))