Decimal and binary

How do we usually represent numbers? We use decimal notation (a.k.a. Base 10) that provides ten unique digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. To form numbers, we combine these digits in a certain sequence so that each decimal digit represents a value multiplied by a certain power of 10.

For example, in decimal, 152 = 100 + 50 + 2 = 1×10² + 5×10¹ + 2×10⁰.

Decimal numbers are what humans like most. What computers like most are binary numbers (a.k.a. Base 2) where there are only 2 available digits: 0 and 1. As such, a binary number is a sequence of ones and zeros, e.g. 011101001, 1100110, or 110. In a binary number, each digit is referred to as bit, and each bit represents a power of decimal 2.

For humans, reading (and making sense of) binary numbers involves converting them to decimal form. Let's convert the binary number 110 to decimal notation. We know that the three digits in the number represent powers of decimal 2. In order to move from lower to higher powers of 2, we will read binary digits in our number right to left:

(Base 2) 110 = (Base 10) 0×2⁰ + 1×2¹ + 1×2² = 0 + 2 + 4 = 6

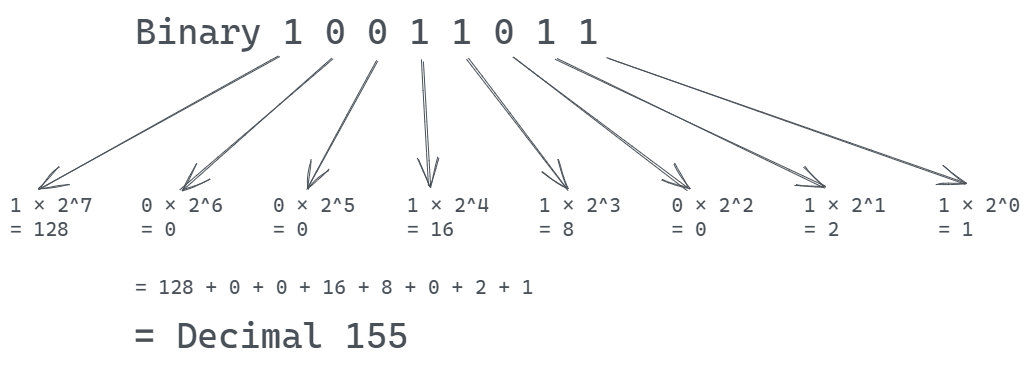
Let's try to convert a larger binary number: 10011000. Remember, we're reading binary digits right to left.

(Base 2) 10011011 = (Base 10) 1×2⁰ + 1×2¹ + 0×2² + 1×2³ + 1×2⁴ + 0×2⁵ + 0×2⁶ + 1×2⁷ = 1 + 2 + 0 + 8 + 16 + 0 + 0 + 128 = 155.