Introduction

You may have heard of a concept of state machines or more formally finite state machines. But what are they?

State machines serve as a mechanism to transition something from one state to the other. They have three key components:

• States are the possible configurations something can be in. The current state can influence what is currently happening, what values certain variables may have, and what other states are accessible from it.
• Transitions are connections between states. They allow the program to move from one state to another connected state under certain conditions.
• Events are aforementioned "certain conditions" - they are changes in a program or data it's accessing that trigger a transition from one state to the next.

All this might be a bit abstract, so let's use an everyday example to illustrate how state machines may be used to program a home appliance, like the AC. Let's assume it's set to automatic temperature adjustment.

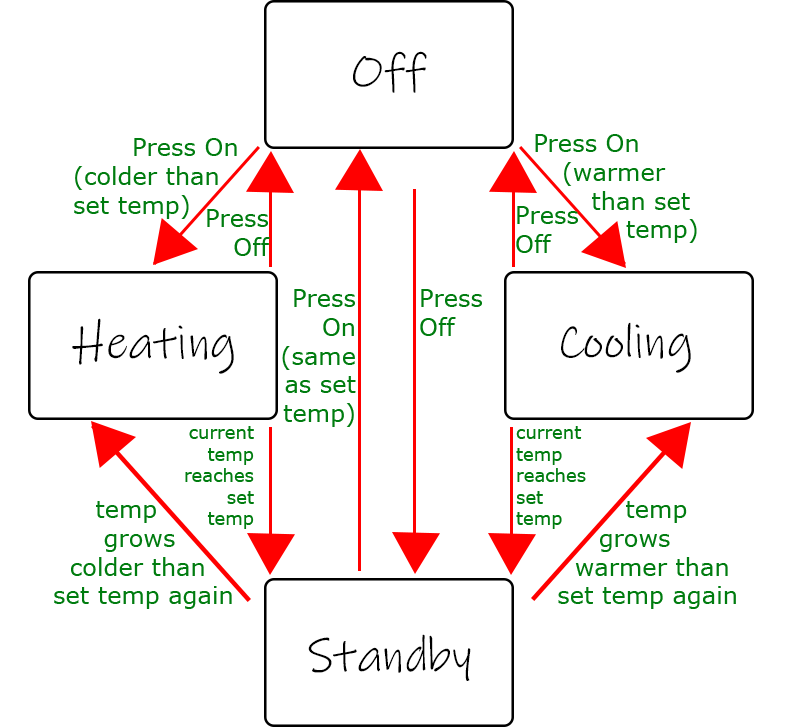
We can see in this picture the white squares are the possible states of our AC (Off, Heating, Cooling, or Standby). The states are pretty self-explanatory, with the difference between Off and Standby being that in Standby the AC is on and monitoring current temperature to see if it should start heating or cooling.

We have our red arrows that are the possible transitions and green letters for events that trigger each transition. When the AC is Off it can transition to any of the other states depending on how the current room temperature as read by the thermometer compares to the temperature we've set on the AC. If it's colder, it's going to start Heating, if it's hotter, it's going to start Cooling, and if the temperatures are exactly the same it will go into Standby. We can also return to Off state from any of the states when the Off switch is pressed. If you follow this logic, you'll see how the AC keeps the room temperature around the set value consistently.

Events and transitions are fundamentally linked, but it's important to separate them out. One event can trigger multiple transitions (such as Press Off in our example) depending on the state we're currently in or trigger different transitions (such as Press On) depending on values of current variables. In a larger system, an event can be a complex trigger, setting off many procedures and transitions, and the state machine would be just one of its subscribers, waiting for their signal to determine what to do.

Transducers - Meley and Moore

Transducers are state machines that produce output. In a sense, their purpose is to produce output, otherwise, they're useless. In the case of state machines, the output isn't text on a screen or a return variable, but instead the effect of state changes.

There are two types of state machines depending on how they deal with output - Meley and Moore.

Moore state machine produces output when it enters a certain state or the whole time it is in that state. Think of the AC example from before. When we're in Heating state and we press the off button, the machine changes its state to Off, and entering that state produces the output of sending a signal to turn off the AC. When we press On, entering one of the states will cause the machine to continuously perform a certain task (heat, cool off, check the current temperature, and compare it to goal) so long as it's in that state.

Meley state machines are different. They don't produce output while in a state. Their output happens during the transition. Often this is achieved through changing values of certain variables in certain cases. Let's look at how our AC state machine could look in this case:

As we can see, we can have cycles that don't switch us to an entirely new state but instead just control some variables relevant to how we execute the current state. These two things are equivalent, but sometimes it will be more intuitive or easy to represent or implement things one way or the other.

It's important to note that output effects during a transition will often be implemented as effects that happen when entering a state. This implementation has the same effect as the change happening during the transition, though this may be confusing. But as we'll see, the concepts of Meley and Moore machines are often blurred in practice anyway.

Often, you'll find both Meley and Moore state machines mixed within the same diagram or implementation. Sometimes one or the other will be more convenient for expressing an idea. That's why when implementing state machines, it's advisable to allow for actions on entering a state, while in a state, or while exiting a state.

Transductors - Harel State Charts

Harel state charts expand this even further by allowing more levels of abstraction. They combine Meley and Moore state machines and add additional concepts:

• Hierarchy allows us to be in multiple states of our state machine at once. For instance, we could add another state to our AC diagram - On.

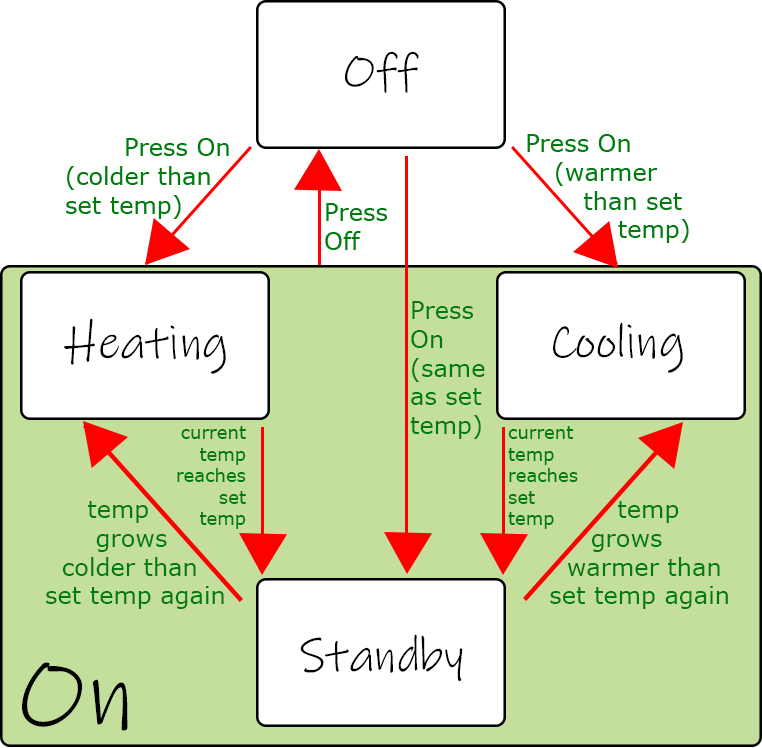
• Parallelism allows two or more separate state machines to work in parallel, yet be displayed on the same diagram. We'd use this if their effects are tied in a way that makes it easier to understand them together.
• Broadcasting allows state machines to communicate with each other by broadcasting certain signals that the other state machine may pick up on. For instance, our AC could have two separate state machines for its fans and its thermostat. But the thermostat should broadcast the change in temperature to the fans so they could decide when to go into standby and when to work.

Acceptors

State machines that change states depending on some input and then produce a binary output are called acceptors. That name is derived from the fact that they're often used to either accept or reject some input, such as a sequence of characters or a sequence of tokens. They're often used to implement frontends of compilers.

Let's start with a simple example. This acceptor checks whether a binary number has an even number of 0s or not. The circle within a circle state indicates a state in which we can end with an even number of zeros. If the input ends in any other state, that means the number is odd (or in the general case, the state machine outputs false). We can have multiple of these end states, but in our even-odd example, there's going to be only one.

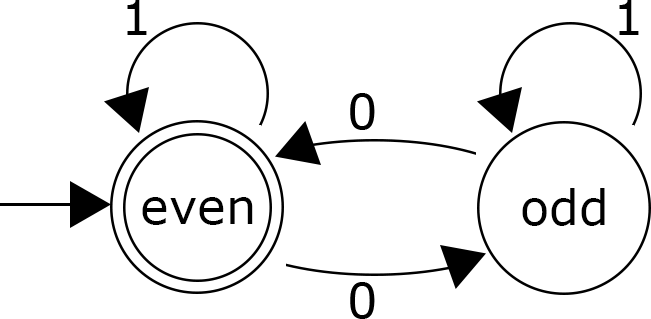
The arrow entering even from nowhere is the starting point of the state machine. It can have only one starting point from which it can go into various states depending on the input. A set of possible inputs of a state machine is its alphabet. In the case of our even-odd example, the alphabet would be [0,1]. If any other character is received, it would go into an error state. Sometimes that error state is explicitly drawn, but if it's not on the diagram it just means "any input other than these causes error".

Let's say we want to detect whether a username belongs to our company employee or not, and assume our mandated format is name.sur, where name is persons full first name, while sur is the first three letters of a surname. We could do something like this:

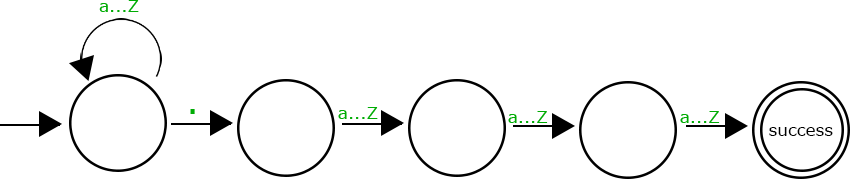
This state machine will take any number of letters (indicated by a cyclical transition), then a point, and then exactly three letters for the surname. In our case, this is case insensitive. Think about how you could make a case-sensitive version of this.

Two major algorithms allow us to turn any regular expression into a finite state machine, called Thompson's construction and Glushkov's algorithm. We won't get into them in this article, but if you want to study this subject more deeply, they're a must.

Acceptors with a single-letter input alphabet are called sequencers.

There's also a class of state machines similar to acceptors, but which can produce n-ary output instead of binary. This means that instead of just differentiating between true or false, even or odd, etc. it can classify given input into n different classes. These state machines are, accordingly, called classifiers.

Determinism

Deterministic finite state machine (DFSM) is a state machine that always gives the same output for the same input. This means:

• no two transitions from the same state happen under exactly the same conditions; and
• no transitions happen without empty input (so-called epsilon input).

DFSM are also known as deterministic finite automata or deterministic finite acceptors (both abbreviated as DFA).

All other state machines are non-deterministic (NDFSM).

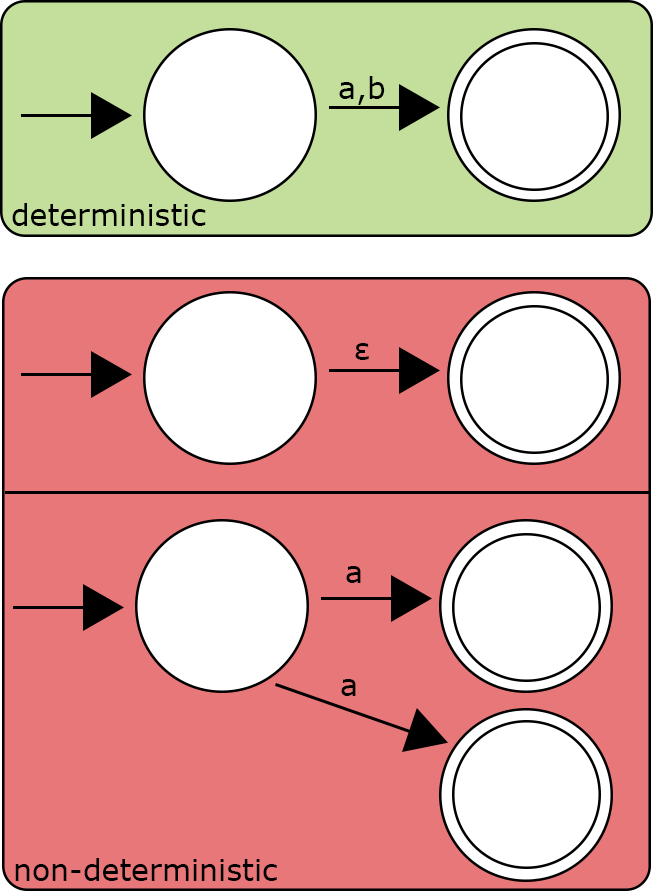
There are algorithms to convert an NDFSM to a DFSM, but they're also beyond the scope of this article.

Applications of State Machines

There are many applications of state machines in computer science and wider. They're primarily used for systems that change their states instantaneously between certain discreet values. Systems that change gradually, continually, are not suited for representation and programming through state machines.

Applications of state machines include language definition and analysis, game development, engineering, programming electronics with discreet inputs, evolutionary simulations, UI programming, and many more.

Think about how you could apply this to detect valid input for a compiler front-end. Or, if that interests you more, how you could use it to switch between states such as Idle, Walk, Run, Jump, etc. in a video game and swap animations along the way. Maybe you want certain parts of UI to appear differently depending on the state your user is in, so they'd maybe be less obtrusive during certain high-focus tasks or maybe some parts of your UI are mutually exclusive to avoid screen clutter - those could benefit from being implemented through a state machine. Whatever your field of interest, take some time to think about how you could apply this and tinker with it. That's the best way to learn.

One Pager Cheat Sheet

• State machines, composed of States, Transitions, and Events, are mechanisms used to program a machine's response to a set of conditions and transition it from one state to another, illustrated in the example of an AC.
• Yes, a state machine can be used to program everyday appliances, by defining states, transitions, and events.
• A state machine is a logical system based on states, inputs, and transitions that can be used to program everyday appliances without requiring any actual data or signal transmission.
• The output of Meley and Moore state machines differs based on when they produce output - Meley when transitioning between states and Moore when entering and remaining in states.
• Meley state machines produce output during a transition between states, whereas Moore state machines produce output when entering or remaining in a state.
• Harel state charts enable hierarchy, parallelism, and broadcasting to be represented on the same diagram, allowing for more levels of abstraction than Meley and Moore state machines.
• Acceptors are state machines that accept or reject some form of input, like a sequence of characters or tokens, by changing states and producing either a binaries output (such as even/odd) or n-ary output (e.g. classify the input into distinct classes).
• A fail state is always present in state machines, even if it is not explicitly labeled, and can be entered if an invalid character is received.
• The Acceptor will verify and confirm that an email is from a trusted domain, allowing it to pass if it is genuine or alerting the user if not.
• A Deterministic finite state machine (DFSM) is a state machine that always gives the same output for the same input, while all other state machines are non-deterministic (NDFSM).
• DFSMs cannot transition between states without epsilon input, unlike NDFSMs, which can transition without any input.
• A deterministic state machine will always transition from the same set of inputs to the same state, whereas a non-deterministic state machine can transition to different states for the same set of inputs.
• If the output of a state machine is not determined by the input due to the possibility of multiple states being transitioned to, then the machine is considered non-deterministic.
• This code example demonstrates how a state machine with a hash map can be implemented, with states corresponding to circles and transitions corresponding to arrows on a diagram.
• Applications of state machines can provide various benefits, such as language definition and analysis, game development, programming electronics, and UI programming, which can be used to detect valid input or switch between states such as Idle, Walk, Run, and Jump.