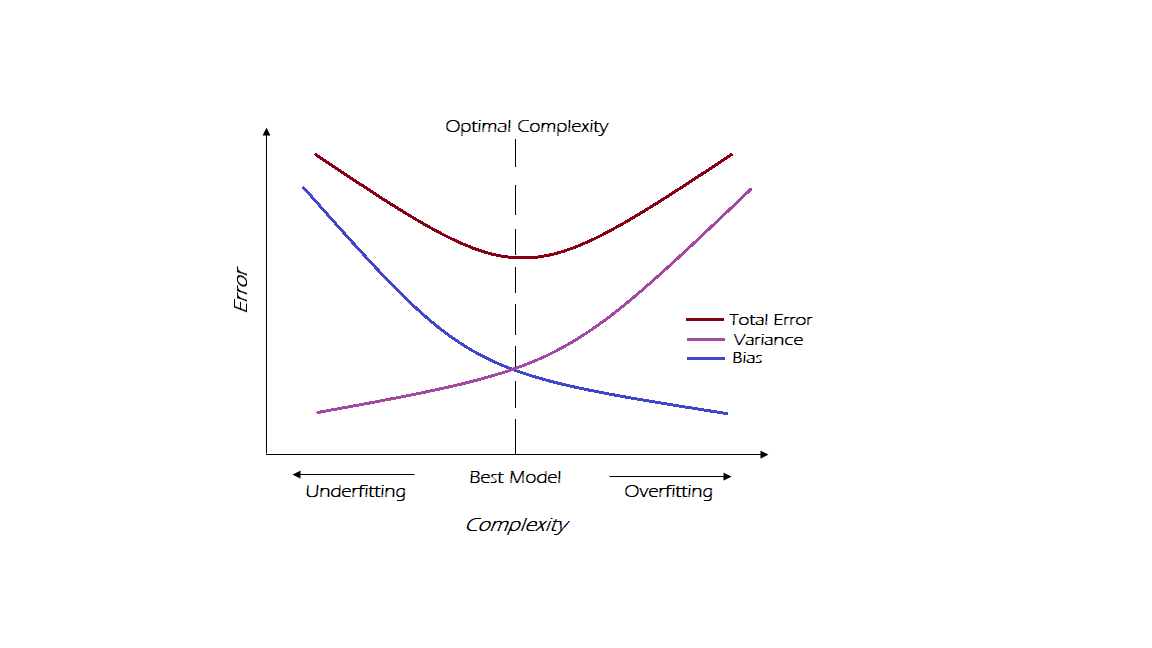
1. What is bias variance trade-off?
Bias and variance are known as prediction errors of a model. An oversimplified model leads to high bias, a measure of how far the predicted values of the model are from the correct values.
A more complex model can lead to high variance, meaning more variation in the predictions between model iterations. However, these two errors are inversely proportional to each other.
The goal of any supervised machine learning algorithm is to have low bias and low variance to achieve strong prediction performance. Therefore, a balance is maintained between these two and this is called the bias-variance trade-off.
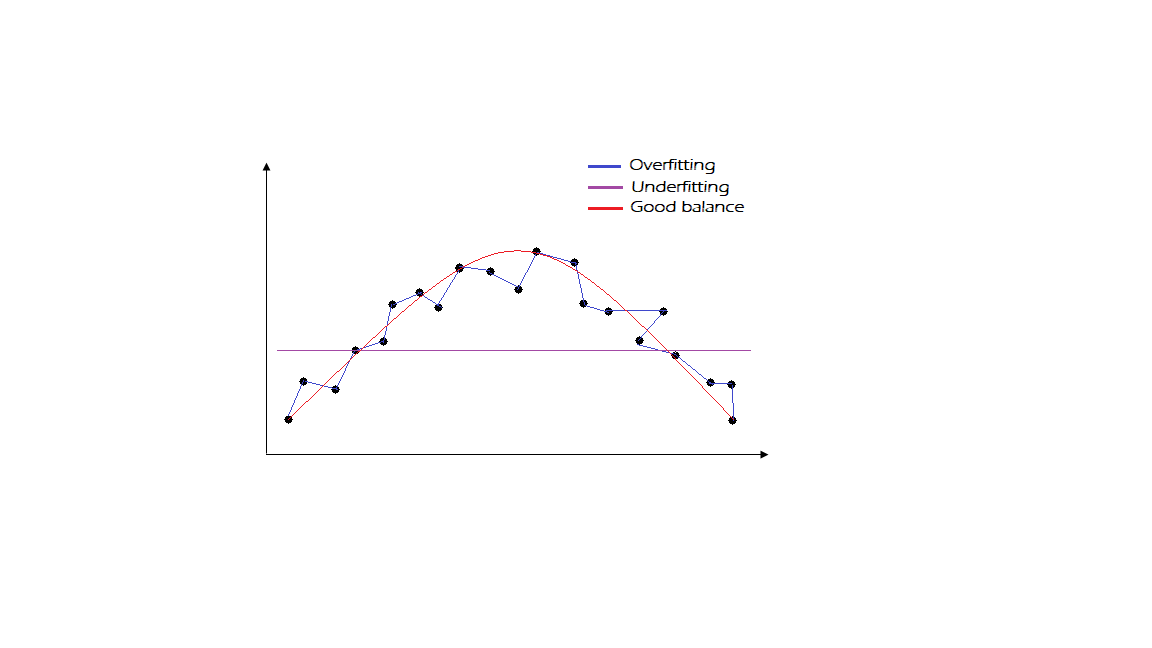
2. How do we combat Over-fitting and Under-fitting?
To combat overfitting and underfitting, you can resample the data to estimate the model accuracy (k-fold cross-validation) and by having a validation dataset to evaluate the model.
3. How would you effectively represent data with multiple dimensions?
We can use a method like a pair-wise correlation matrix or pair-wise scatter plot. Another common solution is to change the data and use traditional 2D and 3D data visualization techniques. There are 3 options to adjust the data:
- Feature selection
- Feature extraction
- Manifold learning
4. How is k-NN different from k-means clustering?
| K-NN | K-Means |
|---|---|
| Unsupervised learning algorithm | Supervised learning algorithm |
| Use for Clustering | Use for Classification |
| It takes a bunch of unlabeled points and tries to group them into “k” number of clusters. | It takes a bunch of labeled points and uses them to learn how to label other points. |
5. How would you validate a model you created to generate a predictive model of a quantitative outcome variable using multiple regression?
To model a qualitative dependent variable such as a simple yes/no,
we can use logistic regression.
The first step is to split the data in the ratio of 70-30 or 60-40. We can keep large data for building/training the model and use the rest to validate the trained model.
The final step is to review the residuals of your model on both sets of data and look at other parameters such as R squared and standard error.



