AlgoDaily - Problem Solving With Recursion vs. Iteration

Home > Data Structures and Algorithms 🚀 > Understanding Recursion > Problem Solving With Recursion vs. Iteration

Iteration and recursion are both techniques that you can use for implementing solutions in a programming language. I look at both of them as a way of thinking about a problem and solving it. The most important thing to keep in mind before we start discussing them is:

For any problem that can be solved via iteration, there is a corresponding recursive solution and vice versa.

For a programmer, it is important to understand both techniques, and be aware of their differences and when to resort to one technique in favor of the other. Let's start!

Iteration

Iteration is simply the repetition of a block of code in a program. In many cases, we need a control variable to implement iteration. Alternatively, we can repeatedly execute a block of code until a certain stopping criterion is met.

Generally you can implement iteration using for, while or do-while loop constructs (in some programming languages we have the alternate repeat construct). Let's look at an example pseudo-code, where we print numbers from 1 to 5 using a control variable i.

As the values of i change in the loop, the numbers 1, 2, 3, 4, 5 are printed. The loop is executed as long as the condition i <= 5 holds true.

xxxxxxxxxx
 
let i = 1; // Initial value of control variable
// Repeat the next block till condition i <= 5 is true
while (i <= 5) {
  console.log(i); // Print i
  i = i + 1; // Increment i by 1
}

Recursion

Recursion is a technique based on the divide and conquer principle. That principle calls for us to define the solution of a bigger problem in terms of the solution of a smaller version of itself.

In a programming language, a recursive function is one that calls itself. Let's look at the pseudo-code of a recursive function that prints the numbers from 1 to 5. You can invoke the function printList like printList(1).

The code is pretty cool as it will, like our iterative counterpart, also print the numbers 1, 2, 3, 4, 5. printList is a recursive function as it calls itself. We'll learn how it works in a bit.

xxxxxxxxxx
 
function printList(i) {
  // Base case: If i is greater than 5, return without doing anything
  if (i > 5) {
    return; // Do nothing
  }
  // Recursive case: Print the value of i
  console.log(i);
  // Call the function with i + 1
  printList(i + 1);
}

Two Parts of a Recursive Solution

Recursion is implemented by defining two scenarios, both of these are marked in the printList function:

Base case: This is the non-recursive case (the part that doesn't trigger another call) and defines when to stop (or the smallest version of the problem).
General case / Recursive case: Defines how to solve the problem in terms of a smaller version of itself. Each general case should get you "closer" to the base case.

Try this exercise. Is this statement true or false?

In theory, if a base case is not defined for a recursive function, the code will raise an exception.

Press true if you believe the statement is correct, or false otherwise.

How Recursion Works: The Activation Stack

The pseudo-code for the printList function can only be implemented in what we call "a stack based language". These languages keep track of all the functions, which have been invoked at runtime using a data structure called the activation stack. They allow functions to call themselves, by saving their state (local variables and parameters) on a stack, and invoking them again.

Everytime a function is called, its entire state including its local variables and pass by value parameters are saved as a record on the stack. When the function exits, its corresponding record is popped off this stack.

A recursive call would therefore push a record of the function on the stack. Then, the base case would start a process called "unwinding recursion" and slowly the records would be popped off the stack.

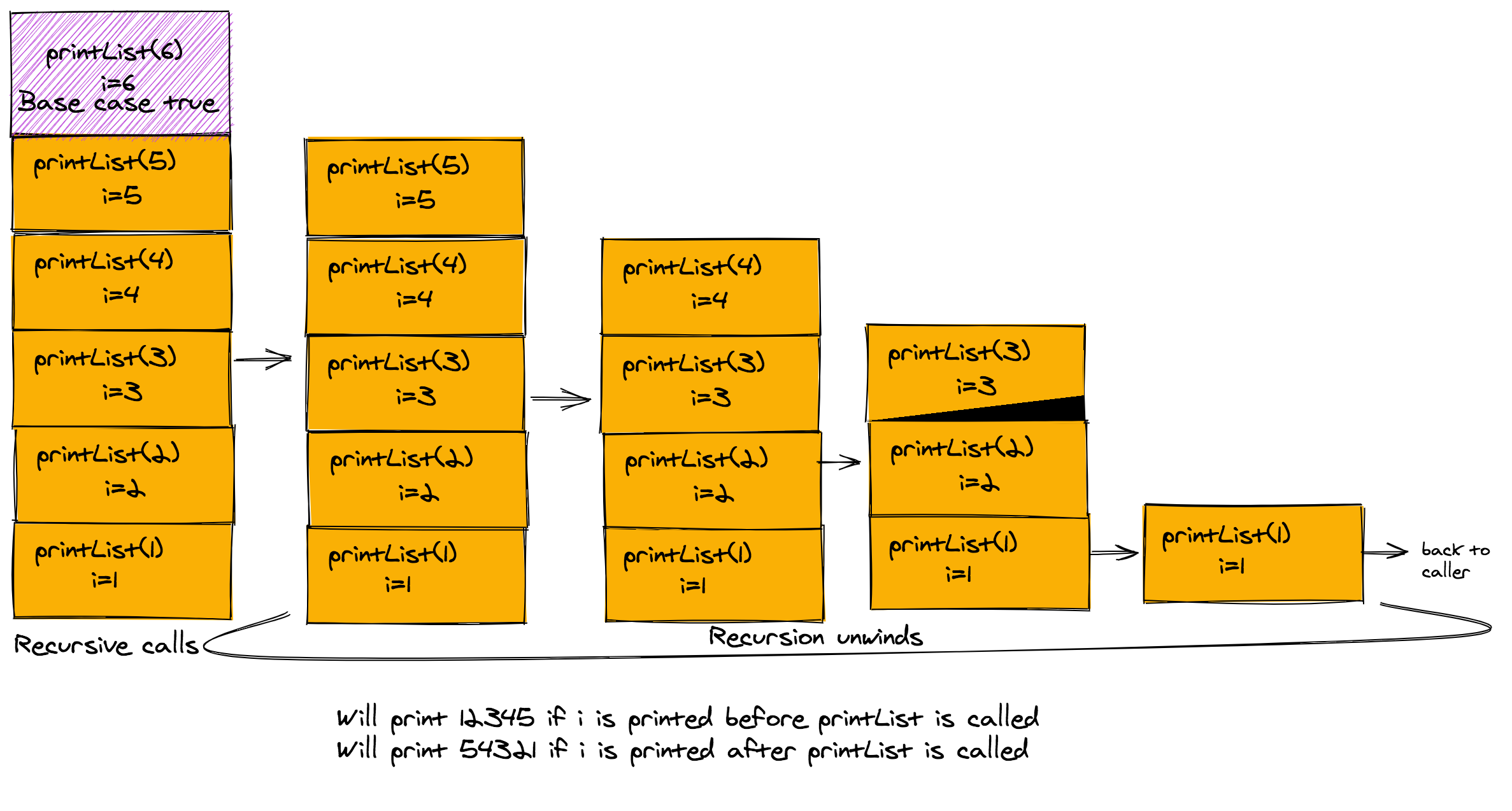
How Recursion Works The Activation Stack

The diagram above shows the activation stack for printList. Note how the system preserves various copies of the printList function, with each copy having its own value of the variable i. The stack is built until the condition for the base case holds true. After that the records from the stack are popped off.

Reversed

What happens if you reverse the statements in printList?

Well, now the function is being called before printing the value of i. So the values are printed during the "unwind recursion" phase, after the base case is invoked. This would print the values in reverse (in other words, 5, 4, 3, 2, 1).

xxxxxxxxxx
 
function printList(i) {
  // base case
  if (i > 5) {
    return; // do nothing
  }
  // recursive case
  printList(i + 1);
  console.log(i);
}
​
printList(1);

Factorial

Now that we understand both iteration and recursion, let's look at how both of them work.

As we know factorial of a number is defined as:

n! = n(n-1)(n-2)...1

or in other words:

n! = n(n-1)!

Let's now implement both an iterative and recursive solution for factorial in C++.

Both solutions look intuitive and easy to understand. The iterative version has a control variable i, which controls the loop so that the loop runs n times. For the iterative solution, we know in advance exactly how many times the loop would run.

The recursive version uses the second definition: n! = n * (n - 1)!, which is naturally a recursive definition. It defines the factorial of n in terms of the factorial of a smaller version (n - 1). We don't need to specify in advance, how many times the loop will run.

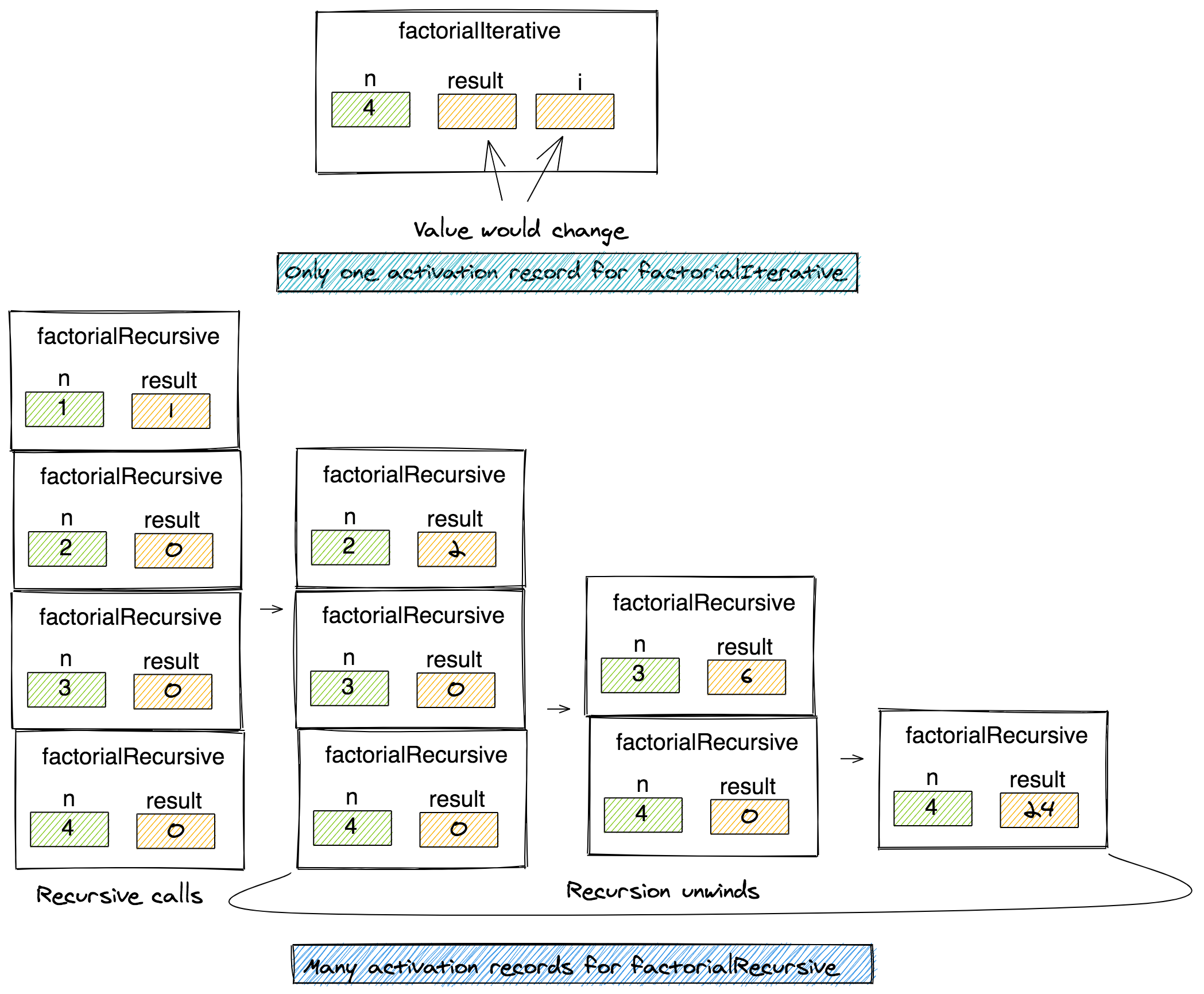
xxxxxxxxxx
 
// Iterative
function factorialIterative(n) {
  let result = 1;
  for (let i = n; i >= 1; i--) {
    result = result * i;
  }
  return result;
}
​
// Recursive
function factorialRecursive(n) {
  let result = 0;
​
  if (n == 1)
    // base case: n==1
    result = 1;
  // recursive case
  else result = n * factorialRecursive(n - 1);
​
  return result;
}
​
factorialIterative(4);
factorialRecursive(4);

Working of Factorial: Iterative vs. Recursive Case

Look at the diagrams below to see the "behind the scenes" portion of the activation stack for both the iterative and recursive cases:

The most important thing to note is that the iterative version has only one function record on the activation stack. For the recursive cases, there are 4 records of the function on the activation stack until the recursion starts to unwind.

So imagine what would happen if you were to call factorial for a larger number like 10 or 20. So many records on the activation stack is a strain on the system's memory! There is also the extra overhead of function calling, saving its state, and maintaining the activation stack.

If you are using a programming language like C++ or Java, then go for the iterative solution as it would run in constant memory.

Try this exercise. Click the correct answer from the options.

Which of the following statements are correct?

Click the option that best answers the question.

Recursion should be used when the problem is repetitive
Iteration cannot be used on every recursive problem
Iteration uses activation stack
Recursion uses less memory as compared to iteration

Quick Sort: Think Recursively!

From the factorial example, we learned not to use recursion. So why is every computer scientist in such awe with regards to this technique?

Well, the answer is that if you look at some problems, you'll find that they are naturally recursive in nature. The solution to such problems is conceptually easier to implement via recursion, and harder to implement via iteration. Let's analyze the pseudo-code for quick sort first, and then we'll see its various solutions. Note: I am using pivot as the middle item of the array.

See how the solution says that we will "apply the sort to a smaller version of the array" to sort the entire array. The following diagram also called the recursion tree shows the working of quickSort.

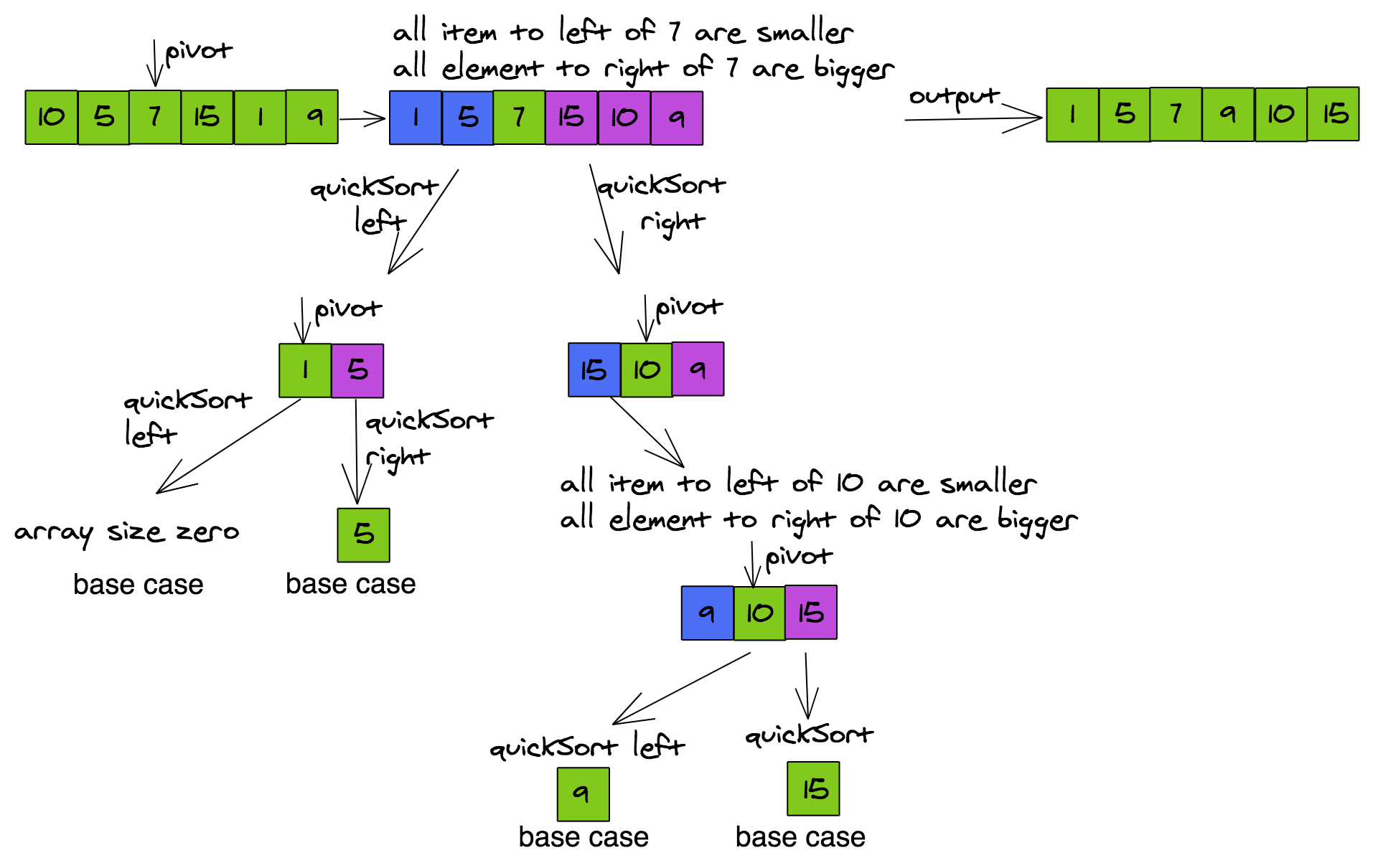
xxxxxxxxxx
 
quickSort
input: array
output: sorted array
​
Base case:
1. If the array size<=1 then the array is sorted
Recursive case:
1. Find the pivot of the array
2. Adjust all items less than pivot on the left side of pivot
3. Adjust all items greater than pivot on the right side of pivot
4. quickSort the subarray to the left of pivot
5. quickSort the subarray to the right of pivot

Quick Sort Implementation

The recursive version of quick sort is very easy to implement, and is shown in the right box. See how elegant and easy it is?

Most people looking at the code can meaningfully understand the "concept" behind quick sort. It first adjusts items around the pivot, and then calls quickSort recursively on both left and right subarrays.

xxxxxxxxxx
console.log(vect);
 
function exchange(a, i, j) {
  let temp = a[i];
  a[i] = a[j];
  a[j] = temp;
}
​
function adjust(A, start, end, pivot) {
  let a = start, b = end;
  let stop = false;
  while (!stop) {
    while (a < pivot && A[a] <= A[pivot])
      a++;
    while (b > pivot && A[b] >= A[pivot])
      b--;
    if (a >= pivot && b <= pivot)
      stop = true;
    else {
      exchange(A, a, b);
      if (a === pivot)
        pivot = b;
      else if (b === pivot)
        pivot = a;
    }
  }
}
​
function quickSortRecursive(A, start, end) {
  if (end - start < 0)
    return;

But What About Iterative?

Now let's think of the iterative version. It's not as straightforward to implement!

We can apply the pivot and adjustment of items around the pivot, only on one subarray at a time. If we work with the left subarray, then we need to store the indices of the right subarray to be used later for repeating the process. This necessitates the implementation of our own stack that will maintain the indices of left and right subarrays to work with, instead of using the implicitly built system activation stack for recursive functions.

In the code here for the iterative version of quickSort, we have two stacks of the same size. One holds the start index of the subarray and the other holds the end index of the subarray. Once values are adjusted around the pivot for one subarray, the other subarray's start and end indices are popped from the stack.

xxxxxxxxxx
console.log(vect);
 
function exchange(a, i, j) {
  let temp = a[i];
  a[i] = a[j];
  a[j] = temp;
}
​
function adjust(A, start, end, pivot) {
  let a = start, b = end;
  let stop = false;
  while (!stop) {
    while (a < pivot && A[a] <= A[pivot])
      a++;
    while (b > pivot && A[b] >= A[pivot])
      b--;
    if (a >= pivot && b <= pivot)
      stop = true;
    else {
      exchange(A, a, b);
      if (a === pivot)
        pivot = b;
      else if (b === pivot)
        pivot = a;
    }
  }
}
​
function quickSortIterative(A, start, end) {
  let startIndex = [];
  let endIndex = [];

Iteration or Recursion for Quick Sort?

Of course, the main question now is: which solution to go for, iterative or recursive?

I would still advise you to go for the iterative solution. Imagine sorting an array with a million items. The system stack would need to save a significant number of records of the quick sort function. It opens you up to problems, like running out of memory, resulting in segmentation faults, etc.

Having said that, the recursive version is so much easier to write and understand. So I would go for implementing a recursive version first (and for interviews), and then thinking about how to implement it iteratively using your own stack (optimize later).

Towers of Hanoi

The last problem that I would like to talk about in this tutorial is the Towers of Hanoi game, which again is an example of a wonderful naturally recursive problem.

The Problem

You have 3 shelves (A, B, C) and N disks. Each disk is a different size and stacked such that a smaller disk is placed on top of a larger disk.

You are not allowed to place a bigger disk on top of a smaller disk. The target of the game is to move all disks from one shelf to another, using the third one as an intermediate storage location.

At any point you are not allowed to violate the rule of the game. Thus, a smaller disk is always on top of a bigger disk.

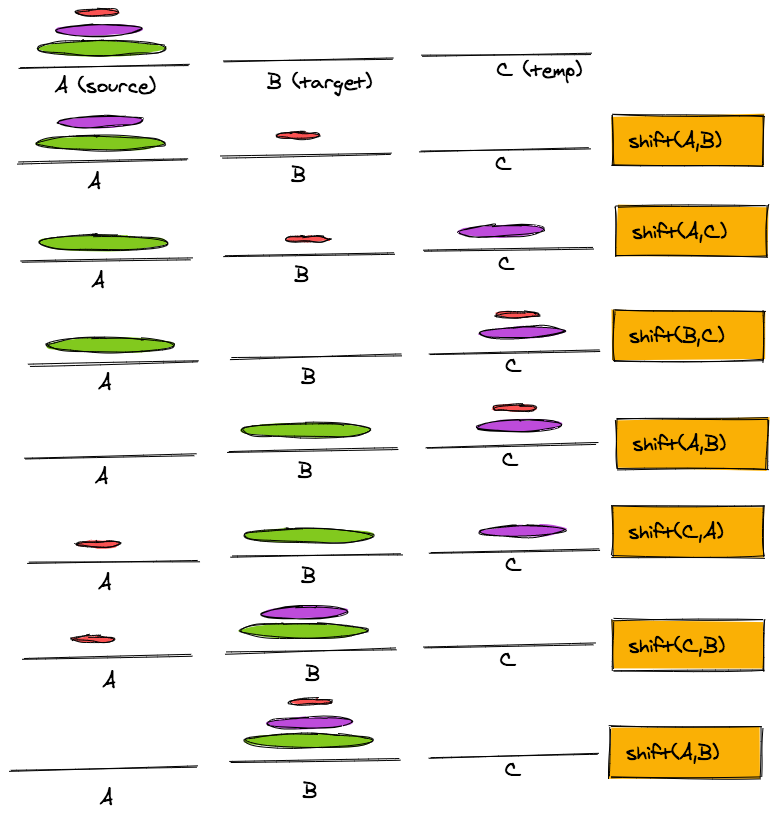
Below is an example of 3 disks of different sizes. I have made them all in a different color. The starting and goal configurations are shown in this figure.

An Awesome Recursive Solution

The best way to figure out a solution is to think logically and recursively. Break down the problem into a smaller version of itself.

If we can somehow figure out how to move N-1 disks from source shelf to intermediate shelf, using the destination as an intermediate location, then we can move the biggest disk from source to destination. Next, we can move the N-1 disks from intermediate shelf to the target, using source shelf as intermediate location. The diagram below will help in visualizing this.

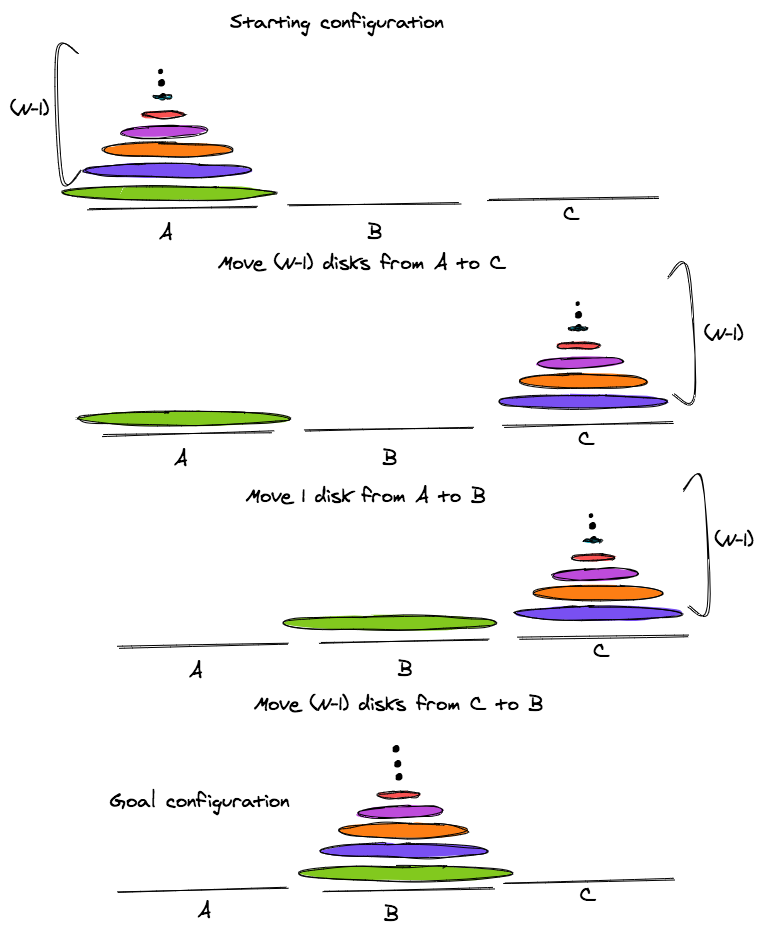
The pseudo-code is therefore very simple.

xxxxxxxxxx
 
Recurisve routine: Hanoi
Input: source shelf, target shelf, intermediate shelf, N disks placed on source shelf
Target: N disks placed on target shelf
​
Base case:
1. If there are zero disks then stop.
Recursive case:
1. Move (N-1) disks from source to intermediate using destination as intermediate shelf
2. Shift the last disk from source to destination
3. Move (N-1) disks from intermediate to destination using source as intermediate shelf

Recursion Tree for Hanoi

Figure below shows the recursion tree for a 3 disk problem

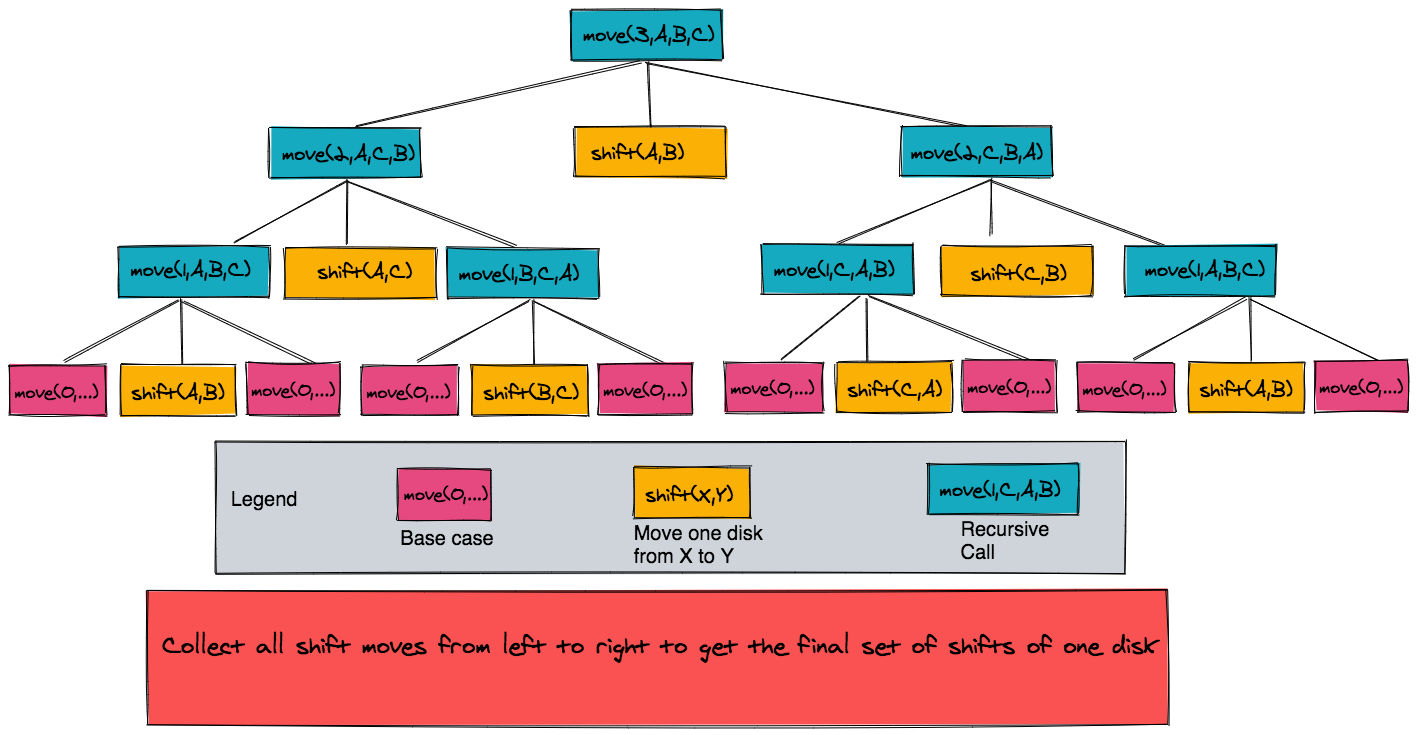
Collect together all the shift moves to have the final solution:

Attached is the beautiful recursive code for Towers of Hanoi done in C++ using the pseudo-code given previously. As you can see, it is a direct translation of the pseudo-code we wrote beforehand.

xxxxxxxxxx
 
function shift(shelf1, shelf2) {
  console.log("Shift from " + shelf1 + " to " + shelf2);
}
​
function Hanoi(N, source, destination, intermediate) {
  // base case
  if (N === 0)
    return;
  // recursive case
  Hanoi(N - 1, source, intermediate, destination);
  shift(source, destination);
  Hanoi(N - 1, intermediate, destination, source);
}
​
// example call for the illustrated problem
Hanoi(3, 'A', 'B', 'C');

Iterative Code for Towers of Hanoi

So are you up for the challenge? Of course you are! We have to figure out an iterative solution.

The best thing we can do is define a stack for source, destination, intermediate and N. You can see that steps 1, 2, and 3 of the recursive case have to be executed in the same order.

This means we first push whatever corresponds to step 3 (to be executed last). Next, we push whatever corresponds to step 2 of the recursive case. Lastly, push whatever corresponds to step 1 of the recursive case.

This is typically how you would approach the solution of a recursive solution via iteration using a temporary stack. So here is a very elegant iterative solution for Towers of Hanoi.

xxxxxxxxxx
h.solve(3, 'A', 'B', 'C');
 
class HanoiIterative {
  constructor() {
    this.sourceStack = [];
    this.destinationStack = [];
    this.intermediateStack = [];
    this.NStack = [];
  }
​
  shift(shelf1, shelf2) {
    console.log("Shift from " + shelf1 + " to " + shelf2);
  }
​
  pushStacks(s, d, i, n) {
    this.sourceStack.push(s);
    this.destinationStack.push(d);
    this.intermediateStack.push(i);
    this.NStack.push(n);
  }
​
  popStacks() {
    this.sourceStack.pop();
    this.destinationStack.pop();
    this.intermediateStack.pop();
    this.NStack.pop();
  }
​
  solve(N, source, destination, intermediate) {
    if (N <= 0)
      return;

Let's test your knowledge. Fill in the missing part by typing it in.

How many recursive calls will be required to check if the number 37 is prime using recursion?

Write the missing line below.

Take Away Lesson

Even though problems like Towers of Hanoi are naturally recursive problems with easy implementations using recursion, I still advise you to do their final implementation in languages like Java, C++ etc. using the iterative technique.

This way only one activation record would be pushed on the stack for the iterative function. However, when given such problems, always write the recursive mathematical expression or recursive pseudo-code for them, and then figure out how to implement them iteratively.

Iterative functions would be faster and more efficient compared to their recursive counterparts because of of the lack of activation stack overhead.

Some functional programming languages like LISPhave built in techniques to handle tail recursion without building a large activation stack. They are pretty cool, in the sense that they allow you to code everything using recursion, without the extra overhead of activation stack.

I hope you enjoyed this lesson as much as I enjoyed creating it.

Let's test your knowledge. Could you figure out the right sequence for this list?

How would you replace recursion with iteration? Select the correct order.

Press the below buttons in the order in which they should occur. Click on them again to un-select.

Options:

Remove an element from the array
Initialize a loop
Initialize an empty array for storing elements
Perform the necessary calculation
Add an element to array

One Pager Cheat Sheet

Both iteration and recursion can be used to solve programming problems, but an important thing to keep in mind is that for any problem that can be solved via iteration, there is a corresponding recursive solution and vice versa.
Iteration is the repetition of a block of code using control variables or a stopping criterion, typically in the form of for, while or do-while loop constructs.
A recursive function is one that calls itself, such as the printList function which uses the divide and conquer principle to print the numbers 1 to 5.
The printList function implements recursion by defining a base case (the non-recursive part) and a general / recursive case (defining how to solve the problem in terms of a smaller version of itself).
The execution of a recursive function without a base case will not raise an exception, but can lead to stack overflow if the maximum number of recursive calls is exceeded.
Recursion is a technique that enables a function to save its local variables and parameters on an activation stack, which is then popped off when the function exits or the base case is reached.
The printList function will print the values in reverse, 5, 4, 3, 2, 1, when the statements are reversed, which happens during the "unwind recursion" phase after the base case is invoked.
We can calculate the factorial of a number using either an iterative or recursive implementation in C++.
The iterative solution is more efficient for programming languages such as C++ or Java as it runs in constant memory, compared to the recursive solutions which generates 4 records on the activation stack for each call.
The recursive version of the factorial function takes up more memory due to increased activation stack records, while being less optimal in languages like C++ and Java.
Quick Sort is a naturally recursive sorting algorithm that divides the entire array into smaller pieces, and is conceptually easier to implement via recursion.
The clear concept behind Quick Sort is easily understood from the elegant and simple recursive version of the algorithm, which adjusts elements around a pivot before calling quickSort recursively on both subarrays.
We need to implement our own stack to maintain the indices of the left and right subarrays for the iterative version of quickSort.
Of course, the main question now is: which solution to go for, iterative or recursive, and I would still advise you to go for the iterative solution to avoid segmentation faults while the recursive version is easier to write and understand.
The Towers of Hanoi game is an example of a naturally recursive problem in which you move disks from one shelf to another while following a rule that a smaller disk cannot be placed on top of a larger disk.
Break down the problem into a smaller version of itself to solve it recursively using an intermediate location when moving disks.
The figure shows the Recursion Tree for the 3 disk Towers of Hanoi problem, with the final solution being derived from a direct translation of the pseudo-code in C++.
We can solve the Towers of Hanoi problem using an iterative approach by pushing step 3, then 2 and then 1 onto a temporary stack.
The number of recursive calls required to check if the number 37 is prime using recursion is three, due to the base case and subsequent checks for divisibility.
Using an iterative technique instead of recursion can be more efficient when solving problems like Towers of Hanoi since there would be no overhead associated with the activation stack.
Replace recursion with iteration by initializing an empty array, iterating through it with a loop, removing each element for processing, making the relevant calculations, and finally, adding it back to the array.