Quick Sort: Think Recursively!

From the factorial example, we learned not to use recursion. So why is every computer scientist in such awe with regards to this technique?

Well, the answer is that if you look at some problems, you'll find that they are naturally recursive in nature. The solution to such problems is conceptually easier to implement via recursion, and harder to implement via iteration. Let's analyze the pseudo-code for quick sort first, and then we'll see its various solutions. Note: I am using pivot as the middle item of the array.

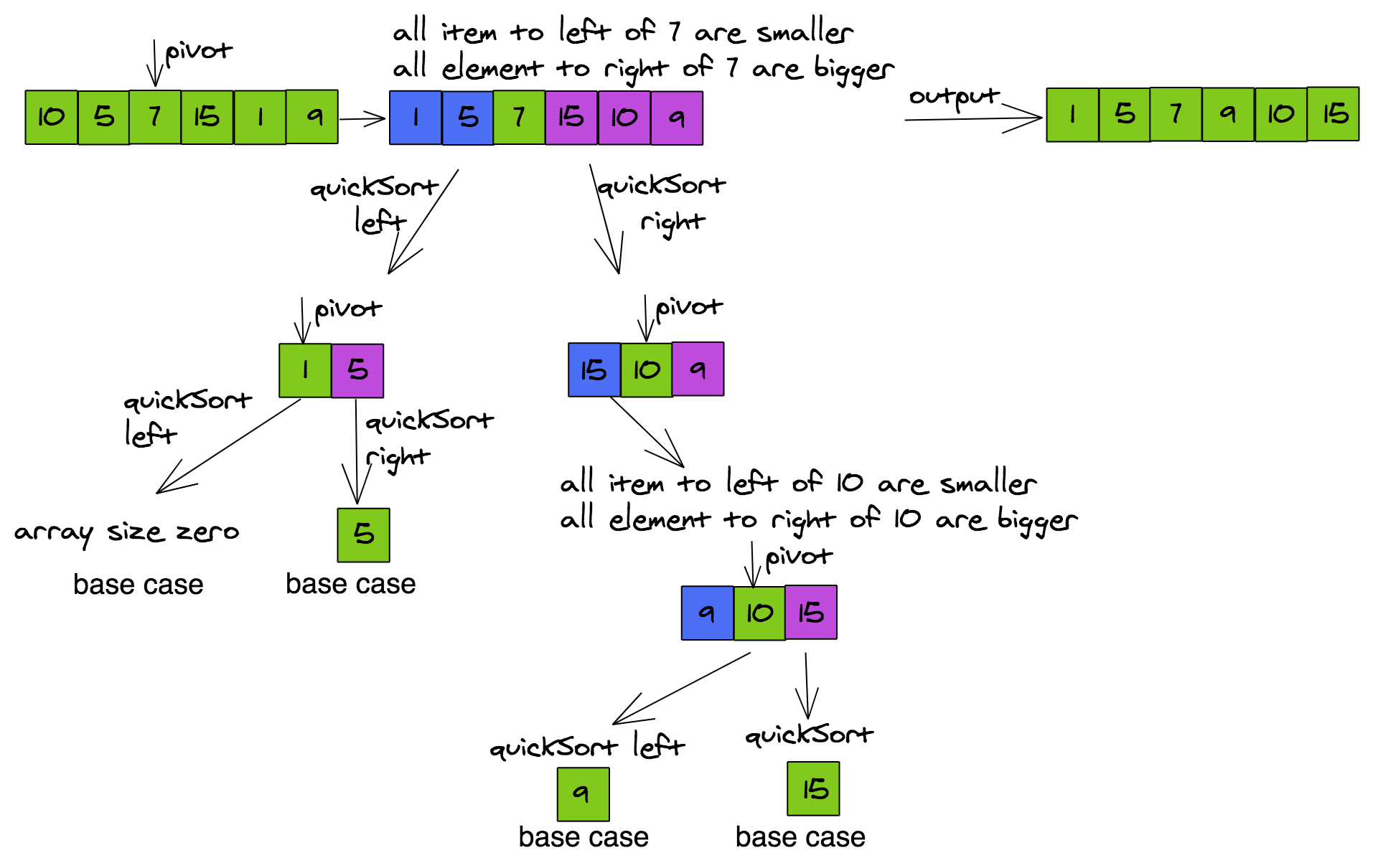
See how the solution says that we will "apply the sort to a smaller version of the array" to sort the entire array. The following diagram also called the recursion tree shows the working of quickSort.

xxxxxxxxxx

quickSort

input: array

output: sorted array

​

Base case:

1. If the array size<=1 then the array is sorted

Recursive case:

1. Find the pivot of the array

2. Adjust all items less than pivot on the left side of pivot

3. Adjust all items greater than pivot on the right side of pivot

4. quickSort the subarray to the left of pivot

5. quickSort the subarray to the right of pivot