Recursive Backtracking For Combinatorial, Path Finding, and Sudoku Solver
Backtracking Made Simple
Backtracking is a very important concept in computer science and is used in many applications. Generally, we use it when all possible solutions of a problem need to be explored. It is also often employed to identify solutions that satisfy a given criterion also called a constraint.
In this tutorial, I will discuss this technique and demonstrate it. We'll achieve understanding through a few simple examples involving enumerating all solutions or enumerating solutions that satisfy a certain constraint.
Let's start on the next step!
Backtracking and Depth First Search
In very simple terms, we can think of backtracking as building and exploring a search tree in a depth first manner. The root node of the tree, or the "path" to the leaf node, represents a candidate solution that can be evaluated. So as we traverse through each path, we're testing a solution. So in the diagram below, A -> B -> D is one possible solution.
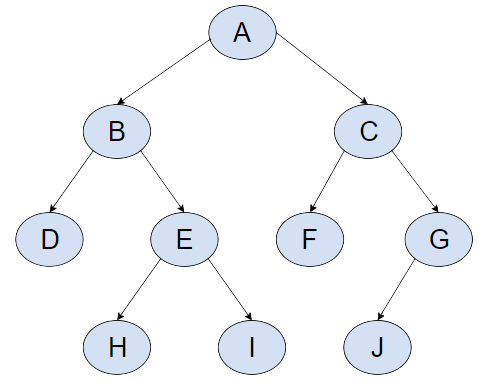
If the candidate path qualifies as a working solution, then it is kept as an alternative. Otherwise, the search continues in a depth first manner. In other words, once a solution is found, the algorithm backtracks (goes back a step, and explores another path from the previous point) to explore other tree branches to find more solutions.
Efficiency Gains
For constraint satisfaction problems, the search tree is "pruned" by abandoning branches of the tree that would not lead to a potential solution. Thus, we're constantly cutting down the search time and making it more efficient than an exhaustive or complete search. Let's now jump straight into how all of this is done via examples you might see on interview day.
Combinatorial Problem: Finding N Combinations
As a first problem, Iet's use a very simple problem from combinatorics-- can you find all possible N combinations of items from a set?
In other words, given a set {1, 2, 3, 4, 5} and an N value of 3, we'd be looking for all combinations/subsets of length/size 3. In this case, they would be {1, 2, 3}, {1, 2, 4}, and so on.
Note that the ordering is not important in a combination. so {1, 2, 3} and {3, 2, 1} are considered the same thing.
Let's now look at the pseudo-code for this N-combination problem:
xxxxxxxxxxroutine: combosinput: setoutput: display N combinationsassumption: position of the first item is zero and result set is empty at startbase case:1. If all combinations starting with items in positions < (size-N) have been printed. Stoprecursive case:Combos(set,result)1. Repeat for each items i in the set: a. Put the item i in the result set b. if the result set has N items, display it else recursively call combos with (the input set without item i) and (the result set) c. Remove the item i from result setImplementation of Combinatorial Solution
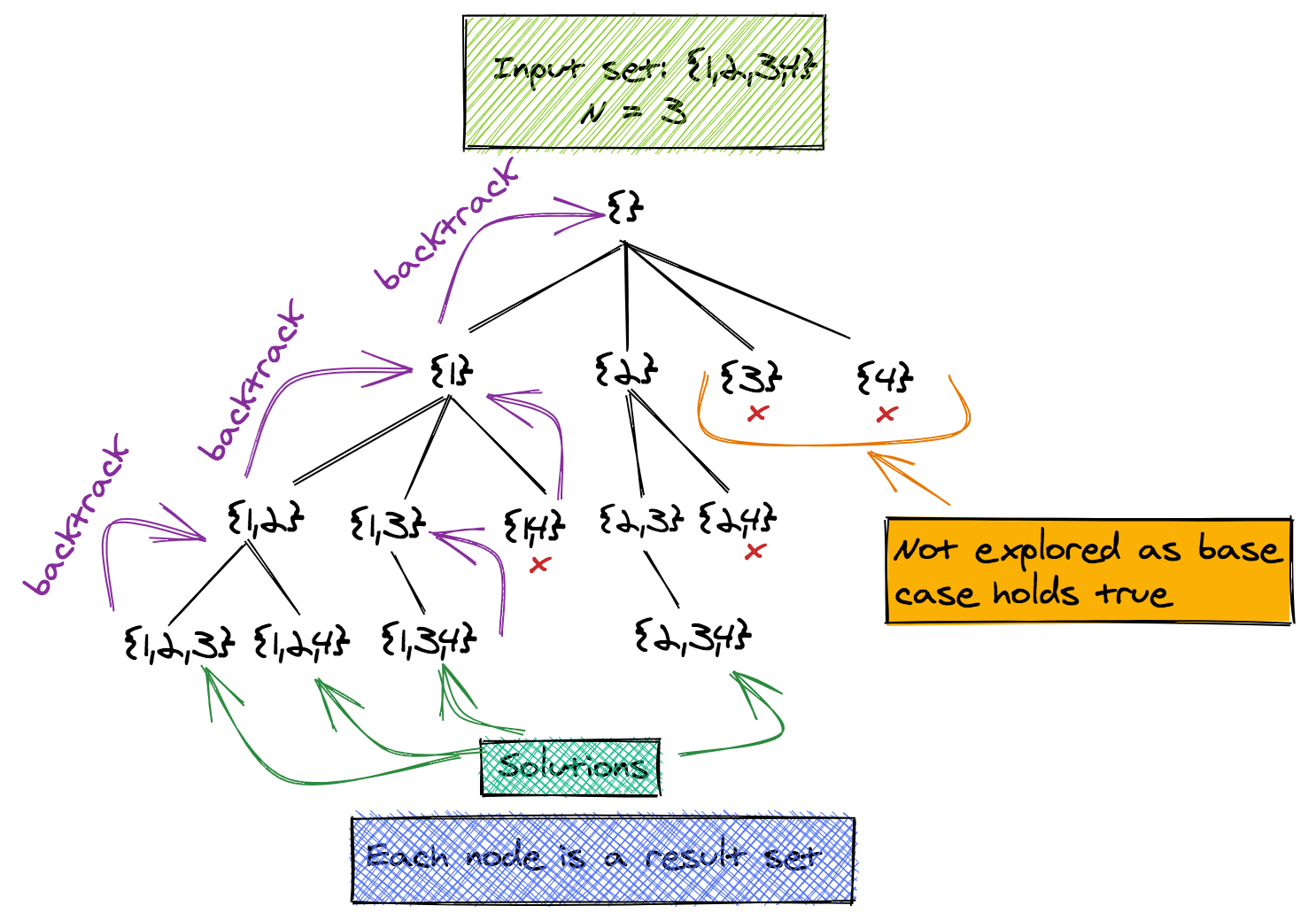
The diagram below shows how this pseudo code works for an input set {1, 2, 3, 4} and N=3.
Notice how the search tree is built from {} (empty set), to {1} to {1, 2} to {1, 2, 3}.
When {1, 2, 3} is found, the algorithm backtracks to {1, 2} to find all combinations starting with {1, 2}. Once that is finished the method backtracks to {1} to find other combinations starting with 1.
In this case, the entire search tree is not stored, but is instead built implicitly. Some paths, where the possibility of finding more combinations is not possible, are abandoned. The method is elegant and its C++ implementation is shown here.
Notice how in the base case 2 of the code, the exploration of combinations stops early on when the index of the set goes above a certain level. So in the tree above, the solutions {3} and {4} won't be explored. This is what makes the algorithm efficient.
xxxxxxxxxx}using namespace std;// helper: prints the vectorvoid printVector(vector<int>& arr){ cout << "\n"; for (int i = 0; i < arr.size(); ++i) cout << arr[i] << " "; cout << "\n";}// helper function:// prints all possible combinations of N numbers from a setvoid combosN(vector<int>& set, int N, vector<int>& result, int ind){ // base case 1 if (ind >= set.size()) return; // base case 2 if (result.size() == 0 && ind > set.size() - N) return; for (int i = ind; i < set.size(); ++i) { result.push_back(set[i]); if (result.size() == N) printVector(result); // print the result and don't go furtherCombinatorial Problem With A Constraint: Finding N Combinations with Sum < S
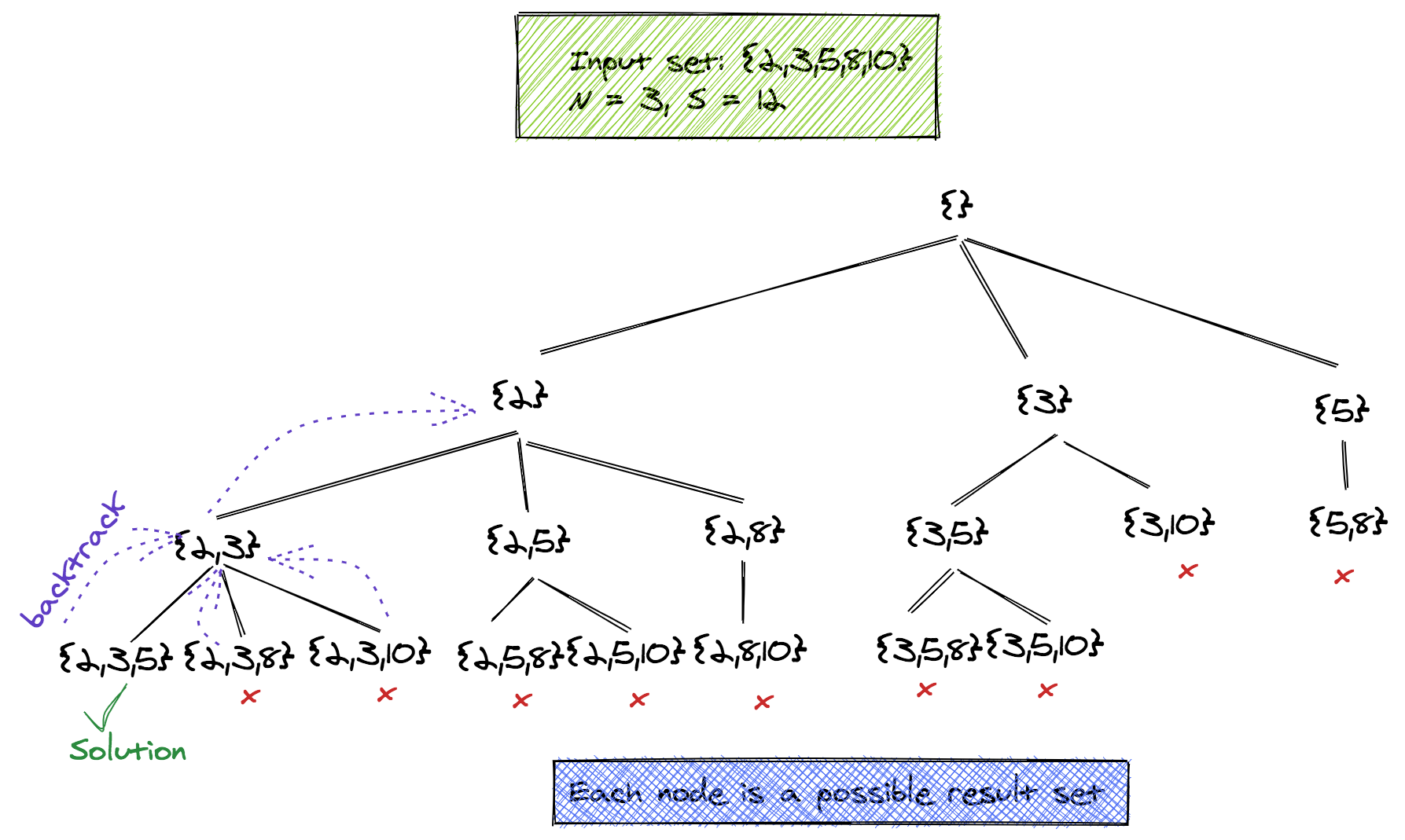
Let's now add a constraint to our N combinations problem! The constraint is-- that all sets where sum < S (S being a given parameter) should be printed out.
All we need to do is modify the combosN code, so that all combinations whose sum exceeds S are not explored further, and other such combinations are not generated. Assuming the array is sorted, it becomes even more efficient.
We've illustrated backtracking via arrays to keep things simple. This technique would work really well for unordered linked lists, where random access to elements is not possible.
The tree below shows the abandoned paths {3, 10} and {5, 8}.
xxxxxxxxxx// sum should be less than target of the argument. Rest is the same as combosN functionvoid combosNConstraint(vector<int>& arr, vector<int>& subsets, int ind, int target){ if (ind == arr.size()) return; for (int i = ind; i < arr.size(); ++i) { subsets.push_back(arr[i]); // do a recursive call only if constraint is satisfied if (sum(subsets) <= target) { printVector(subsets); combosNConstraint(arr, subsets, i + 1, target); } subsets.pop_back(); }}Enumerating Paths Through a Square Grid
Our next combinatorial problem is that of printing all possible paths from a start location to a target location.
Suppose we have a rectangular grid with a robot placed at some starting cell. It then has to find all possible paths that lead to the target cell. The robot is only allowed to move up or to the right. Thus, the next state is generated by doing either an "up move" or a "right move".
Backtracking comes to our rescue again. Here is the pseudo-code that allows the enumeration of all paths through a square grid:
xxxxxxxxxxroutine: enumeratePathsinput: Grid m*noutput: Display all pathsassumption: result is empty to begin withBase case 1:1. If target is reached then print the pathBase case 2:2. If left or right cell is outside the grid then stopRecursive case:1. Add the current cell to path2. Invoke enumeratePaths to find all paths that are possible by doing an "up" move3. Invoke enumeratePaths to find all paths that are possible by doing a "right" move4. Remove the current cell from pathSquare Grid Implementation
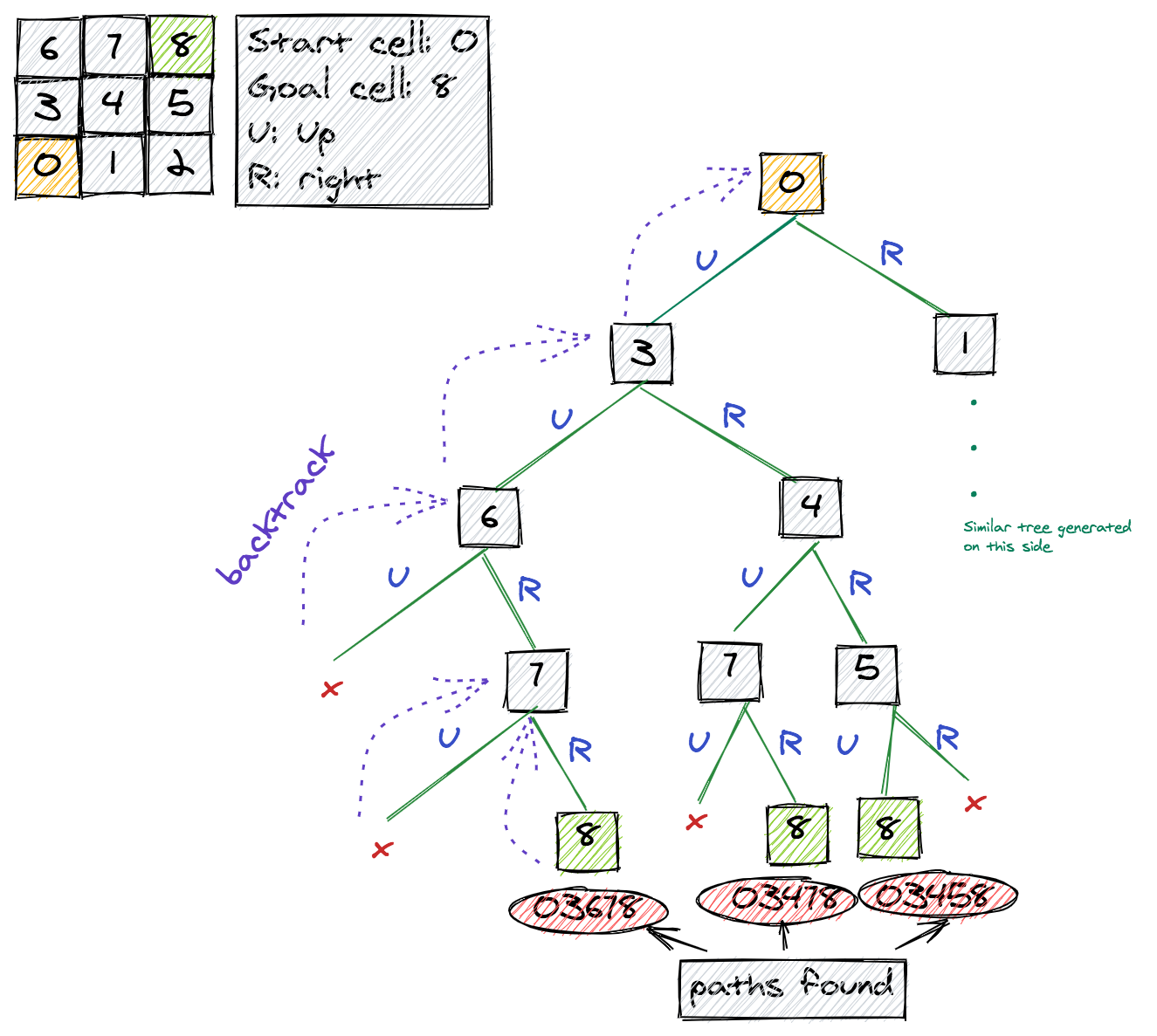
To see how the previous pseudo-code works, I have taken an example of a 3x3 grid and shown the left half of the tree. You can see that from each cell there are only two moves possible, i.e., up or right.
The leaf node represents the goal/target cell. Each branch of the tree represents a path. If the goal is found (base case 1), then the path is printed. If instead, base case 2 holds true (i.e., the cell is outside the grid), then the path is abandoned and the algorithm backtracks to find an alternate path.
Note: only a few backtrack moves are shown in the figure. However, after finding the goal cell, the system again backtracks to find other paths. This continues until all paths are exhaustively searched and enumerated.
The code attached is a simple C++ implementation of enumerating all paths through an m * n grid.
xxxxxxxxxx// helper recursive routinevoid enumeratePaths(int rows, int cols, vector < int > & path, int r, int c) { path.push_back(c + cols * r); // base case 1 if (r == rows - 1 && c == cols - 1) { printVector(path); return; } // base case 2 if (r >= rows) // out of bound. do nothing return; // base case 2 if (c >= cols) // out of bound. do nothing return; // row up enumeratePaths(rows, cols, path, r + 1, c); // backtrack path.pop_back(); // column right enumeratePaths(rows, cols, path, r, c + 1); path.pop_back();}// to be called by uservoid enumeratePathsMain(int rows, int cols) { vector < int > path; enumeratePaths(rows, cols, path, 0, 0);}Find Path Through a Maze
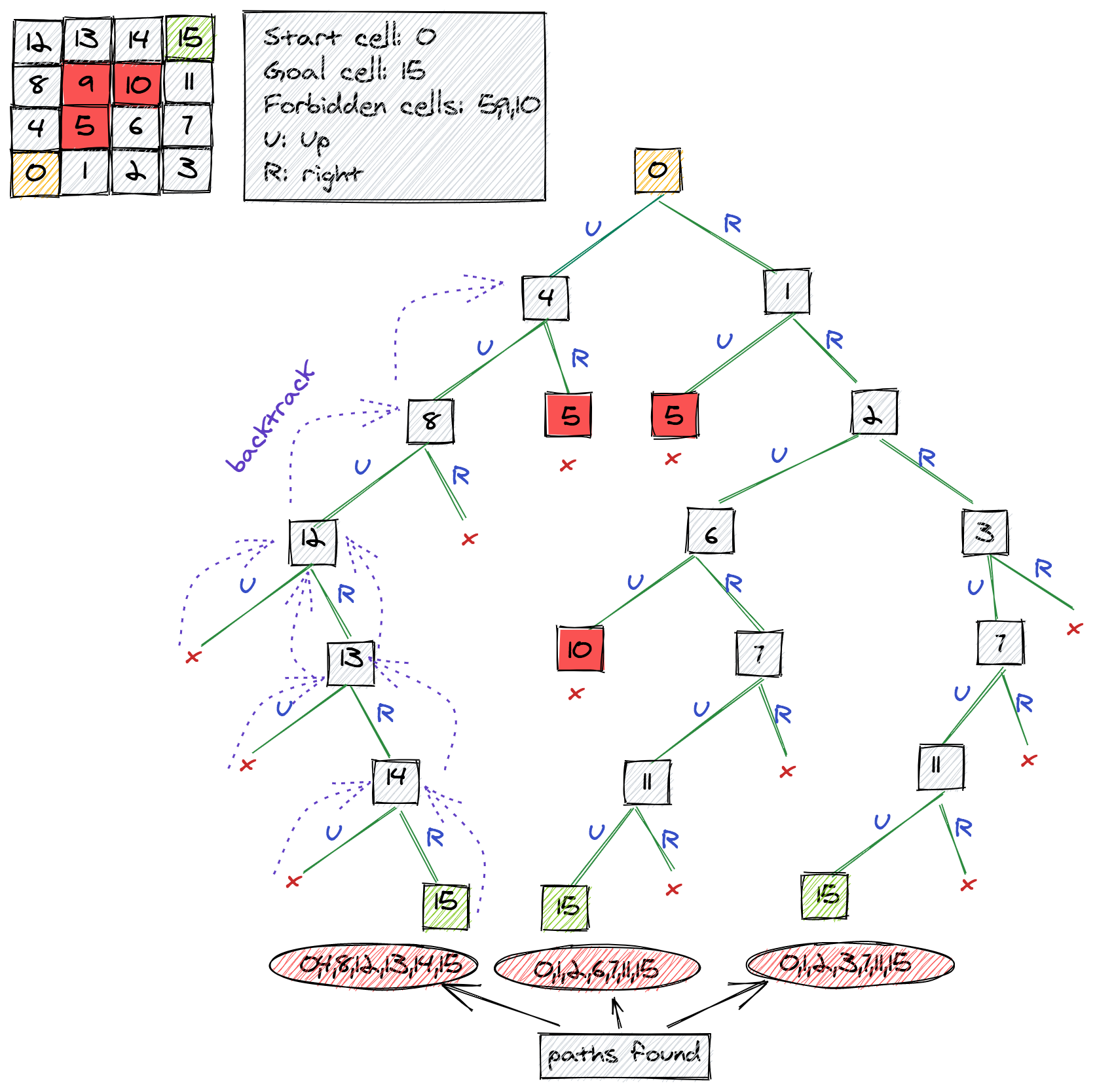
We can extend the prior problem to find the path through the maze. You can think of this problem as the grid problem, but with an added constraint. The constraint is this-- that some cells of the maze are not accessible at all, so the robot cannot step into those cells.
Let's call these "inaccessible" cell pits, where the robot is forbidden to enter. The paths that go through these cells should then be abandoned earlier on in "the search". The pseudo-code thus remains the same with one additional base case, which is to stop if the cell is a forbidden cell.
xxxxxxxxxxroutine: enumerateMazeinput: Grid m * noutput: Display all pathsassumption: result is empty to begin withBase case 1:1. If target is reached then print the pathBase case 2:2. If left or right cell is outside the maze then stopBase case 3:3. If the cell is a pit then stopRecursive case:1. Add the current cell to path2. Invoke enumerateMaze to find all paths that are possible by doing an "up" move3. Invoke enumerateMaze to find all paths that are possible by doing a "right" move4. Remove the current cell from pathThe figure below shows how paths are enumerated through a maze with pits. I have not shown all the backtracking moves, but the ones shown give a fairly good idea of how things are working. Basically, the algorithm backtracks to either a previous cell to find new paths, or backtracks from a pit to find new paths.
The C++ code attached is an implementation of enumerating all paths through a maze, which is represented as a binary 2D array. The main function that we can call is enumerateMazeMain and you can add a function to initialize the maze differently. The main recursive function translated from the above pseudo-code is the enumerateMaze function.
xxxxxxxxxx// m.enumerateMazeMain();class mazeClass { vector<vector<int> > maze; void enumerateMaze(vector<int>& path, int r, int c) { path.push_back(c + maze.size() * r); // base case 1 if (r == maze.size() - 1 && c == maze[0].size() - 1) { printVector(path); return; } // base case 2 if (r >= maze.size()) // out of bound. do nothing return; // base case 2 if (c >= maze.size()) // out of bound. do nothing return; // base case 3 if (!maze[r][c]) return; // row up enumerateMaze(path, r + 1, c); // backtrack path.pop_back(); // column right enumerateMaze(path, r, c + 1); path.pop_back();Solving Sudoku
The last example in this tutorial is coming up with a solution to one of my favorite combinatorial games-- Sudoku-- via backtracking!
Sudoku is a classic example of a problem with constraints, which can be solved via backtracking. It works like magic! To simplify the problem, let's use an easier version of the sudoku game.
We can model the game as an N * N grid, each cell having numbers from 1 .. N.
The rule is not to repeat the same number in a column or row. The initial sudoku board has numbers in some cells, and are empty for the rest. The goal of the game is to fill out the empty cells with numbers from 1 .. N, so that the constraints are satisfied. Let us now look at how backtracking can be used to solve a given Sudoku board.
xxxxxxxxxxRoutine: solveInput: Sudoku boardRule: No repetition of a number in the same row or columnAssumption: The initial board configuration is according to Sudoku rulesBase case:1. If all empty places are filled return success2. If all combinations are tried and the board is invalid, return falseRecursive case (returns success or failure):1. Choose an empty cell2. For each candidate number i in the range 1..N a. Place the candidate i in the empty cell b. Check if the board is valid with candidate i. If the board is valid, then { i. result = invoke the solve routine on the next empty cell ii. If result is true then stop and return success } else Continue with the next candidate as given in step 23. return failure (no possible combination is possible)Results
It's pretty awesome that we can actually find a solution to Sudoku via a simple backtracking routine. Let's see this routine in action on a simple 4 x 4 board as shown in the figure below. There are three empty cells. We can see that all combinations of numbers are tried.
Once an invalid board configuration is found, the entire branch is abandoned, backtracked, and a new solution is tried. The C++ implementation is provided. You can add your own public function to initialize the board differently.
xxxxxxxxxx// s.print();class sudoku { vector<vector<int> > board; void Initialize() { int arrBoard[] = { 2, 1, 3, 4, 1, 3, -1, 2, -1, 2, -1, 3, -1, -1, 2, 1 }; vector<int> temp; int ind = 0; for (int i = 0; i < 4; i++) { temp.clear(); for (int j = 0; j < 4; ++j) {Take Away Lesson
Backtracking is a very important principle that every software engineer should be aware of, especially for interviews. You should use it when you need to enumerate all solutions of a problem. Take advantage of it in scenarios where the solutions required have to satisfy a given constraint.
But before applying backtracking blindly to a problem, think of other possible solutions and consider how you can optimize your code. As always, work things out on a piece of paper with a pen (or with pseudocode!), rather than directly jumping into code.
Try this exercise. Click the correct answer from the options.
Given this pseudo-code for the N combinations problem:
1base case:
21. If all combinations starting with items in positions < (size-N) have been printed. Stop
3
4recursive case:
5Combos(set, result)
61. Repeat for each items i in the set:
7 a. Put the item i in the result set
8 b. if the result set has N items, display it
9 else
10 recursively call combos with (the input set without item i) and (the result set)
11 c. Remove the item i from result setWhat should you change in the code above if all possible combinations of any size are to be displayed?
Click the option that best answers the question.
- Change step a of Combos routine with N items in set
- Change step b of Combos and display the set unconditionally
- Remove step c of Combos
- None of these options
Are you sure you're getting this? Click the correct answer from the options.
For the path problem through a grid, how many possible paths are there for a 5x5 grid if the start position is (0,0) and the goal is (4,4)?
Click the option that best answers the question.
- 64
- 70
- 32
- None of the above
One Pager Cheat Sheet
Backtrackingis a powerful algorithm used to explore all potential solutions to a problem and identify those that satisfy aconstraint, making it a useful tool for Combinatorial, Path Finding, and Sudoku Solving.- The algorithm of
backtrackingcreates asearch treeand explores it in a depth first manner to find candidate solutions that can be pruned to become more efficient. - Finding all possible combinations of items from a set of size
Nis an example of acombinatoricsproblem that can be solved with a pseudo code solution. - The algorithmic solution builds an implicit search tree starting with an empty set, and explores certain paths while abandoning others in order to find all possible combinations in an efficient manner.
- We can modify our
combosNcode to find allNcombinations whosesum < S, with an even more efficient version when the array is sorted. - We can use
backtrackingto enumerate all possible paths from astartlocation to atargetlocation in a square grid by making alternating "up" and "right" moves. - By backtracking through all possible paths of an
m * ngrid, this code provides a simple C++ implementation to list out all paths from a given cell, and prints them if they reach thegoal/targetcell. - Find a
paththrough amazeby abandoning earlier on in the search any paths leading to cells forbidden to the robot. - The C++ code implements an algorithm which
backtracksfrom pits or previous cells to enumerate all paths through a binary 2D array, which serves as a representation of the maze. - Solving
Sudokuinvolves usingbacktrackingto fill out anN * Ngrid with numbers from1 .. Nso that no row or column contains a repeated number. - We can solve Sudoku using a simple backtracking routine and an accompanying
C++ implementation. - Backtracking is an important technique for enumerating all possible solutions satisfying a given constraint and
software engineersshould beware of its complexity and carefully plan how to optimize their code before using it. - Step b of
Combosshould be changed to unconditionally display the set and no additional checks should be made to determine the size, so that all possible combinations of any size can be printed. - There are 70 distinct paths between
(0,0)and(4,4)in a5x5grid, which can be calculated using the factorial formula to calculate the number of ways to arrange the 24 distinct paths that must be traveled.