Implementation of Combinatorial Solution

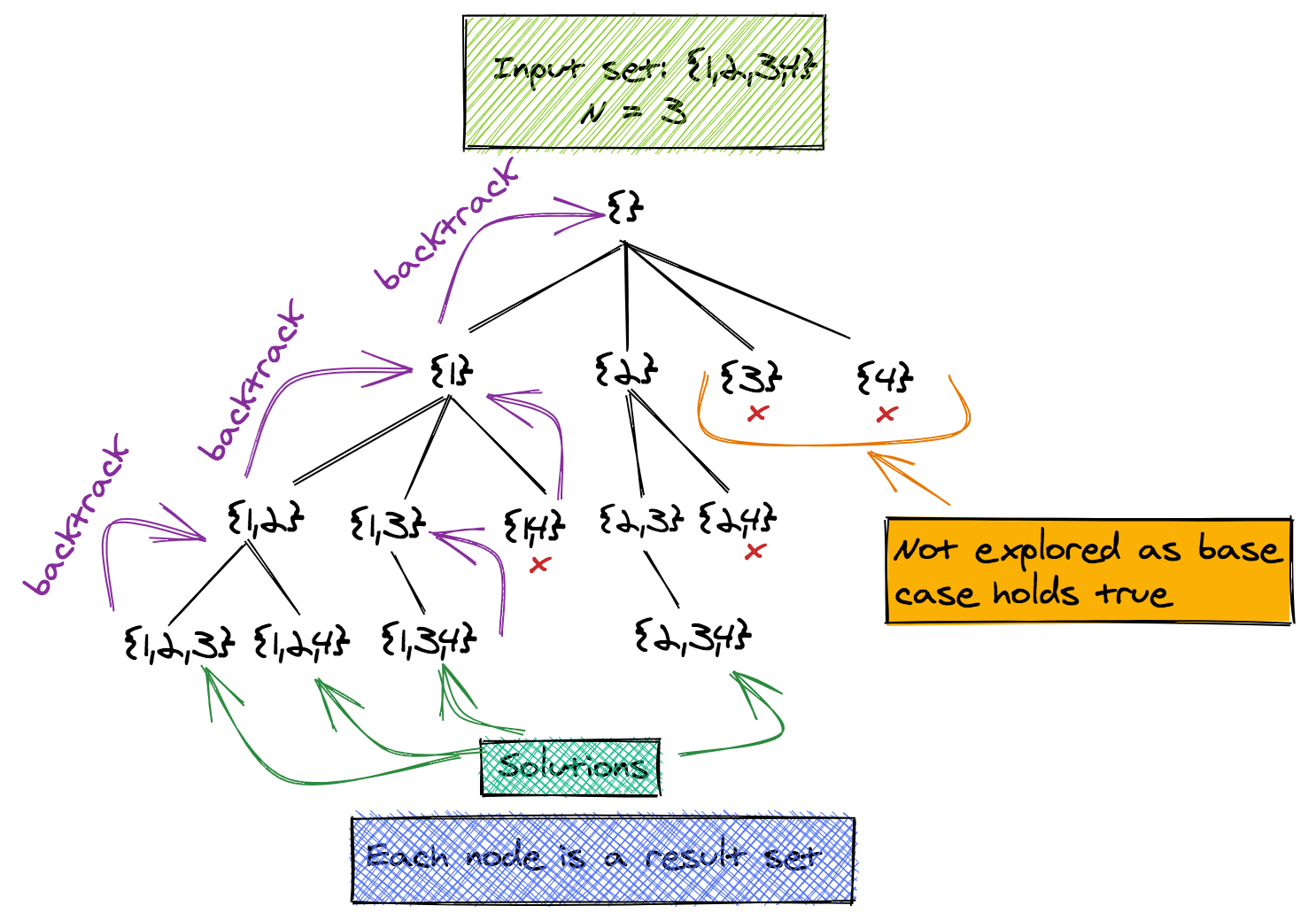
The diagram below shows how this pseudo code works for an input set {1, 2, 3, 4} and N=3.

Notice how the search tree is built from {} (empty set), to {1} to {1, 2} to {1, 2, 3}.

When {1, 2, 3} is found, the algorithm backtracks to {1, 2} to find all combinations starting with {1, 2}. Once that is finished the method backtracks to {1} to find other combinations starting with 1.

In this case, the entire search tree is not stored, but is instead built implicitly. Some paths, where the possibility of finding more combinations is not possible, are abandoned. The method is elegant and its C++ implementation is shown here.

Notice how in the base case 2 of the code, the exploration of combinations stops early on when the index of the set goes above a certain level. So in the tree above, the solutions {3} and {4} won't be explored. This is what makes the algorithm efficient.

xxxxxxxxxx

}

#include <iostream>

#include <vector>

#include <string>

​

using namespace std;

​

// helper: prints the vector

void printVector(vector<int>& arr)

{

    cout << "\n";

    for (int i = 0; i < arr.size(); ++i)

        cout << arr[i] << " ";

    cout << "\n";

}

​

// helper function:

// prints all possible combinations of N numbers from a set

void combosN(vector<int>& set, int N, vector<int>& result, int ind)

{

    // base case 1

    if (ind >= set.size())

        return;

    // base case 2

    if (result.size() == 0 && ind > set.size() - N)

        return;

    for (int i = ind; i < set.size(); ++i) {

        result.push_back(set[i]);

        if (result.size() == N)

            printVector(result); // print the result and don't go further