Square Grid Implementation

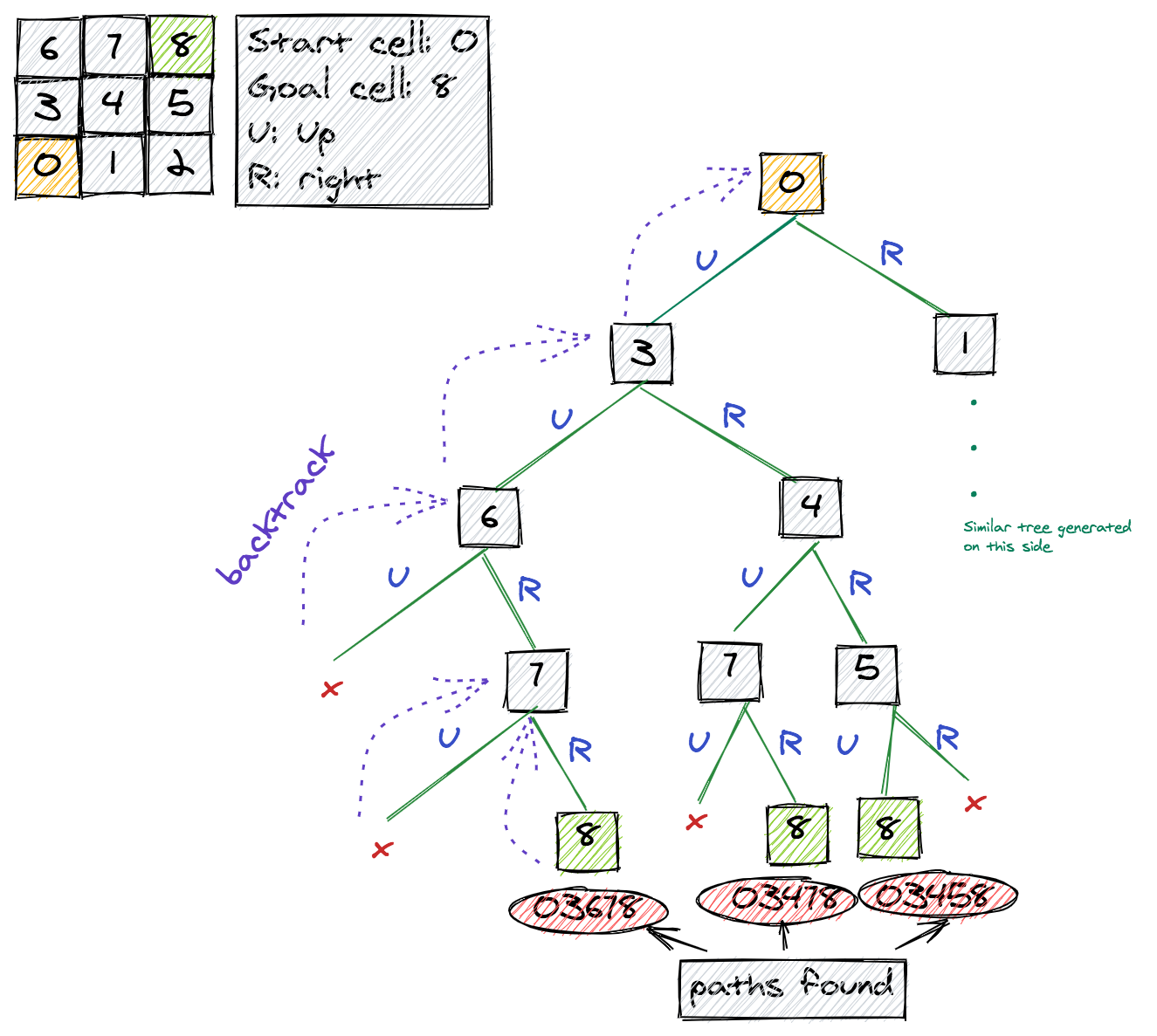
To see how the previous pseudo-code works, I have taken an example of a 3x3 grid and shown the left half of the tree. You can see that from each cell there are only two moves possible, i.e., up or right.

The leaf node represents the goal/target cell. Each branch of the tree represents a path. If the goal is found (base case 1), then the path is printed. If instead, base case 2 holds true (i.e., the cell is outside the grid), then the path is abandoned and the algorithm backtracks to find an alternate path.

Note: only a few backtrack moves are shown in the figure. However, after finding the goal cell, the system again backtracks to find other paths. This continues until all paths are exhaustively searched and enumerated.

The code attached is a simple C++ implementation of enumerating all paths through an m * n grid.

xxxxxxxxxx

// helper recursive routine

void enumeratePaths(int rows, int cols, vector < int > & path, int r, int c) {

​

  path.push_back(c + cols * r);

  // base case 1

  if (r == rows - 1 && c == cols - 1) {

    printVector(path);

    return;

  }

  // base case 2

  if (r >= rows) // out of bound. do nothing

    return;

  // base case 2

  if (c >= cols) // out of bound. do nothing

    return;

​

  // row up

  enumeratePaths(rows, cols, path, r + 1, c);

  // backtrack

  path.pop_back();

  // column right

  enumeratePaths(rows, cols, path, r, c + 1);

  path.pop_back();

}

// to be called by user

void enumeratePathsMain(int rows, int cols) {

  vector < int > path;

  enumeratePaths(rows, cols, path, 0, 0);

}