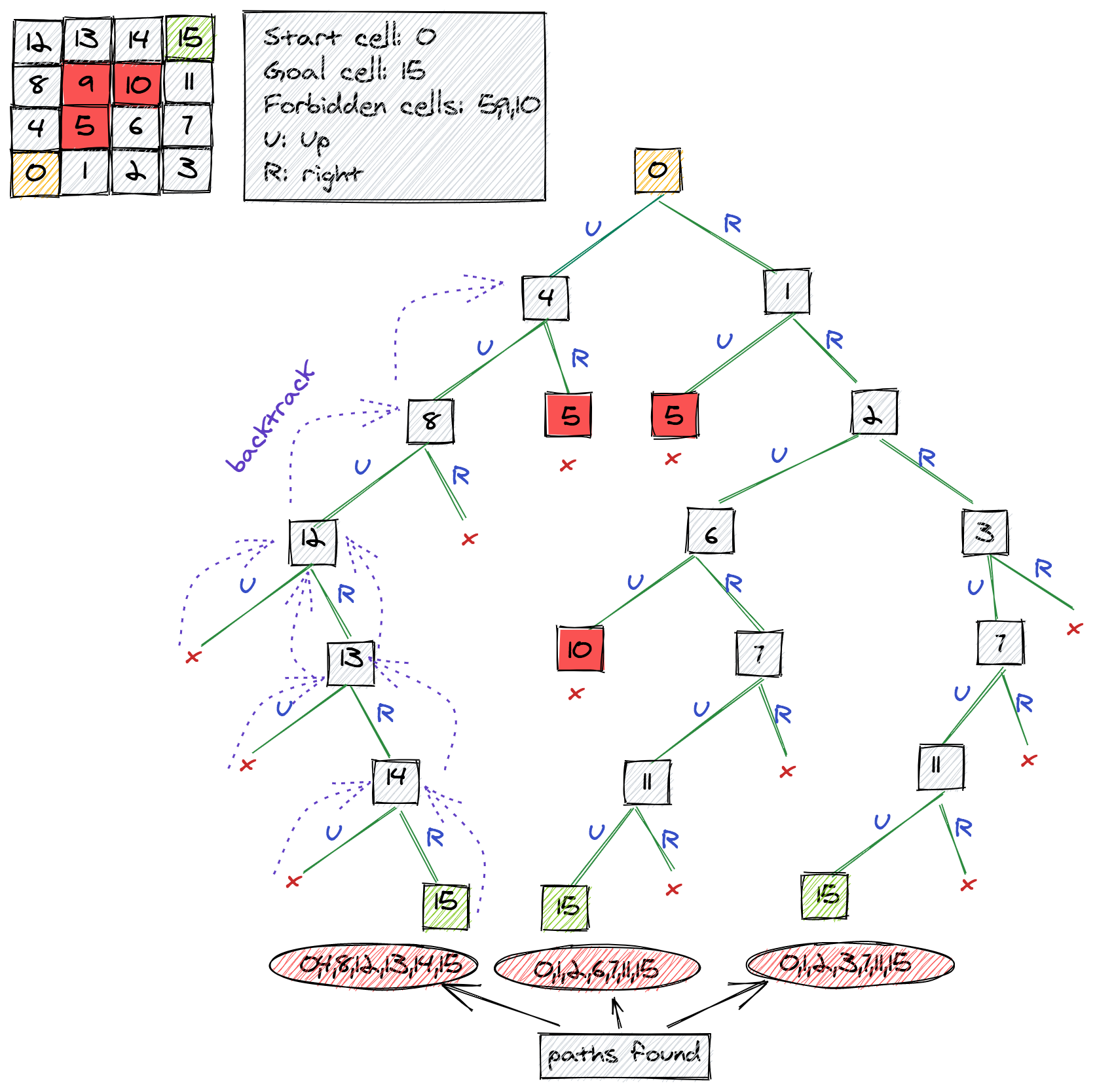
The figure below shows how paths are enumerated through a maze with pits. I have not shown all the backtracking moves, but the ones shown give a fairly good idea of how things are working. Basically, the algorithm backtracks to either a previous cell to find new paths, or backtracks from a pit to find new paths.
The C++ code attached is an implementation of enumerating all paths through a maze, which is represented as a binary 2D array. The main function that we can call is enumerateMazeMain and you can add a function to initialize the maze differently. The main recursive function translated from the above pseudo-code is the enumerateMaze function.
xxxxxxxxxx79
// m.enumerateMazeMain();class mazeClass { vector<vector<int> > maze; void enumerateMaze(vector<int>& path, int r, int c) { path.push_back(c + maze.size() * r); // base case 1 if (r == maze.size() - 1 && c == maze[0].size() - 1) { printVector(path); return; } // base case 2 if (r >= maze.size()) // out of bound. do nothing return; // base case 2 if (c >= maze.size()) // out of bound. do nothing return; // base case 3 if (!maze[r][c]) return; // row up enumerateMaze(path, r + 1, c); // backtrack path.pop_back(); // column right enumerateMaze(path, r, c + 1); path.pop_back();OUTPUT
:001 > Cmd/Ctrl-Enter to run, Cmd/Ctrl-/ to comment