What Is Integer Overflow?
Integer overflow or wraparound occurs when we store a value that is larger than the space available for storing this value.
A Simple Example
A simple example can be understood by considering an char variable in Java. Java reserves 16 bits for the char variable, so it can store values ranging from 0 to 65535. In the code below, we'll display the value of the variable as an integer to see exactly what it is storing.
1var a;
2a = 0xffff; //Set all bits to 1
3console.log("Original: " + a);
4a++;
5console.log("After increment: " + a);The output you'll see is:
1Original: 65535
2After increment: 0(base)A programmer not aware of this problem was expecting the variable a set to 65536. Instead, a wrap around occurred.
What Is A WrapAround?
Let's understand what is going on when arithmetic is performed on integers. When a=65535, the 16 bit variable stores this in binary as: 0b1111111111111111 (or 0xffff in hex). When a one is added to this, the correct result would be 0b10000000000000000 in binary (or 0x010000). However, only the 16 least significant bits would be stored, so the most significant bit containing the one is lost and we are left with all zeros; and hence the final result we see is 0. This is known as a wraparound problem resulting from the loss of the most significant digits of the result of an arithmetic operation.
To know the exact result stored in an integer variable from a wraparound when value 'v' is stored in an integer variable, which is n bits long, the following formula can be used:
1result stored from overflow = v modulo 2^nIf v is in the range of the variable, the result stored would be v, otherwise it is reduced to the last n least significant bits.

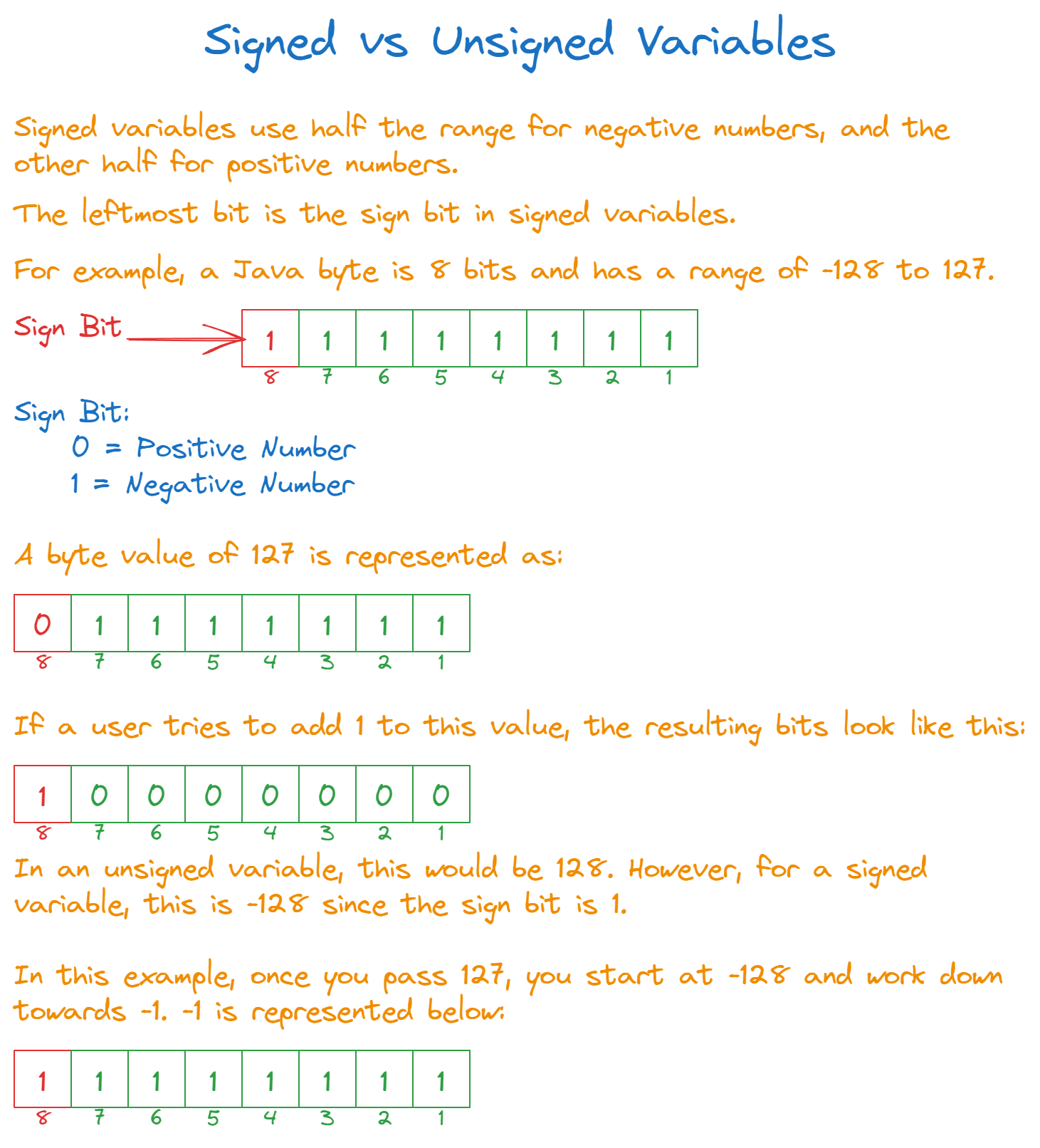
Signed Vs. Unsigned Confusion
Another major issue is the signed vs. unsigned type mixup. There are no unsigned types in Java, but other languages like C++ support them. Let's look at the example below, where we have a byte type variable x. The byte data type in Java is 8 bits and supports a range from -128 to +127. Any programmer can easily fall into the trap by not considering that half the range belongs to negative number and half of it is reserved for positive numbers.
1var x = 127;
2console.log("Original: " + x);
3x++;
4if (x > 127) x -= 256; // Simulate byte overflow
5console.log("After increment: " + x);The output is:
1Original: 127
2After increment: -128Again, here we can see that adding one to 127 has led to a value of -128. Here, the reason is the way negative numbers are stored. The binary number 0b10000000 is actually the representation of -128. If the most significant bit is one, then the number is a negative number.