Mark As Completed Discussion

Good morning! Here's our prompt for today.

Let's build a very basic calculator by programming it! You've probably seen one that look similar to this:

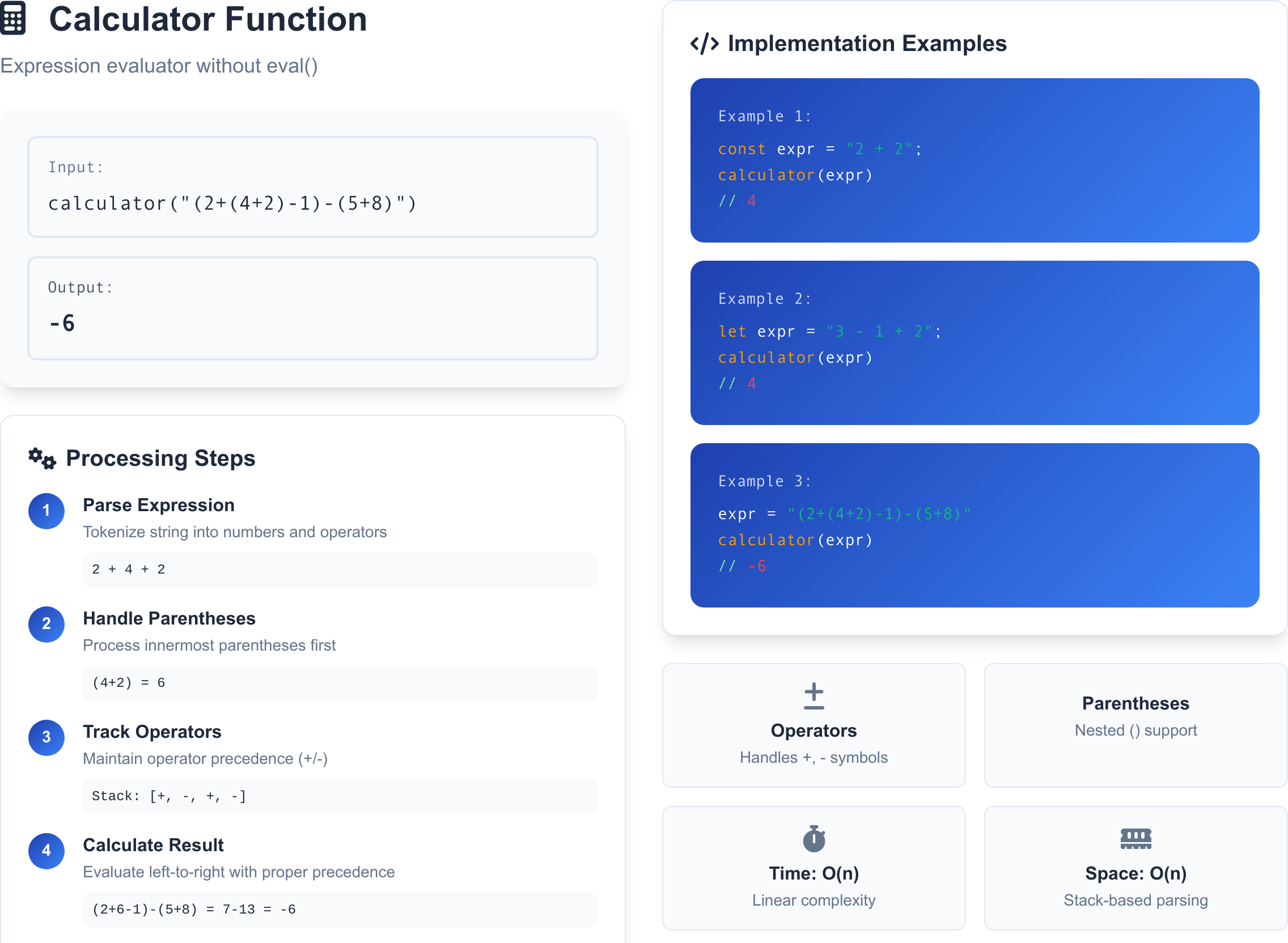
Description

But we won't be building a physical calculator (HardwareDaily will need to wait!)-- instead, we'll be writing a simple program that can serve as one. Can you write a function that will evaluate a simple expression string without using your language's eval method?

1const expr = "2 + 2";
2calculator(expr)
3// 4

It should also be able to handle positive and negative symbols +,-, parentheses (), and spaces.

1let expr = "3 - 1 + 2";
2calculator(expr)
3// 4
4
5expr = "(2+(4+2)-1)-(5+8)"
6calculator(expr)
7// -6

Assume for now that you don't need to handle multiplication or division cases.

Constraints

  • Length of the given string <= 100000
  • The numbers present in the string will be a single digit number
  • Expected time complexity : O(n)
  • Expected space complexity : O(n)

Try to solve this here or in Interactive Mode.

How do I practice this challenge?

RUN CODERESET SAVE
CSHARP
OUTPUT
:001 > Cmd/Ctrl-Enter to run, Cmd/Ctrl-/ to comment

Here's how we would solve this problem...

How do I use this guide?

Setting the Stage: The Art of Mathematical Evaluation

Calculators, those nifty little devices that have saved us during countless math classes. But what if we could replicate that magic in software?

The idea is to build a "software calculator" that can evaluate mathematical expressions. Our goal is to evaluate expressions like 2 + 2 and (2+(4+2)-1)-(5+8) without using the built-in eval function in any language.

Why Skip the eval Function?

You might wonder, "If there's a built-in way to evaluate code strings, why not just use it?" Well, that's a great question! The eval function is quite handy, but it has its drawbacks:

  • Security Risks: Using eval can expose your code to security vulnerabilities.
  • Limited Customization: What if you want to extend the calculator functionality? With eval, you're stuck with what the language offers.
  • Learning Opportunity: Building our own calculator is an excellent exercise for understanding parsing and evaluation algorithms.

How eval Works, Anyway?

Just to give you an idea, if we were to use eval, you could evaluate an expression like this:

1// C# has no direct `eval` function but can compile code at runtime using libraries like Roslyn
2using Microsoft.CodeAnalysis.CSharp.Scripting;
3using Microsoft.CodeAnalysis.Scripting;
4using System;
5
6class Program {
7    static async Task Main() {
8        try {
9            var result = await CSharpScript.EvaluateAsync("1+1");
10            Console.WriteLine(result);
11        } catch (CompilationErrorException compilationError) {
12            // Handle error
13        }
14    }
15}

Thinking Like a Compiler

We can't use the built-in eval method, but that's not going to stop us.

Thinking Like a Compiler

Let's put on our compiler hats and dissect this problem. Essentially, our job is to translate the language of mathematics into something the machine understands. Our plan involves two critical steps:

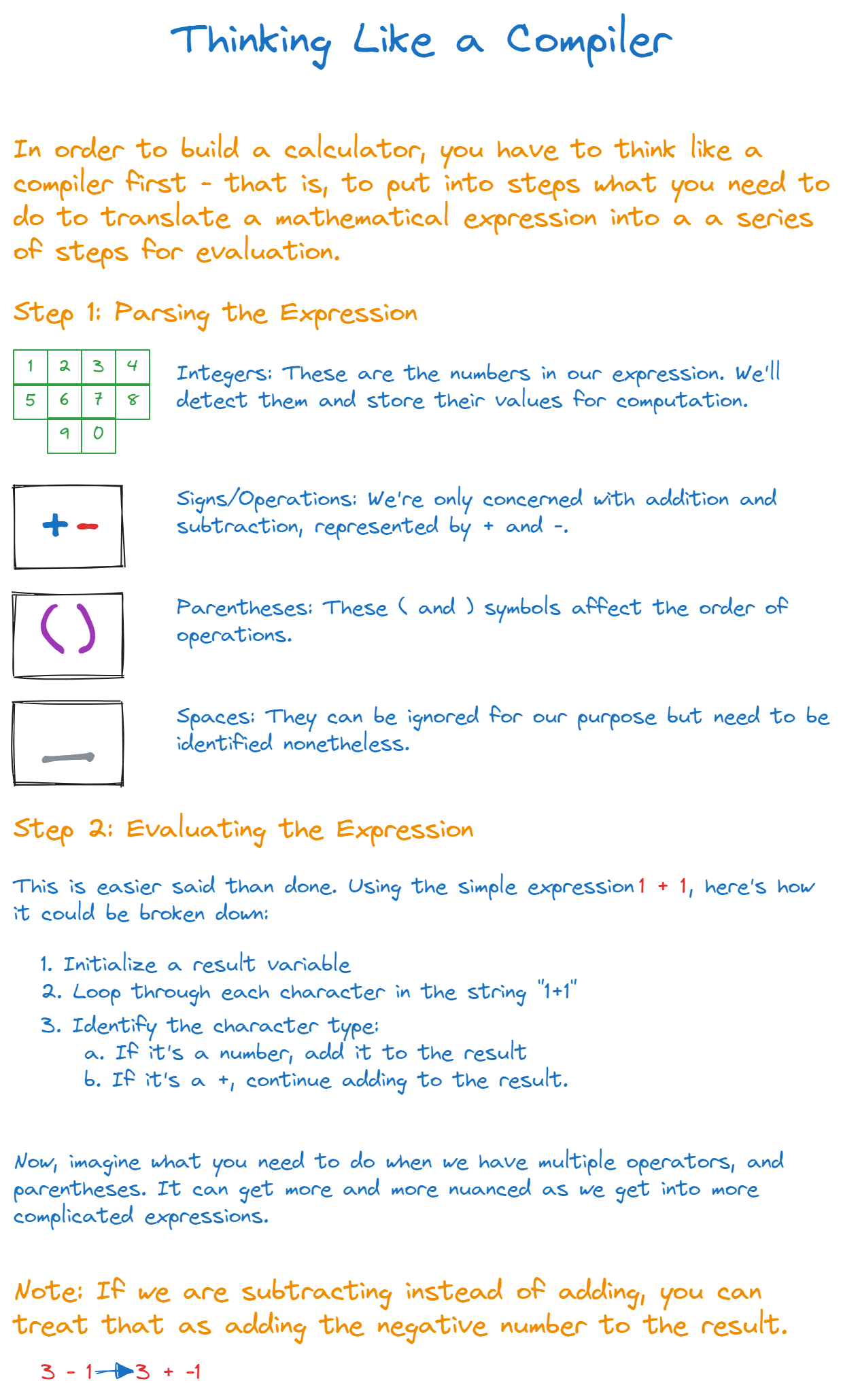
Step 1: Parsing the Expression

In this step, we're essentially acting as translators. We must walk through each character in the expression string and categorize it. Think of it as scanning a sentence and tagging each word as a noun, verb, or adjective. In our case, we have four types of "words" or symbols:

  1. Integers: These are the numbers in our expression. We'll detect them and store their values for computation.
  2. Signs/Operations: We're only concerned with addition and subtraction, represented by + and -.
  3. Parentheses: These ( and ) symbols affect the order of operations.
  4. Spaces: They can be ignored for our purpose but need to be identified nonetheless.

Step 2: Evaluating the Expression

Once we know what each symbol stands for, we can proceed to do the actual math. This is the part where we apply the rules of arithmetic to get our final answer.

Crafting a Strategy

Our roadmap seems pretty straightforward; however, there are some "watch out!" signs along the way. The devil is in the details—or in this case, the order and combination of these symbols.

A Simple Example: '1+1'

Let's use the simple expression 1+1 to illustrate our approach. Imagine a variable result that stores the outcome. Now, our logic could look like this:

  1. Initialize result to 0.
  2. Loop through each character in the string '1+1'.
  3. Identify the character type:
  • If it's a number, add it to result.

  • If it's a +, continue adding to result.

Our logic flows naturally, but as we'll discover, more complex expressions will require a more nuanced approach.

1using System;
2
3class Program {
4    static void Main() {
5        string expression = "1+1";
6        int result = 0;
7
8        foreach (char c in expression) {
9            if (Char.IsDigit(c)) {
10                result += (int)Char.GetNumericValue(c);
11            }
12            // If it's a '+', we simply continue the loop
13        }
14        Console.WriteLine("Result: " + result);
15    }
16}

The Elegance of Addition

Addition is straightforward, isn't it? When we encounter a number in our expression string, we simply add it to our running total, which we'll call result. That's about it for addition.

Subtraction as "Negative Addition"

Here's where the subtlety comes in. Instead of thinking of subtraction as a separate operation, let's reframe it as adding a negative number. This concept simplifies our logic beautifully. Now, we don't have to juggle between two different operations; it's all addition!

A Practical Example: '1-1'

To illustrate how this works, let's consider the expression 1-1. Our logic could flow as follows:

  1. Initialize result to 0.
  2. Loop through each character in the string '1-1'.
  3. Identify what each character is:
  • If it's a number, add it to result.
  • If it's a - sign, prepare to make the next number negative.

By following these steps, we'll add 1 to result, and then effectively add -1 to result, resulting in a final value of 0.

In the above example, we simply converted the signage when we encountered a minus symbol-- so we need to keep some concept of what sign we're at. This will allow us to keep track of what operation we're performing, whether it's + or -.

Assuming we handle signage with a 1 or a -1, our method so far starts to look something like this:

RUN CODERESET
CSHARP
OUTPUT
:001 > Cmd/Ctrl-Enter to run, Cmd/Ctrl-/ to comment

Parentheses

Parentheses serve a dual role: they dictate the order of operations, and in more complex scenarios, they could also signify multiplication. But we're ignoring multiplication for now. So, what's the big deal?

Parentheses

Why Are Parentheses Tricky?

Parentheses create a new "scope" for our calculations. Think of them like those Russian nesting dolls; what happens inside the innermost doll shouldn't affect the outer dolls directly. Parentheses introduce a hierarchical structure to the expression, which complicates our otherwise linear flow of calculations.

The Mighty Stack Data Structure

The classic way to handle this hierarchical structure is by using a stack. Imagine a stack of books; you can only add or remove a book from the top. Similarly, a stack in computer science is a data structure where you can add elements to the top and remove them from the top.

We'll use two stacks for our calculator:

  1. Result Stack: To keep track of intermediate results.
  2. Operation Stack: To store the sign (either + or -) before and within the parentheses.

Logic for Handling Parentheses

The stack will help us remember the result and sign right before we enter a new set of parentheses. When we close the parentheses, we can pop the top elements from our stacks to restore the previous state and correctly compute the result.

1if (curr == '(') {
2    stack.Push(result);
3    result = 0;
4    operationStack.Push(sign);
5    sign = 1;
6} else if (curr == ')') {
7    result = operationStack.Pop() * result + stack.Pop();
8    sign = 1;
9}

By using stacks to manage the state inside parentheses, we can effectively simplify our calculations while respecting the order of operations. So, are you ready to integrate this into our calculator code?

One final caveat-- we also need to handle spaces, but that's easy to accomplish by skipping that iteration.

1if (curr == ' ') {
2    continue;
3}

Complexity of Final Solution

Let n be the length of the input. We iterate through the input once for O(n) time complexity, and we can have up to n elements on the stack (for example having an input only containing () for O(n) space complexity as well.

Let's see it all together now.

The Multiplication and Division Conundrum

So, you've mastered addition, subtraction, and those tricky parentheses. Feeling confident?

Now, let's up the ante with multiplication and division. This is often the follow-up question in interviews, and it adds an extra layer of complexity. Why? Because multiplication and division have higher precedence than addition and subtraction, and they introduce non-linear relationships between the numbers.

The Fundamental Question: Why Stacks?

The stack is a lifeline in this problem for one primary reason: it provides a way to handle different priorities of operations without needing to backtrack. Think of it as a holding area or a waiting room where numbers and operations can wait their turn to be processed in the correct sequence.

Why Does a Stack Work?

A stack works on a last-in, first-out (LIFO) principle. It allows us to temporarily "park" elements that we'll need soon but not immediately. In the case of multiplication and division, this "parking" facility becomes invaluable. It enables us to first collect the operands and then perform the operation when the time is right.

Mental Model with Example: "4 * 3 + 2"

Let's take an example expression: 4 * 3 + 2. There's no parentheses, so it's easier to follow. We'll use Python for this example.

Here's a step-by-step breakdown:

  1. Initialization: We initialize num to 0, stack to an empty list, and sign to +.
1int num = 0;
2Stack<int> stack = new Stack<int>();
3char sign = '+';

  1. First Iteration (4):

    • We encounter 4, so num becomes 4.

  2. Second Iteration (*):

    • We hit the *. At this point, the previous sign was +, so we push 4 onto stack.
    • We update sign to *.

  3. Third Iteration (3):

    • We encounter 3, so num becomes 3.

  4. Fourth Iteration (+):

    • We hit the +. The last sign was *, so we pop 4 from stack and push 4 * 3 = 12.
    • We update sign to +.

  5. Fifth Iteration (2):

    • We encounter 2, so num becomes 2.

  6. End of String:

    • The last sign is +, so we push 2 onto stack.

  7. Final Calculation:

    • We sum the stack [12, 2], which results in 14.
RUN CODERESET
CSHARP
OUTPUT
:001 > Cmd/Ctrl-Enter to run, Cmd/Ctrl-/ to comment

Multiplication and Division with Parentheses

We've been focusing on adding and subtracting, but now let's tackle multiplication and division when they're tossed into the mix with parentheses. The challenge is to keep processing our string expression from left to right while still honoring the parentheses and the order of operations. So, let's rethink our approach a bit.

The "Aha" Moment: View Multiplication as Extended Addition

Imagine you're staring at the expression "4*(3+2)". We naturally get drawn to the parentheses and think about tackling that first. But what if we reframe it? Instead of seeing it as "4 multiplies (3+2)", think of it as "0 add (4 * 5)".

Why the Reframe Works

This reframe works because it turns a nested operation into a linear one. The operation that seemed nested within the parentheses is now another operation in the queue. And because we've flattened it out, we can handle it with a left-to-right pass through the string, just like we did with simpler expressions.

Leveraging the Stack for this Reframe

The stack data structure comes to our rescue here. As we go through the string, we keep track of numbers and operations, as usual. But now, when we encounter a parenthesis, we use the stack to "remember" the operation that was happening right before we dove into the parenthesis. This enables us to "flatten" the nested operation into a linear one.

PYTHON
1if ch == "(":
2    # We can still leverage the stack that we're using
3    # by recreating the parentheses expression within the stack
4    stack.append(sign)
5    stack.append('(')
6    # Reset to plus to add the parentheses expression results
7    sign = '+'

Unpacking the Parentheses

When we exit the parenthesis, we unpack the operations and numbers we've stored and perform the calculation. This way, the result of "3+2" in "4*(3+2)" becomes just another number in our queue of operations.

PYTHON
1if ch == ')':
2    # Complete our parentheses expression 
3    num, item = 0, stack.pop()
4    while item != '(':
5        num += item
6        item = stack.pop()
7    sign = stack.pop()

Python: Implementing the Strategy

With Parentheses

In Python, let's walk through the code step-by-step:

  1. Initialize Variables: We start by initializing our variables. The variable num will hold the number we're currently parsing, stack will hold our numbers and signs, and sign will hold the current operation (addition by default).

    PYTHON
    1num, stack, sign = 0, [], "+"

  2. Loop Through the String: We'll loop through each character in the string. For the last iteration, we append a '+' to ensure we process all numbers.

    PYTHON
    1for i, ch in enumerate(s + '+'):

  3. Detect Numbers: If the character is numeric, we build the current number.

    PYTHON
    1if ch.isnumeric():
2    num = num * 10 + int(ch)

  4. Handling Parentheses: When we encounter an open parenthesis, we push the current sign and parenthesis to the stack, and then reset sign to '+'.

    PYTHON
    1if ch == "(":
2    stack.append(sign)
3    stack.append('(')
4    sign = '+'

  5. Handle Operations and Close Parenthesis: When we encounter any operator or close parenthesis, we perform the respective operation.

    PYTHON
    1if ch in "+-*/)" or i == len(s) - 1:
2    if sign == "+":
3        stack.append(num)
4    elif sign == "-":
5        stack.append(-num)
6    elif sign == "*":
7        stack.append(stack.pop() * num)
8    elif sign == '/':
9        stack.append(int(stack.pop() / num))

  6. Close Parenthesis Logic: If we encounter a close parenthesis, we process the numbers within the parenthesis and sum them up.

    PYTHON
    1if ch == ')':
2    num, item = 0, stack.pop()
3    while item != '(':
4        num += item
5        item = stack.pop()
6    sign = stack.pop()

  7. Reset for Next Loop: Finally, we reset num and sign for the next iteration.

    PYTHON
    1else:
2    num = 0
3    sign = ch

  8. Sum it Up: At the end, our stack will contain the numbers we need to sum to get the answer.

    PYTHON
    1return sum(stack)

  9. Test the Function: We'll use an example to test our function.

    PYTHON
    1print(calculator("4*(3+2)"))  # Output should be 20
RUN CODERESET
CSHARP
OUTPUT
:001 > Cmd/Ctrl-Enter to run, Cmd/Ctrl-/ to comment

One Pager Cheat Sheet

  • Let's program a very basic calculator, handling positive, negative symbols, parentheses, and spaces, without using eval function!
  • In most languages, you can evaluate code strings quickly and easily using eval.
  • We can break down the problem into parsing and evaluating symbols such as integers, signs/operations, parenthesis and spaces, and iterate through an expression string to transform it into a form understandable by the machine, with some caveats in the processing order.
  • Adding a negative number to our running result is the key to solving the problem of subtraction.
  • We can keep track of our sign while converting the signs of numbers by using 1 or -1 to represent the + or - operations respectively.
  • Leveraging two stacks to keep track of the result and operations within the parentheses is the key to solving this challenging problem.
  • We skip that iteration if the current character is a space.
  • We can iterate through the input of length n in O(n) time and space complexity.
  • We can extend our previous solution to handle Multiplication and Division by using a stack to store multipliers and dividers and multiplying or dividing the result of each for loop iteration by this stack as it pops values off.
  • Byrecreatingthe parentheses expression on a stack, we can still use the left-to-right approach to parse"4*(3+2)", instead of being "drawn to the parentheses".

This is our final solution.

To visualize the solution and step through the below code, click Visualize the Solution on the right-side menu or the VISUALIZE button in Interactive Mode.

RUN CODERESET
CSHARP
OUTPUT
:001 > Cmd/Ctrl-Enter to run, Cmd/Ctrl-/ to comment

Great job getting through this. Let's move on.

If you had any problems with this tutorial, check out the main forum thread here.

Programming Categories

  • Basic Arrays Interview Questions
  • Binary Search Trees Interview Questions
  • Dynamic Programming Interview Questions
  • Easy Strings Interview Questions
  • Frontend Interview Questions
  • Graphs Interview Questions
  • Hard Arrays Interview Questions
  • Hard Strings Interview Questions
  • Hash Maps Interview Questions
  • Linked Lists Interview Questions
  • Medium Arrays Interview Questions
  • Queues Interview Questions
  • Recursion Interview Questions
  • Sorting Interview Questions
  • Stacks Interview Questions
  • Systems Design Interview Questions
  • Trees Interview Questions

    • Popular Lessons

  • All Courses, Lessons, and Challenges
  • Data Structures Cheat Sheet
  • Free Coding Videos
  • Bit Manipulation Interview Questions
  • Javascript Interview Questions
  • Python Interview Questions
  • Java Interview Questions
  • SQL Interview Questions
  • QA and Testing Interview Questions
  • Data Engineering Interview Questions
  • Data Science Interview Questions
  • Blockchain Interview Questions
  • Risk Management in C++
  • React Component Lifecycle
  • Advancing your Search Engine
  • Feature: Software Architectural Patterns & Design Structures
  • Linked Lists