Good evening! Here's our prompt for today.

Write a method to determine how deep a binary tree goes. The tree's depth can be described as the number of nodes you encounter as you traverse from the root node to a leaf.

The root node is the topmost node, and a leaf is a node with no children.

For example, you're given the following binary tree:

1    6
2   / \
3  2  14
4    /  \
5   13   19

The longest distance is from 6 to 19, and we return 3 because it covers 3 nodes.

The method will be invoked like the following:

1const root = new Node(6);
2
3function howDeep(root) {
4    return;
5};
6
7howDeep(root);

Constraints

• Number of nodes in the tree <= 100000
• The nodes will always contain integer values between -1000000000 and 1000000000
• Expected time complexity : O(logn)
• Expected space complexity : O(n) considering the call stack

Try to solve this here or in Interactive Mode.

How do I practice this challenge?

xxxxxxxxxx

  console.log('PASSED: ' + 'assert.deepEqual(howDeep(tree1), 2);');

var assert = require('assert');

​

function howDeep(root) {

  // Fill in this method

  return root;

}

​

function Node(val) {

  this.val = val;

  this.left = null;

  this.right = null;

}

​

// Regular binary trees

var tree1 = new Node(4);

tree1.left = new Node(1);

tree1.right = new Node(3);

​

var tree2 = new Node(5);

tree2.left = new Node(10);

tree2.left.left = new Node(17);

tree2.left.right = new Node(3);

tree2.right = new Node(8);

​

// Binary search trees

var tree3 = new Node(6);

tree3.left = new Node(3);

​

var tree4 = new Node(5);

Here's how we would solve this problem...

How do I use this guide?

This seems like a pretty straightforward problem: we essentially want to just count the maximum number of levels that the tree has. There's several ways to do this, but we'll need to traverse the tree.

Given that it's a binary tree, this means that there's up to two paths to move -- left and right. This fact simplifies things a bit, as traversal just requires navigating two children at each node.

During traversal, we can detect a leaf either when there is no left or right:

xxxxxxxxxx

if (!node.left && !node.right) {

  return;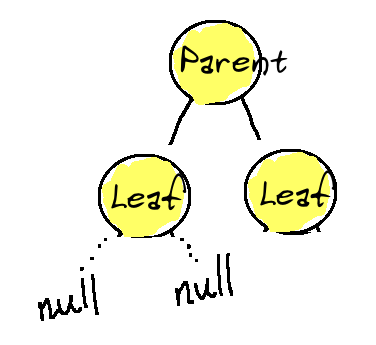

}

Or we could simply return when there is no node at all.

xxxxxxxxxx

if (!node) {

  // if parent returned twice here (left/right), it was a leaf

  return;

}

At every node, we can recursively traverse down the left and right children if they exist, until we reach a leaf.

The difficult part is keeping track of the number of levels.

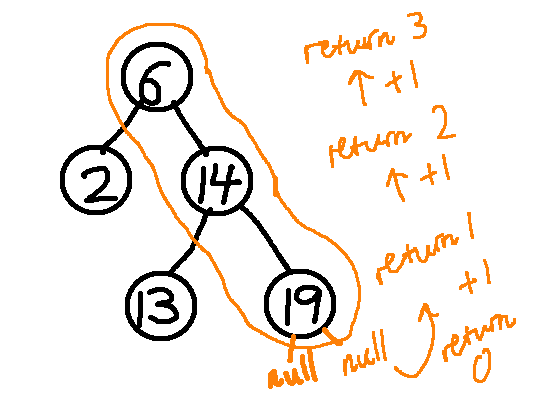
To do that, we can make the return statement the number of levels thus far, and increment it by 1 at every step.

This solution has a time complexity O(log n).