Good evening! Here's our prompt for today.

Given a binary tree representation, can you come up with a method to serialize the tree and then deserialize it to get the exact same tree?

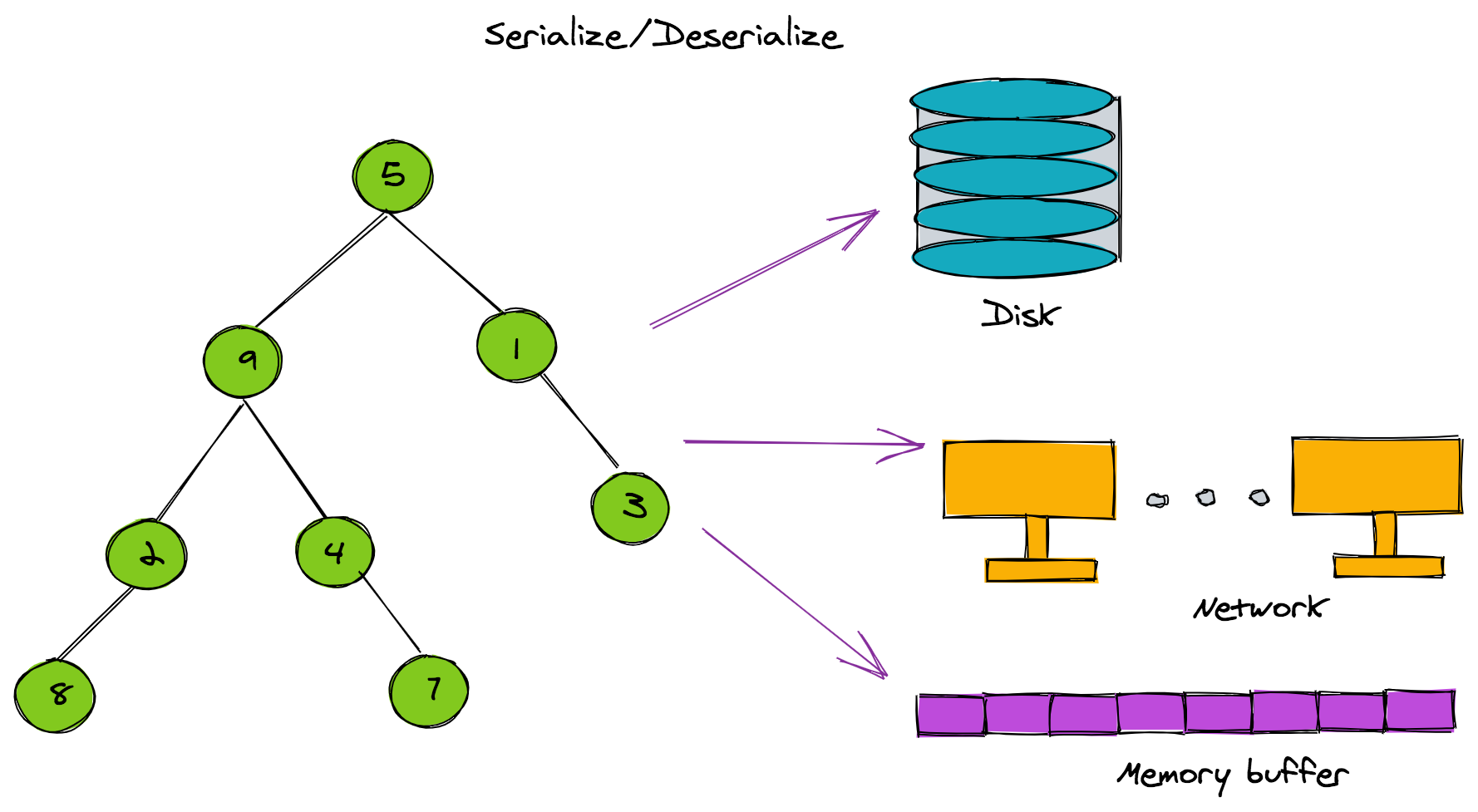
What is Serialization and Deserialization?

Serialization is a process that converts a data structure to a suitable format that can be stored either on a file or in memory. It can also be a format for data transmission across a network. Deserialization is the reverse process of recovering the original data structure. In this tutorial, I will show you how you can convert a binary tree with integer keys into an integer array and vice versa. You can then save the integer array in a text or binary file. You can also convert this integer array into a suitable format for data transmission over a network.

There are many ways of serializing a binary tree. Most of the methods involve traversing the tree, while storing each key in a data structure. Understanding a traversal is therefore the key to understanding the serialization and its reverse deserialization process. In this tutorial, we'll look at preorder traversal and how it can be used for serializing and deserializing a binary tree.

Try to solve this here or in Interactive Mode.

How do I practice this challenge?

xxxxxxxxxx

  assert.equal(serialized, '5 10 17 e e 3 e e 8 e e ');

var assert = require('assert');

​

function serialize(root) {

  // fill in this method

  return {};

}

​

function deserialize(data) {

  // fill in this method

  return {};

}

​

function Node(val) {

  this.val = val;

  this.left = null;

  this.right = null;

}

​

// Regular binary trees

var tree1 = new Node(4);

tree1.left = new Node(1);

tree1.right = new Node(3);

​

var tree2 = new Node(5);

tree2.left = new Node(10);

tree2.left.left = new Node(17);

tree2.left.right = new Node(3);

tree2.right = new Node(8);

​

Here's how we would solve this problem...

How do I use this guide?

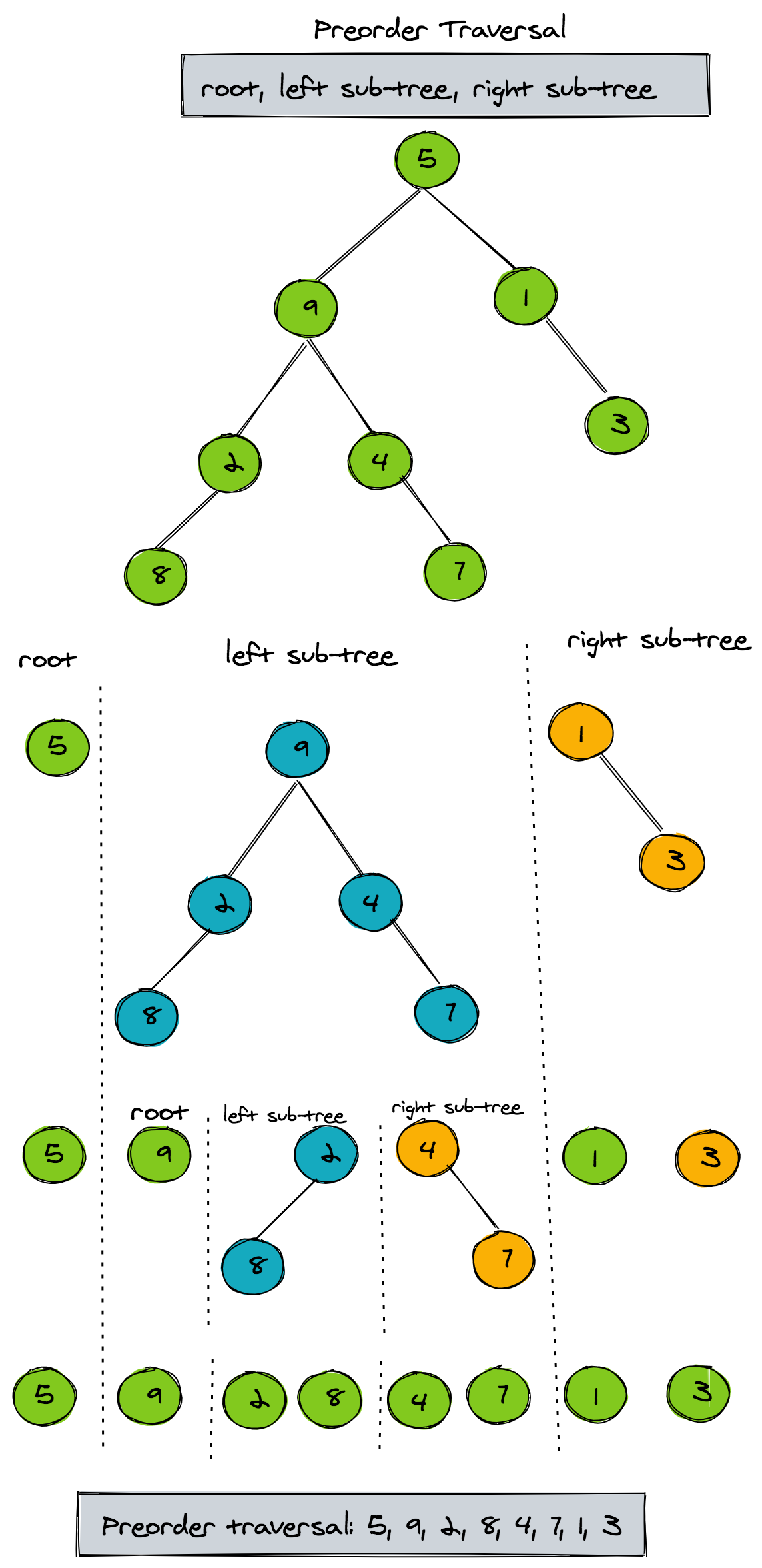
Preorder Traversal of a Binary Tree

There are many ways of traversing a tree, depth first or breadth first. For depth first traversal, the most popular methods are inorder, preorder and postorder traversal. The rule for preorder traversal is:

1Process root, process left sub-tree, process right sub-tree

What does this rule mean for a binary tree? The figure below shows the recursive preorder traversal of all keys in the binary tree.

Pseudo-code for Preorder Traversal

The simplest algorithm for preorder traversal exploits the recursive structure of a binary tree. The easiest method is to write a recursive preorder traversal routine as given here.

You can go back and look at the figure to see how the preorder recursive routine is working.

xxxxxxxxxx

Routine: preorder

Input: n = root node of tree

​

Base case: n is null

1. if n==null

    return

​

Recursive case:

1. display n

2. preorder(n.left)

3. preorder(n.right)

Serializing Using Preorder Traversal

We can modify the preorder routine to serialize a binary tree. All we need is a designated key to specify a null link. For this example, let's assume that we can only store zero or positive keys in the tree. Here, we can use -1 as a special key to denote a null link. The figure below shows the output array for the tree of our earlier example.

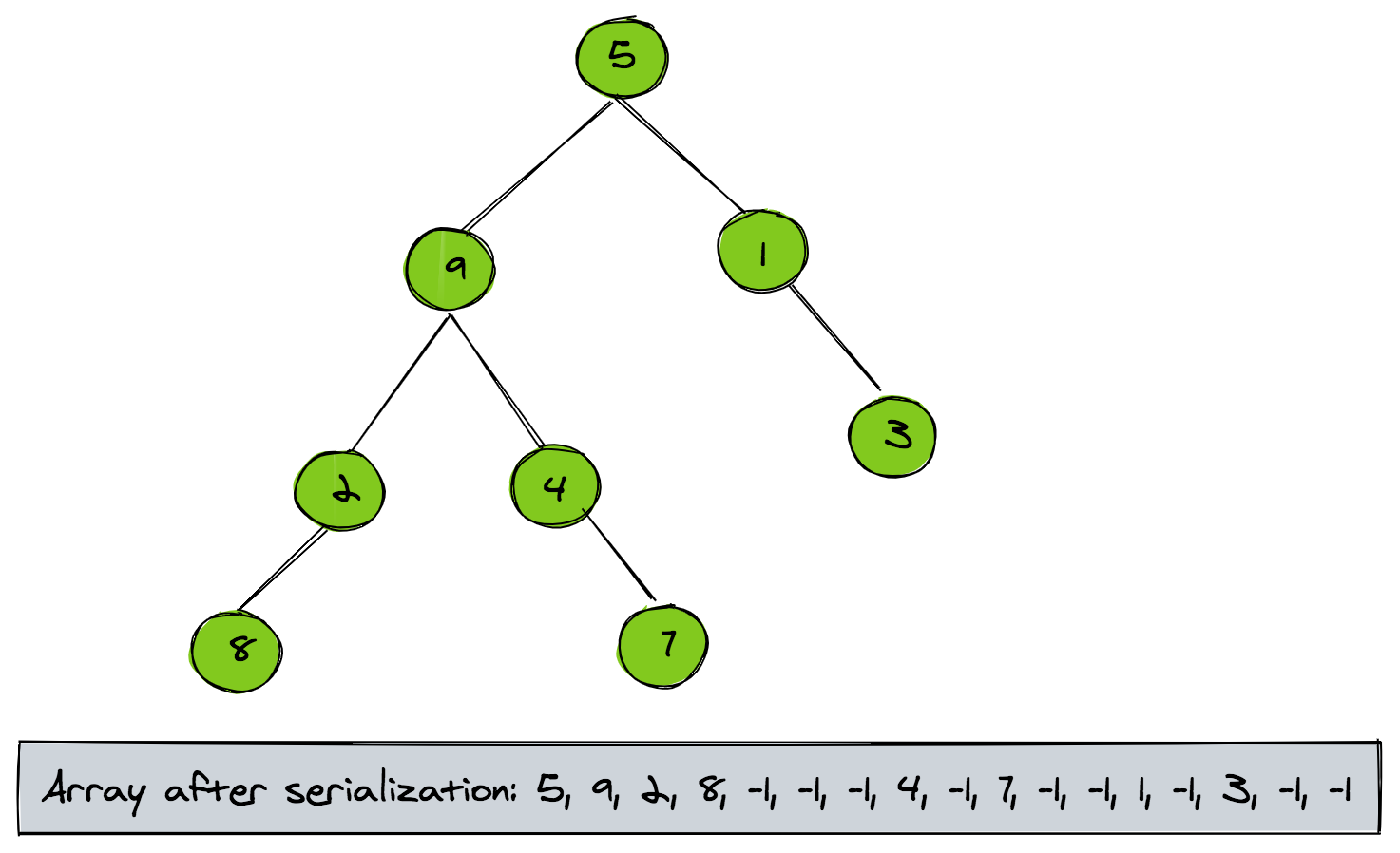
The pseudo-code for the serialization process is given below:

xxxxxxxxxx

Routine: treeToArray

Input: n = root of tree

Output: arrKeys: array of keys

​

Base case: n==null

1. arrKeys.add(-1)

​

Recursive case:

1. arrKeys.add(n.key);

2. treeToArray(n.left)

3. treeToArray(n.right)

Deserialization Using Preorder Traversal

If we serialize using preorder traversal, we have to apply the same preorder procedure to recursively build the tree. We'll take the keys from the array one by one and build the tree accordingly. The routine arrayToTree takes two arguments, i.e., the array of keys and an index. The base case would be true either when index passed is out of bound or if the key at index position is -1. Calling the routine with arrkeys and index = 0, would return the root node. The figure below illustrates how the tree is built.

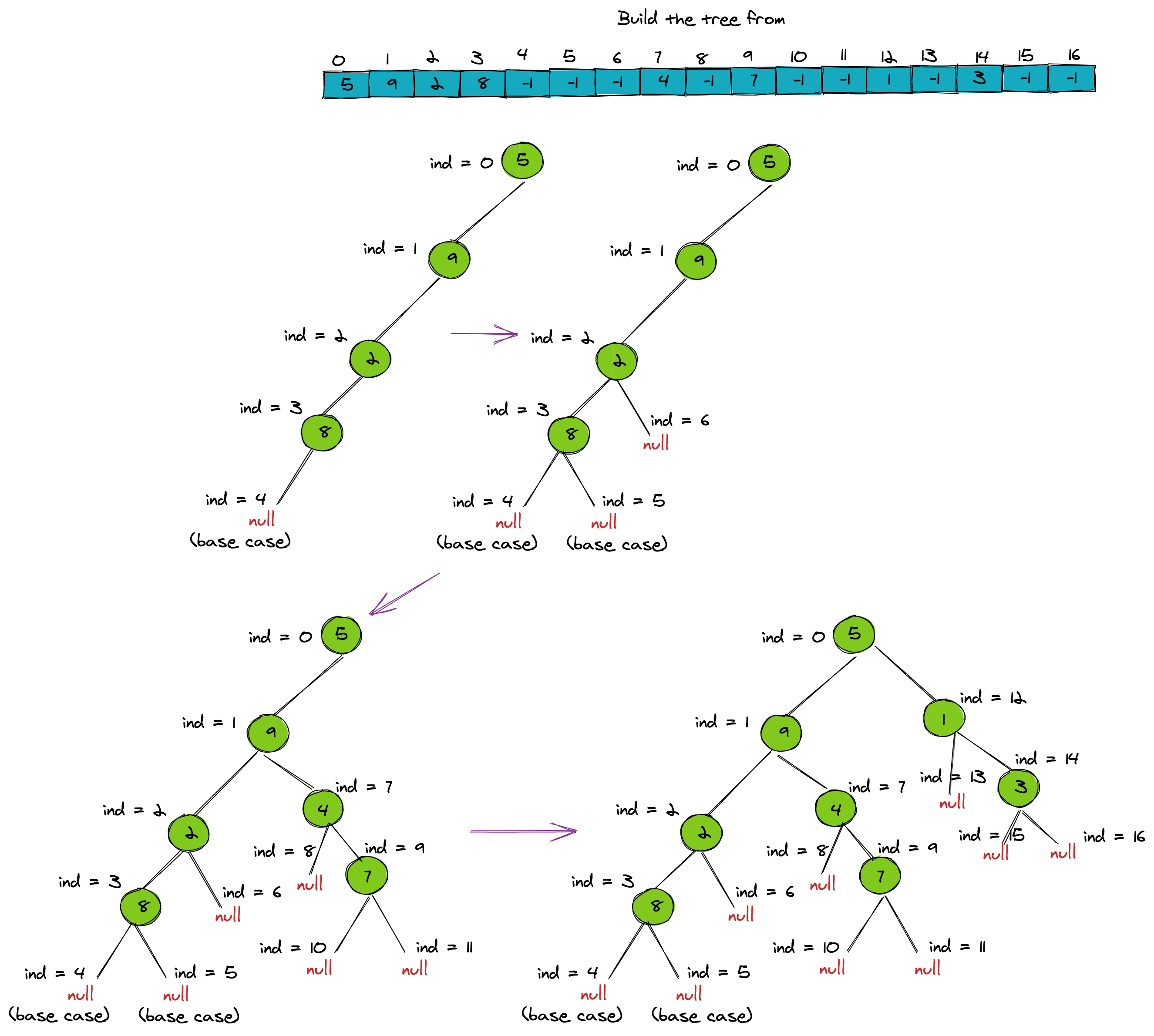
xxxxxxxxxx

Routine: arrayToTree

Input: arrKeys = array of keys, ind = index of array

Output: root node of binary tree

​

Base case 1: ind >= arrKeys.length

1. return null

​

Base case 2: arrKeys[ind] == -1

1. return null;

​

Recursive case:

1. n = create a new node with key = arrKeys[ind]

2. ind = ind+1;

3. n.left = arrayToTree(arrKeys,ind);

4. ind = ind+1;

5. n.right = arrayToTree(arrKeys,ind);

6. return n;

Java Code for Serialization and Deserialization

The Java code for both serialization (treeToArray method) and deserialization (arrayToTree method) is given below. For the treeToArray method, I have used an ArrayList object to add keys to the list. ArrayList is a convenient data structure to use if we don't know the size of the array in advance.

Note that for all the recursive routines, we need a public function to be called from outside the class and a corresponding helper function.

Wrapping it up

I hope you enjoyed working on this problem. Note, preorder traversal is not the only method of serialization. You can use methods based on inorder or postorder traversal. You can also use a level order traversal if you wish. Do try this out for different trees and see how the recursion is working. If n is the number of keys in the tree, then both serialization and deserialization have a complexity of O(n), as each key is traversed only once. Also, the array for storing the binary tree requires O(n) space as all keys in addition of null links are stored. Even if the links are double the size of total keys, the space complexity remains O(n).

xxxxxxxxxx

}

import java.util. * ;

import java.lang. * ;

//binary tree class

class node {

  int key;

  node left;

  node right;

  public node(int k) {

    key = k;

  }

  public void setLeft(int x) {

    left = new node(x);

  }

  public void setRight(int x) {

    right = new node(x);

  }

​

}

​

class binaryTree {

  node root;

  int ind;

​

  public int[] treeToArray() {

    //we'll create an array list and then convert it to array

    //as we don't know in advance how many keys have to be stored

    ArrayList < Integer > arrList = new ArrayList < Integer > ();

    //call helper that recursively adds to array

    treeToArray(root, arrList);