Good afternoon! Here's our prompt for today.

We are given a binary tree and are tasked with writing a method that determines the average of every level in the tree. So for instance, given the following binary tree, we'd get [2, 5, 7] if the method grabbed the correct means.

1/*
2       2
3      / \
4     3   7
5    / \   \  
6   4   8   9 
7*/
8
9meanOfLevels(root);
10// [2, 5, 7]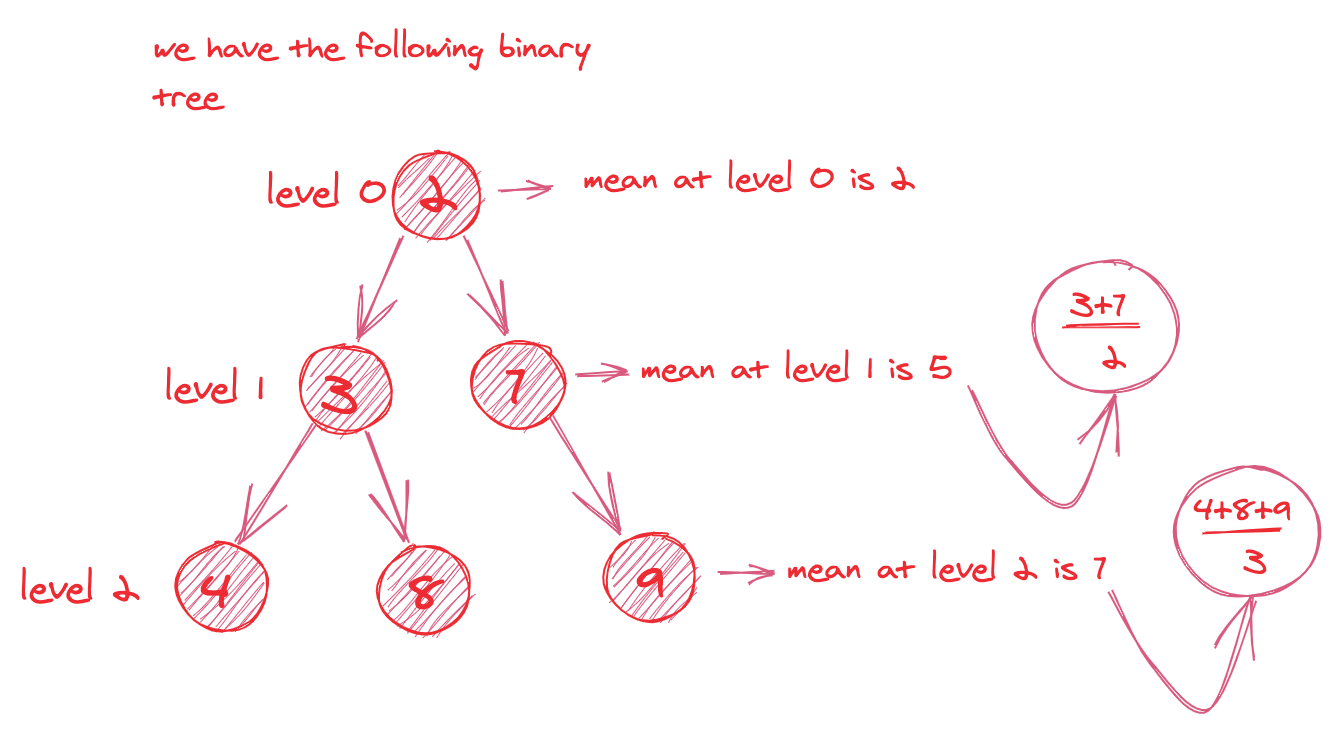

You may assume the standard tree node definition of:

1function Node(val) {
2  this.val = val;
3  this.left = this.right = null;
4}
5
6const root = new Node(2);
7root.left = new Node(3);
8root.right = new Node(7);
9root.left.left = new Node(4);
10root.left.right = new Node(8);
11root.right.right = new Node(9);
12console.log(meanOfLevels(root));

Constraints

• The nodes will always contain integer values between -1000000000 and 1000000000
• In case the division is not proper, add the quotient to the list and ignore the remainder
• You may assume that while adding the numbers, the sum will not overflow the integer range
• Expected time and space complexity : O(n) for both
• In case the tree is null, return an empty list

Try to solve this here or in Interactive Mode.

How do I practice this challenge?

xxxxxxxxxx

  console.log('PASSED: ' + 'assert.deepEqual(meanOfLevels(tree3), [6, 3]);');

var assert = require('assert');

​

function meanOfLevels(head) {

  return head;

}

​

function Node(val) {

  this.val = val;

  this.left = null;

  this.right = null;

}

​

// Regular binary trees

var tree1 = new Node(4);

tree1.left = new Node(1);

tree1.right = new Node(3);

​

var tree2 = new Node(5);

tree2.left = new Node(10);

tree2.left.left = new Node(17);

tree2.left.right = new Node(3);

tree2.right = new Node(8);

​

// Binary search trees

var tree3 = new Node(6);

tree3.left = new Node(3);

​

var tree4 = new Node(5);

tree4.left = new Node(3);

Here's our guided, illustrated walk-through.

How do I use this guide?