AlgoDaily - Implement a Hash Map

Good evening! Here's our prompt for today.

Arrays are amazing for looking up elements at specific indices as all elements in memory are contiguous, allowing for O(1) or constant time lookups. But often we don't, or can't, perform lookups via indices. Hash maps and hash tables are a way around this, enabling us to lookup via keys instead.

Can you implement the Map class from scratch? Only two methods are necessary-- get and set. Many programming languages have a built-in hash or dictionary primitive (like Javascript Objects and {} notation), but we don't want to use that for this exercise.

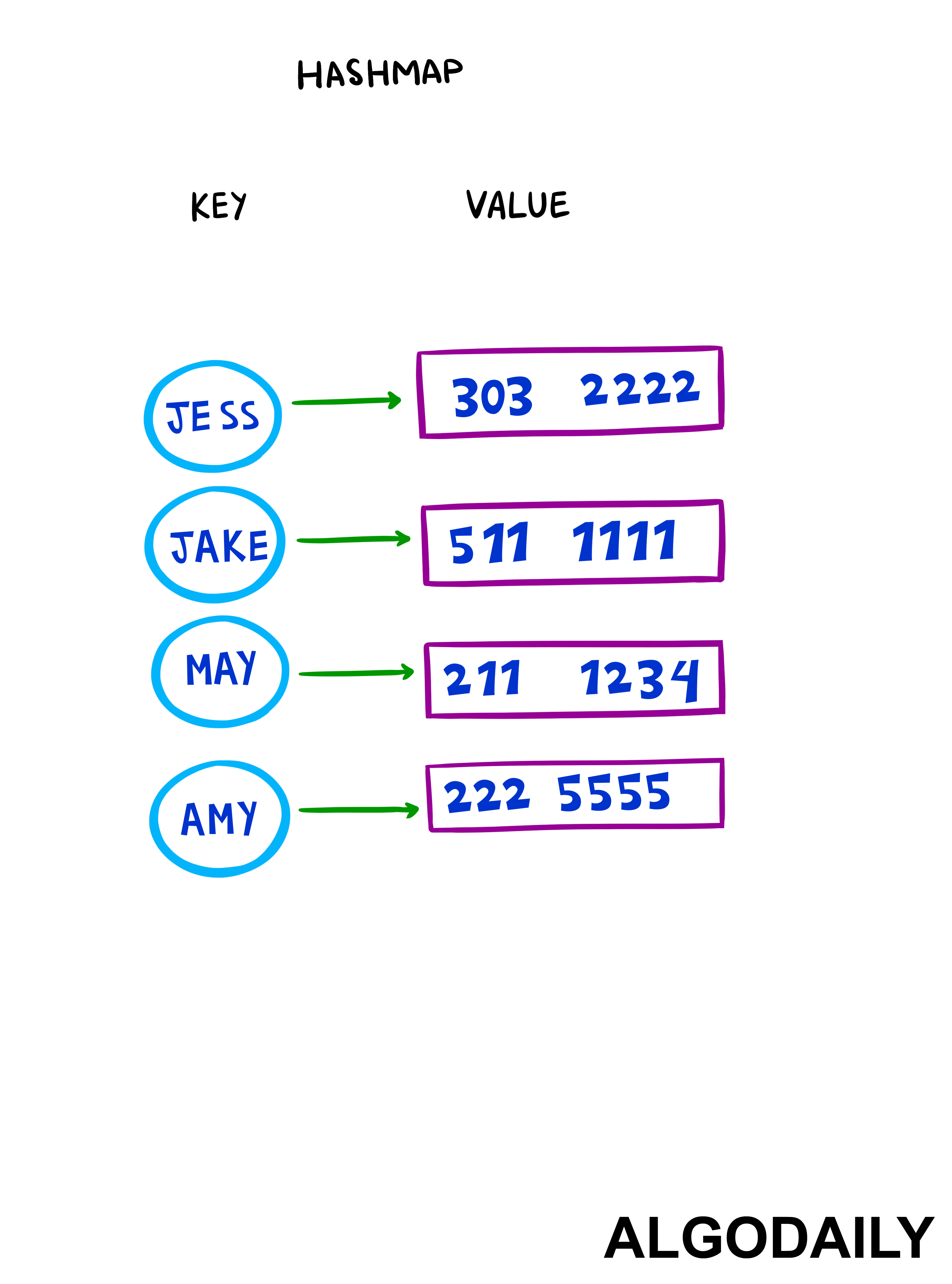
Note: Regular Javascript objects and the Map class are both simple key-value hash tables/associative arrays, with a few key differences:

A Map object can iterate through its elements in insertion order, whereas JavaScript's Objects don't guarantee order. In addition, Objects have default keys due to their prototype, and Maps don't come with default keys. Here's a good breakdown of the two. For the purpose of this exercise, let's assume the same functionality for both.

For the two methods you'll define:

get(key: string) should be given a key, and return the value for that key.
set(key: string, val: string) should take a key and a value as parameters, and store the pair.

Additionally, we've supplied the below hashing function hashStr. It tries to avoid collision, but is not perfect. It takes in a string value and returns an integer.

1public class Main {
2  public static int hashStr(String str) {
3    int finalHash = 0;
4    for (int i = 0; i < str.length(); i++) {
5      char charCode = str.charAt(i);
6      finalHash += (int) charCode;
7    }
8    return finalHash;
9  }
10
11  public static void main(String[] args) {
12    System.out.println(hashStr("testKey"));
13  }
14}

Let's call our new class the Hashmap class, and use it like such:

1import java.util.HashMap;
2
3public class Main {
4  public static void main(String[] args) {
5    HashMap<String, String> m = new HashMap<>();
6    m.put("name", "Jake");
7    System.out.println(m.get("name"));
8  }
9}

Constraints

Sum of lengths of the string <= 10000
The string will consist of ASCII characters
Expected time complexity for inserting a key,value pair and retrieving a value : O(1)
Expected space complexity : O(n)

Try to solve this here or in Interactive Mode.

How do I practice this challenge?

xxxxxxxxxx
​
 
import org.junit.Test;
import org.junit.runner.JUnitCore;
import org.junit.runner.Result;
import org.junit.runner.notification.Failure;
​
import static org.junit.Assert.*;
​
// solution
​
class Hashmap {
​
    // fill in
    // with solution
​
    public Hashmap() {
        // fill in
        // with solution
    }
​
    public void set(String key, Object val) {
        // fill in
        // with solution
    }
​
    public Object get(String key) {
        // fill in
        // with solution
        return null;
    }

Tired of reading? Watch this video explanation!

To change the speed of the video or see it in full screen, click the icons to the right of the progress bar.

Here's our guided, illustrated walk-through.

How do I use this guide?

Let's begin by revisiting how a general hash table works, the theory being what our Hashmap data structure will be based off. As we've noted, in many programming languages, there is a Hashmap class that's based off a legacy Hashtable. Let's step through our suggested implementation of this code.

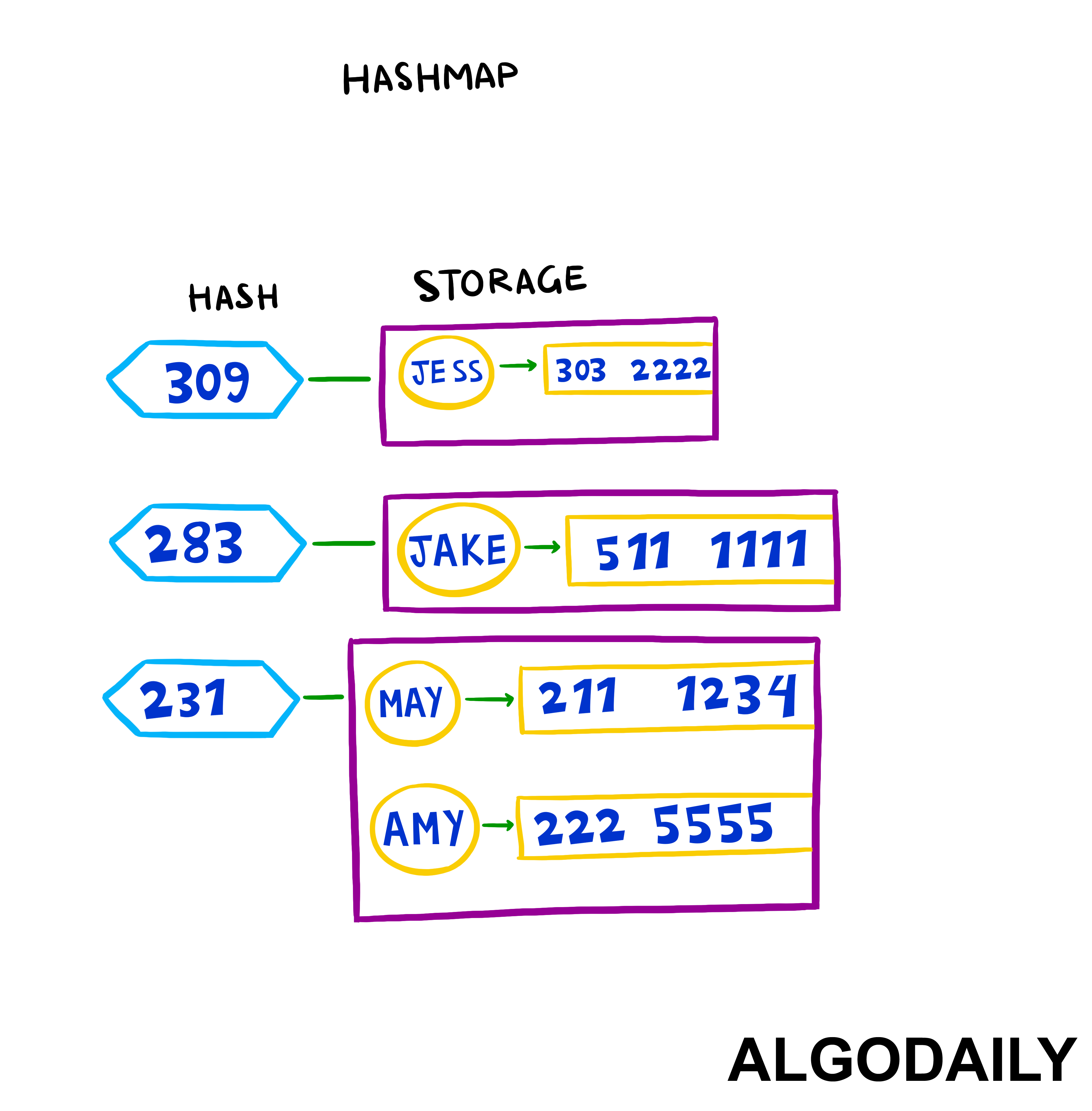
So we know that hash tables work by storing data in buckets. To access those buckets, we'll need a way to convert a key to an bucket number. (The buckets can be modeled using both arrays and binary search trees, but to keep things simple and maximize speed, we'll stick with using arrays.)

Using keys decouples us from having to know where the data is in the array. Our data structure thus needs a hash function, provided in this case as hashStr, to calculate an index into buckets where the wanted value is stored. We're essentially mapping the key to an array index via our hashStr hash function.

SNIPPET

1hashStr('r')
2// 114
3
4// array = [  _  ,  X  ,  _  ,  _ ]
5// index     113   114   115   116

As you can see, all hashStr does is take the key provided in set(), and computes a location for us. We'll thus need another data structure for the actual storage and buckets that the values are placed. Of course, you already know it's an array!

Let's test your knowledge. Fill in the missing part by typing it in.

The slots or buckets of a hash table are usually stored in an ___ and its indices.

Write the missing line below.

A good start to writing the class is to initialize it with just the bare minimums. We need a storage array, so let's start there:

1public class Hashmap {
2  private Object[] _storage;
3
4  public Hashmap() {
5    this._storage = new Object[];
6  }
7}

We'll use the returned index of hashStr to decide where the entered value should go in this._storage.

A word on a collisions: collisions are when a hash function returns the same index for more than one key and are out of the scope of this question. However, there are ways to handle such issues using additional data structures.

Build your intuition. Click the correct answer from the options.

Which of the following is a solution for collisions in a hash table implementation?

Click the option that best answers the question.

There is no good solution for collisions, the hash function must be unique
Use separate chaining, often with a linked list, where the index of the array consists of a chain of values
Use a trie to store values at every index
Concatenate all the values as one single string at that bucket

At this point, we have our building blocks, so let's go ahead and implement the set method. The method will:

take the key passed
run it through the hash function, and
set the value in our storage at that particular index

Notice the way we're storing it as well: each index in this._storage (this._storage[idx]) is itself an array, thereby primitively solving for the collision problem.

1public void set(String key, Object val) {
2  int idx = hashStr(key);
3
4  if (this._storage[idx] == null) {
5    this._storage[idx] = new ArrayList<>();
6  }
7
8  this._storage[idx].add(new Object[] {key, val});
9}

The set method now seems pretty straightforward, right?

It's the same concept with our get method. What we're doing there is also running the passed key through the hashStr method, but instead of setting, we'll go to the resulting index and retrieve/return the found value.

1for (Object[] keyVal : this._storage[idx]) {
2  if (keyVal[0].equals(key)) {
3    return keyVal[1];
4  }
5}

One caveat we should note is that it's possible to pass a key that doesn't exist (or has not been set), so we should handle that by returning undefined or None if that's the case.

1public Object get(String key) {
2  int idx = hashStr(key);
3
4  if (this._storage[idx] == null) {
5    return null;
6  }
7
8  for (Object[] keyVal : this._storage[idx]) {
9    if (keyVal[0].equals(key)) {
10      return keyVal[1];
11    }
12  }
13}

That should about do it! Let's try it out.

Complexity for Final Solution

The hash map data structure grows linearly to hold n elements for O(n) linear space complexity. Assuming a good hash function (one that minimizes collisions!) we usually have O(1) constant get/set complexity. Otherwise, in the worst case where all n entries hash to the same bucket we traverse through for an unfortunate O(n) linear get/set complexity.

One Pager Cheat Sheet

You can implement a Hashmap class from scratch, with the get and set methods for retrieving and storing key and value pairs, and a hashing function for converting strings to integers, to enable O(1) lookups.
We are creating a Hashmap data structure based off a legacy Hashtable, taking advantage of a hash function to map keys to buckets and store our data in the corresponding index of an array.
The key provided to set() is used to compute a location in the hashStr() function, and an array is needed for the actual value storage.
The slots of a hash table are typically stored in an array whose indices refer to the computed location given by the hash function, and whose buckets refer to the data structure in which the key-value pairs are stored for efficient insertion and retrieval.
Creating a class with a storage array as the bare minimum is a good initialization step.
We will hashStr to determine the appropriate index to store the value in this._storage, and handle any possible collisions using additional data structures.
Hash tables can use a linked list structure to store multiple values at the same index to prevent collisions.
We can implement the set method by converting the key to an index in this._storage and setting the value using an array to primitively solve for the collision problem.
Both get and set methods take a key as an argument and use the hashStr method to find the appropriate index in a data structure; get returns the value located at the index, while set stores a key-value pair at the indexed location.
When using these methods, we should always check to see if a key exists and handle any cases where it doesn't by returning undefined or None.
The hash map data structure grows linearly with O(n) space complexity, with O(1) constant get/set complexity in most cases, and O(n) linear get/set complexity in the worst case.

This is our final solution.

To visualize the solution and step through the below code, click Visualize the Solution on the right-side menu or the VISUALIZE button in Interactive Mode.

xxxxxxxxxx
}
 
import org.junit.Test;
import org.junit.runner.JUnitCore;
import org.junit.runner.Result;
import org.junit.runner.notification.Failure;
​
import static org.junit.Assert.*;
​
import java.util.ArrayList;
​
class Hashmap {
​
    static class Entry {
        public final String key;
        public Object val;
​
        public Entry(String key, Object val) {
            this.key = key;
            this.val = val;
        }
    }
​
    private ArrayList<Entry>[] _storage;
​
    public Hashmap() {
        this._storage = new ArrayList[16];
    }
​
    public void set(String key, Object val) {
        int idx = hashStr(key) % 16;
​
        if (this._storage[idx] == null) {
            this._storage[idx] = new ArrayList<Entry>();

That's all we've got! Let's move on to the next tutorial.

If you had any problems with this tutorial, check out the main forum thread here.