Good morning! Here's our prompt for today.

Here's a fun one: let's say we have a 2D array matrix that is a size of m rows and n columns. It is initially prefilled with 0s and looks like the following:

1[[0, 0, 0, 0],
2 [0, 0, 0, 0],
3 [0, 0, 0, 0]]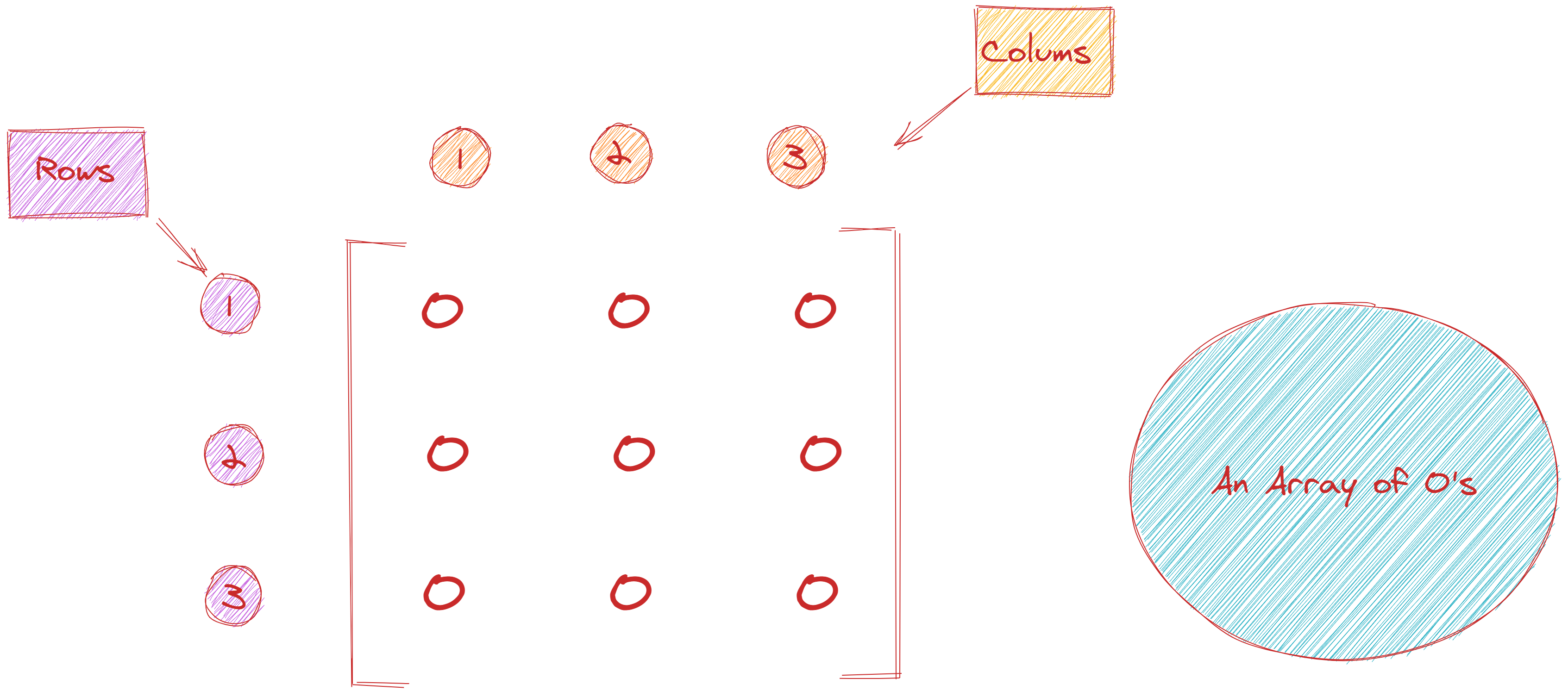

We are then given a list of increment operations to be performed on the nested matrix array. An increment operation is exactly as it sounds-- it will dictate when to add 1 to a number in the matrix.

Each increment operation will consist of two numbers, a row and column value, that dictate to what extent the array's cells under that range should increment by 1.

For example, given the above matrix, if we get [1, 1] as an operation, it results in:

1[[1, 0, 0, 0],
2 [0, 0, 0, 0],
3 [0, 0, 0, 0]]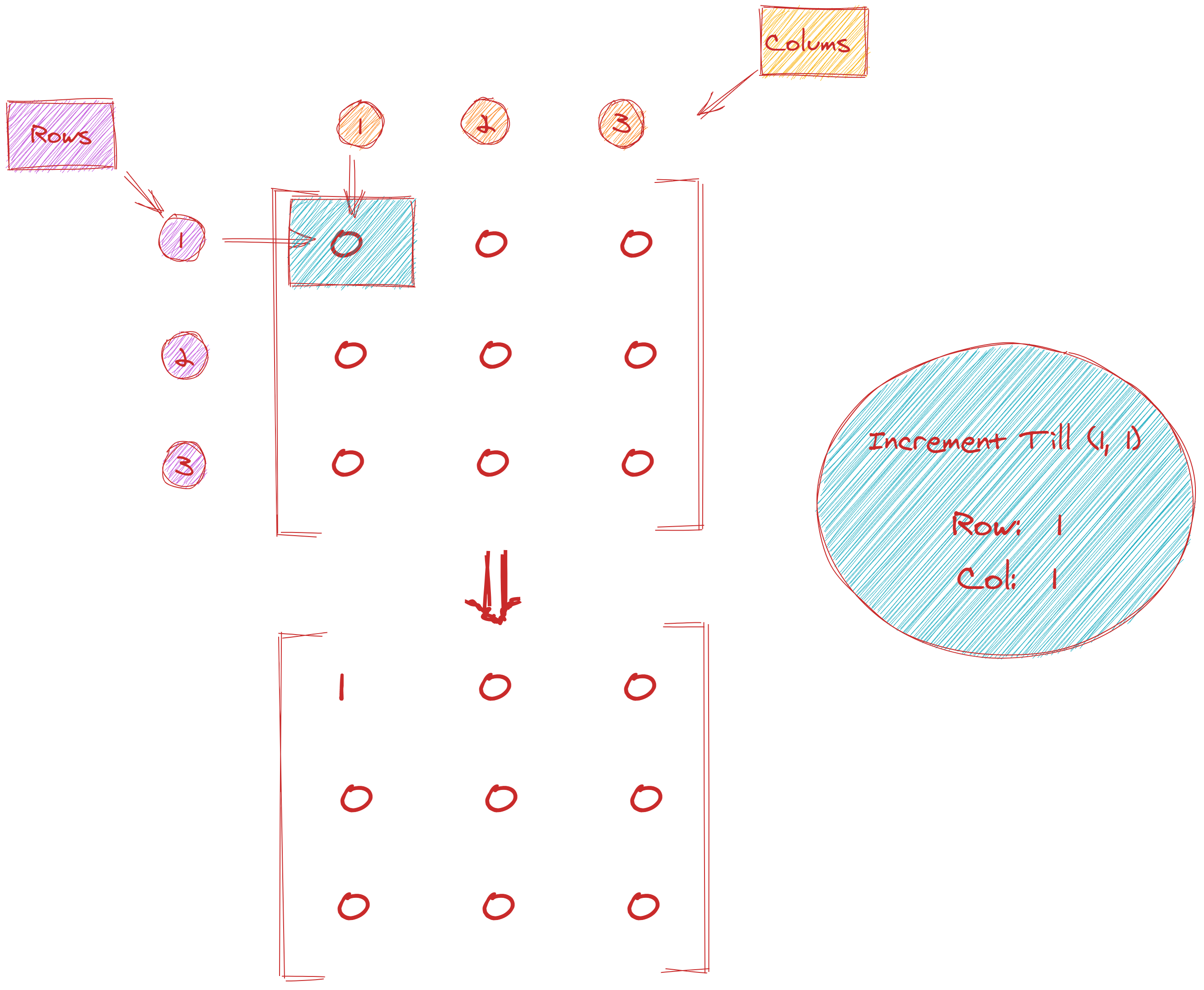

This is because we look at matrix[1][1], and look northwest to see what the "range" is. So what we've done is incremented all cells from matrix[0][0] to matrix[row][col] where 0 <= row < m, and 0 <= column < n.

If we then got another operation in the form of [2, 2], we'd get:

1[[2, 1, 0, 0],
2 [1, 1, 0, 0],
3 [0, 0, 0, 0]]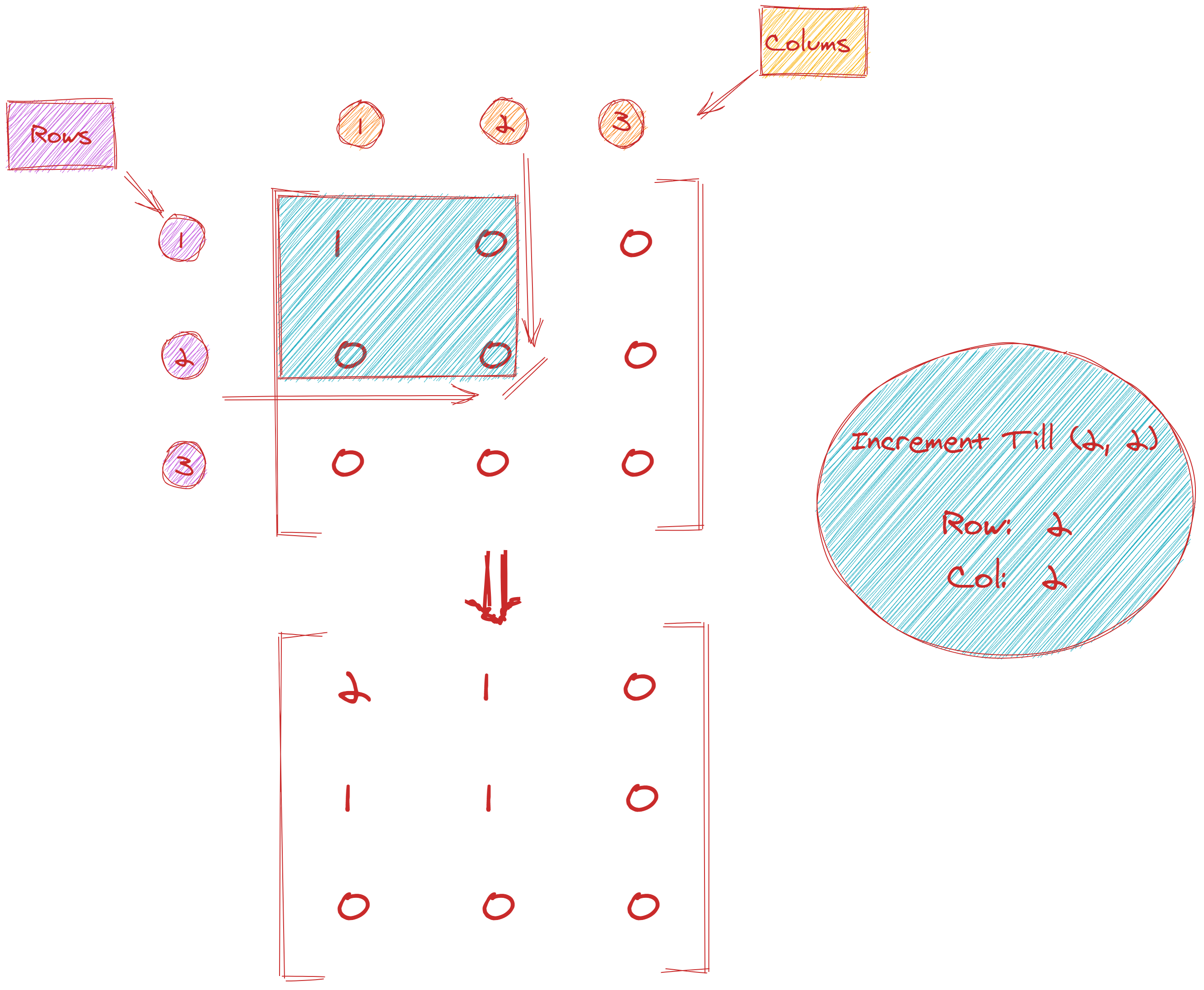

Can you write a method that returns the frequency of the max integer in the matrix? In the above example, it would be 1 (since 2 shows up just once).

Constraints

• Length of the array operations would be <= 100000
• The values of n and m <= 10000
• The values in operations will be in the range 1 and 10000
• Expected time complexity : O(n)
• Expected space complexity : O(1)

Try to solve this here or in Interactive Mode.

How do I practice this challenge?

xxxxxxxxxx

var assert = require('assert');

​

function maxFromOps(m, n, operations) {

  // fill this out

  return operations;

}

​

console.log(

  maxFromOps(4, 4, [

    [1, 1],

    [2, 2],

  ])

);

​

try {

  assert.equal(

    maxFromOps(4, 4, [

      [1, 1],

      [2, 2],

    ]),

    1

  );

​

  console.log(

    'PASSED: ' + 'Expect `maxFromOps(4, 4, [[1, 1], [2, 2]])` to return `1`'

  );

} catch (err) {

  console.log(err);

}

Here's how we would solve this problem...

How do I use this guide?

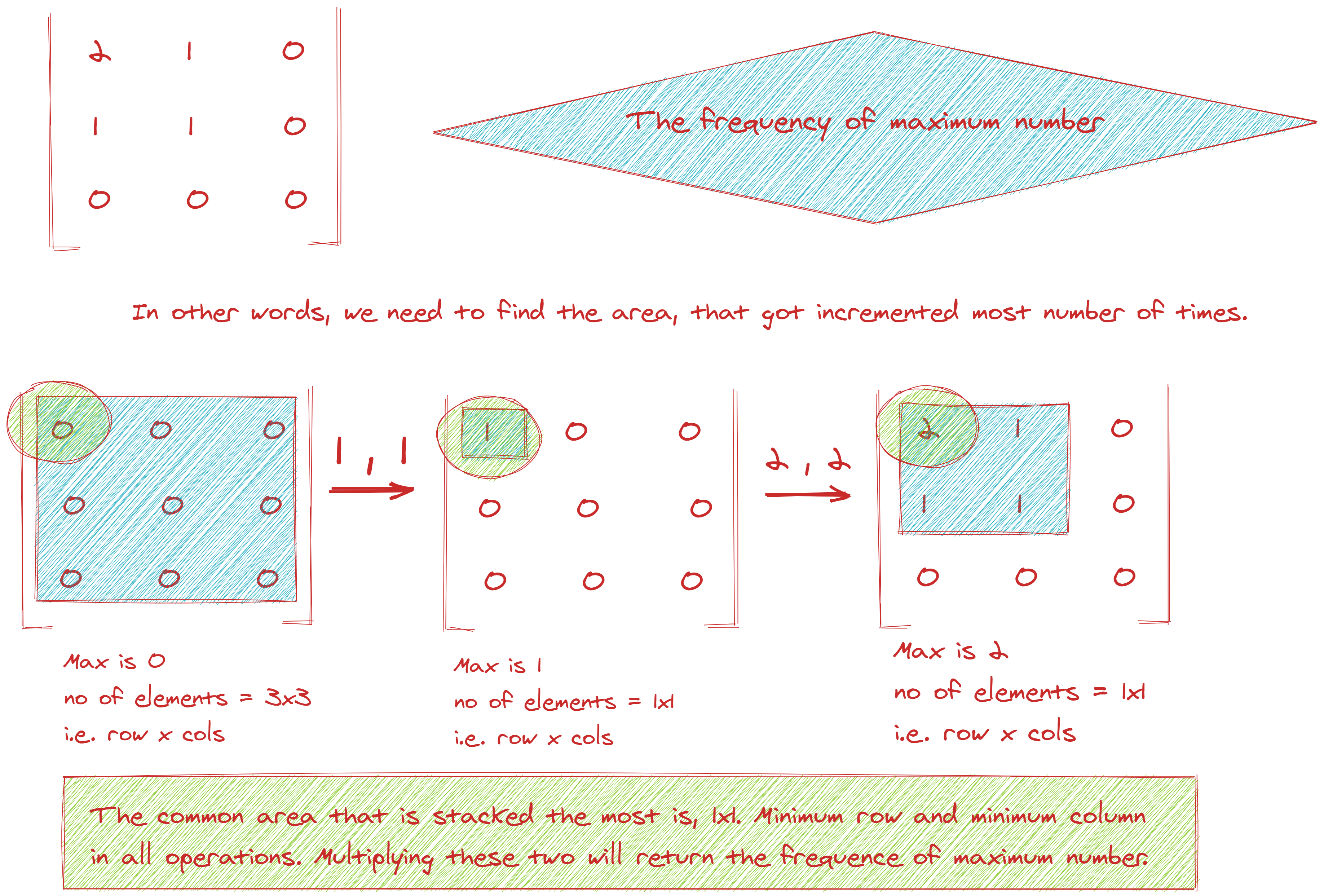
So let's analyze the example given. Starting from a blank state of all 0s, if we are given the operations [1, 1] and then [2, 2], we obtain:

xxxxxxxxxx

[[2, 1, 0, 0],

 [1, 1, 0, 0],

 [0, 0, 0, 0]]

The largest number is 2, and it's in the upper left. It got there because matrix[0][0] was incremented by 1 in both the operations.

Let's take a step back: so how do numbers in the matrix increment? It's via the overlap of the operations! What do we mean by this? The first operation gave us:

xxxxxxxxxx

[[1, 0, 0, 0],

 [0, 0, 0, 0],

 [0, 0, 0, 0]]

matrix[0][0] is now a 1. It gets bumped up again since it falls under the [2, 2] range. We can imagine the operations as layering over each other.

There is an associated insight from this one: the cells that are layered over the most are the ones with the greatest numbers.

So really the cells we're looking for are the ones that got layered over the most.

The easiest way to do is by looking at the minimum rows and columns of each operation, since those are the edges of coverage. The minimum guarantees that the greatest increments will at at least reach those boundaries.

Time and space complexity is O(n).