AlgoDaily - The Coin Change Problem

Good evening! Here's our prompt for today.

If I give you coins of denominations {3, 7, 9} (a coin worth 3 cents, a coin worth 7 cents, etc.), can you tell me the minimum number of coins that are needed to make a total of 37? You can assume that an infinite supply of all these coins are available to you.

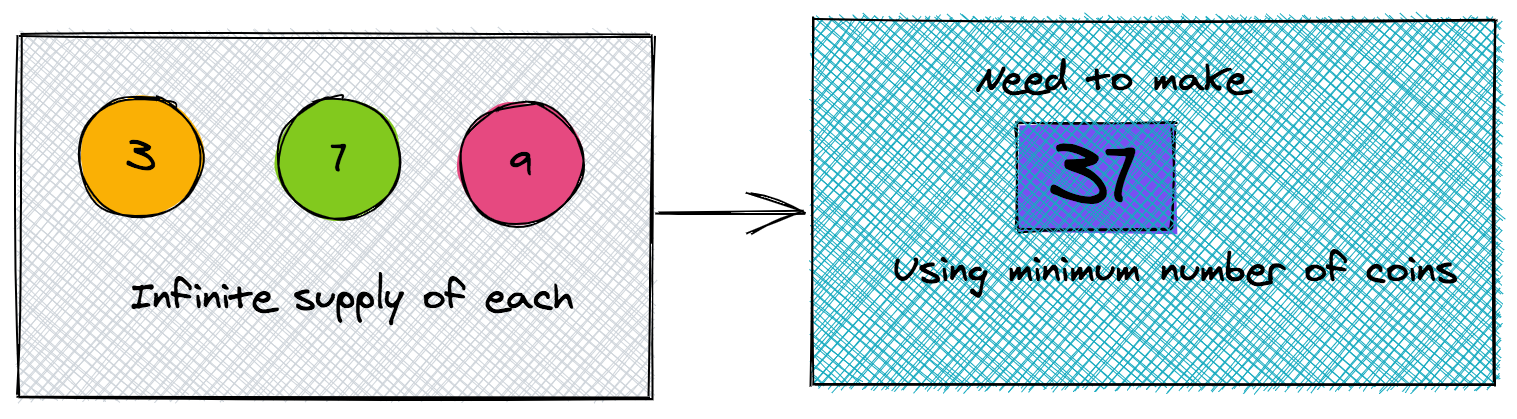
This challenge is about solving the change making problem using dynamic programming. The task is to find the minimum number of coins that add up to a given denomination amount. We are given a set (via an array) of coins of different denominations and assume that each one of them has an infinite supply.

Examples

Here are a few examples of the given inputs and the expected output. Note, for all these examples other combinations are also possible. We are only interested in the minimum number of coins, regardless of the combination of coins.

SNIPPET

11. coins = {2,3,5}      amount = 11:     use 3 coins, e.g., [3,3,5]
22. coins = {2,3,5,7}    amount = 17:     use 3 coins, e.g., [3,7,7]
33. coins = {2,3,7}      amount = 15:     use 4 coins, e.g., [2,3,3,7]
44. coins = {3,5}        amount = 7:      Not possible (inf)
55. coins = {2,3,5}      amount = 1:      Not possible (inf)

For the combinations that are not possible, it is a convention to use infinity to represent such a solution.

Constraints

Length of array coins <= 1000
Each denomination will be a non zero positive integer
Amount will be a non zero value and <= 1000
Expected time complexity : O(n^2)
Expected space complexity : O(n)

Try to solve this here or in Interactive Mode.

How do I practice this challenge?

xxxxxxxxxx
 
var assert = require('assert');
​
function coinChange(coins, amount) {
  // Fill in this method
  return 1;
}
​
try {
  assert.equal(coinChange([2, 3, 5], 11), 3);
​
  console.log('PASSED: ' + 'First Test: coinChange([2, 3, 5], 11)');
} catch (err) {
  console.log(err);
}
​
try {
  assert.equal(coinChange([2, 3, 5, 7], 17), 3);
​
  console.log('PASSED: ' + 'Second Test: coinChange([2, 3, 5, 7]');
} catch (err) {
  console.log(err);
}
​
try {
  assert.equal(coinChange([2, 3, 7], 15), 4);
​
  console.log('PASSED: ' + 'Third Test: coinChange([2, 3, 7], 15)');
} catch (err) {
  console.log(err);

We'll now take you through what you need to know.

How do I use this guide?

How to Solve the Coin Change Problem

This problem can be solved recursively. The idea behind the recursive solution is to try out all possible combinations that add up to amount, and pick the solution with a minimum number of coins. You might think that trying out all possible combinations means that we are opting for an exponential time complexity solution-- not the case!

Exponential time complexity problems aren't useful in real life, as the run-time will often kill the application. What we can do instead is to try out all possible combinations intelligently using dynamic programming. Dynamic programming will drastically cut down our search time for finding the solution.

Let me illustrate the idea behind the search for the solution using a simple example. Suppose we are given the coins [2, 3, 5] and amount = 11. Let's now look at the figure that shows us the solution:

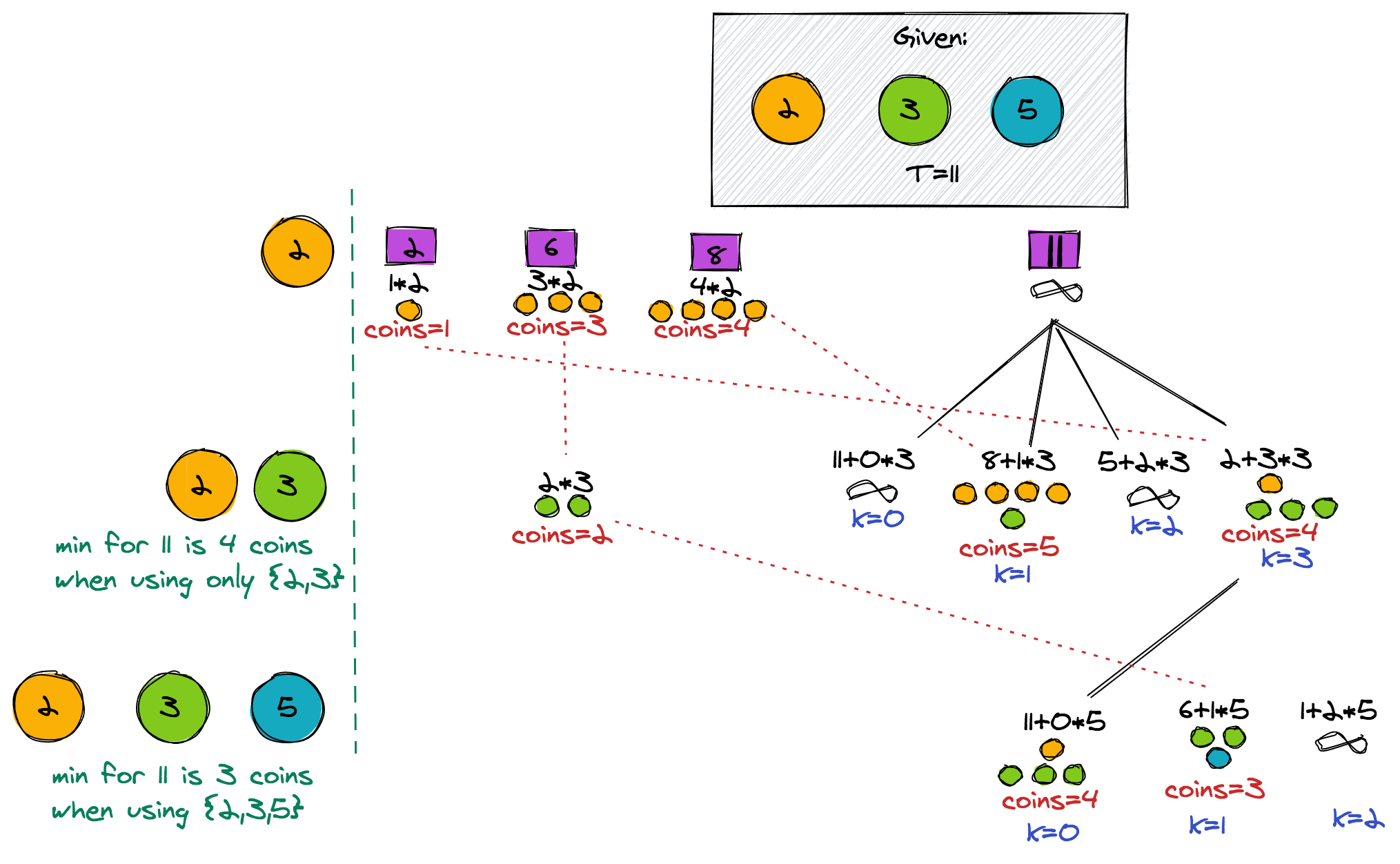
The idea here is to build a tree by making combinations with only coin {2} (level 1 of the tree). Then, we can make use of this information to make all combinations with {2, 3} (the second level of the tree). Finally, we'll all combinations with {2, 3, 5} in the third level. Notice that we cannot make 11 with just {2}, so we have infinity as the answer.

Going down one level, we make various combinations of 11 by adding the coin 3 in 4 ways (for example, we can add up {}, {3}, {3, 3}, or {3, 3, 3}. For these four branches, information from the previous level is required. For example, when no coin 3s are added, we need to know the optimal way to make 11 from just coin 2. When only one coin 3 is added (from, say, {3}), then we need to know the optimal way to make 8 from just coin 2. When {3, 3} is added, we need to know the optimal way to make 5 from just coin 2. The same is the case with {3, 3, 3}. For this level, pick the minimum number of coins (i.e. 4), with the combination {2, 3, 3, 3}.

This same idea is repeated with {2, 3, 5}. We can make 11 by adding coin 5 zero times, one time, or two times-- and pick the minimum from this list. We have as many "levels" as the number of coins. We also need to know the optimal way of making denominations for 1..amount. In this example, you can see that we needed denominations 2, 6, 8 starting at the first level of the tree. It is important to note that only the optimal number of coins has to be stored for each level.

Pseudo-Code for Coin Change

To implement the coin change problem, we'll resort to dynamic programming. The big idea is to solve smaller sub-problems and store their results to be used later. For example, in the previous example, we solved the smaller sub-problem for denomination 2, 6, 8 by using just coin {2}. Let's think about our solution:

There are as many levels in the tree as the number of coins
We need the solution for denominations (1 .. amount)
The next level requires the solution from the previous level

The best thing to do is to define an array matrix M, that stores the intermediate results. The size of the matrix is then N * (amount+1), whereN=number of unique coins and amount=denomination.

We have (amount+1) for simplicity so that an index value denotes a denomination and as the indices start from zero, we need (amount+1) columns. Initially, we set only the cells of M, whose column index is an integer multiple of coin[i]. For example, In the given problem, we'll fill M[0][2] by 1 (as one {2} is needed to make 2), M[1][6] by 2 (as {3, 3} is required to make 6). We can follow this pattern for the final solution.

xxxxxxxxxx
 
// Fill the array using the following rule.
​
Routine: Solve
Input: Coin array of size N, denomiation amount
Required for intermediate results: Matrix M of size Nx(amount+1)
​
Base case:
1. For all rows with column index j=0, set M[i][j]=0
2. For each row i=0..(N-1)
    a. If a column index (j>0) is an integer multiple of coin[i], i.e., if (j mod coin[i] == 0) 
        then M[i][j] = j/coin[i]
        else M[i][j] = inf
        
Recursive case:
1. for each row i=1..(N-1)
    a. for each col j=0..amount
            i. M[i][j] = min(M[i-1][j-k*coin[i] ]+k), where k is 0..floor(j/coin[i])
2. return M[i-1][amount]

Filling the Matrix

The figure shows how the pseudo-code works. Initially the matrix M is empty. Then, for each cell, if a coin denomination (column index j) is an integer multiple of the coin for that row, then fill up that cell with j / coin[i].

Next, fill the matrix row by row as shown in the figure. As an example, for i=2, j=11, the value of the matrix is:

SNIPPET

1M[2][11] = min(M[1][11],M[1][6]+1,M[1][1]+2) = min(4,2+1, inf+2) = 3

Coding

Now you should be ready to write the code for the coin change problem. To represent infinity/inf, you can use a very large number for which you are sure that it is larger than any possible result. For example, I suggest taking inf as the highest denomination/Txhighest. If no combination is possible, then the coinChange function should return -1. You may assume that the input array is sorted, but I would encourage you to sort the array, if necessary.

The code should have a complexity of O(NT * T/coin[0]) as there are N(amount+1) cells in the matrix. For each cell, a minimum is computed from a list of at the most amount/coin[0] items. As the number of comparisons to compute the minimum won't change, even if we increase the number of unique coins, hence we can take amount/coin[0] as a constant, resulting in a time complexity of O(NT).

One Pager Cheat Sheet

The task is to find the minimum number of coins that add up to a given denomination amount using dynamic programming, with a given set of coins of different denominations and an infinite supply of each one.
This problem can be solved using an efficient dynamic programming algorithm to efficiently explore all possible combinations and find the one with a minimum number of coins.
Boldly dynamic programming is used to define an array matrix M, whose size is N*(amount+1) to store the intermediate results of the coin change problem.
The figure shows how the Matrix M is filled row by row, with each value in the cell equaling the minimum number of coins required to pay the amount, given the coin denomination for that row.
Write code to solve the coin change problem in O(NT) time, where inf is the highest value of the coin denominations and -1 is returned if no combination is possible.

This is our final solution.

To visualize the solution and step through the below code, click Visualize the Solution on the right-side menu or the VISUALIZE button in Interactive Mode.

xxxxxxxxxx
}
 
var assert = require('assert');
​
function coinChange(coins, amount) {
  // Each memo[i] is the least amount of coins
  // that can make the value equal to the index value.
  const memo = Array(amount + 1).fill(Infinity);
  memo[0] = 0;
​
  for (let i = 1; i <= amount; i++) {
    for (const coin of coins) {
      if (i - coin >= 0) {
        memo[i] = Math.min(memo[i], memo[i - coin] + 1);
      }
    }
  }
  return memo[amount] === Infinity ? -1 : memo[amount];
}
​
try {
  assert.equal(coinChange([2, 3, 5], 11), 3);
​
  console.log('PASSED: ' + 'First Test: coinChange([2, 3, 5], 11)');
} catch (err) {
  console.log(err);
}
​
try {
  assert.equal(coinChange([2, 3, 5, 7], 17), 3);
​
  console.log('PASSED: ' + 'Second Test: coinChange([2, 3, 5, 7]');
} catch (err) {
  console.log(err);

You're doing a wonderful job. Keep going!

If you had any problems with this tutorial, check out the main forum thread here.