How to Solve the Coin Change Problem

This problem can be solved recursively. The idea behind the recursive solution is to try out all possible combinations that add up to amount, and pick the solution with a minimum number of coins. You might think that trying out all possible combinations means that we are opting for an exponential time complexity solution-- not the case!

Exponential time complexity problems aren't useful in real life, as the run-time will often kill the application. What we can do instead is to try out all possible combinations intelligently using dynamic programming. Dynamic programming will drastically cut down our search time for finding the solution.

Let me illustrate the idea behind the search for the solution using a simple example. Suppose we are given the coins [2, 3, 5] and amount = 11. Let's now look at the figure that shows us the solution:

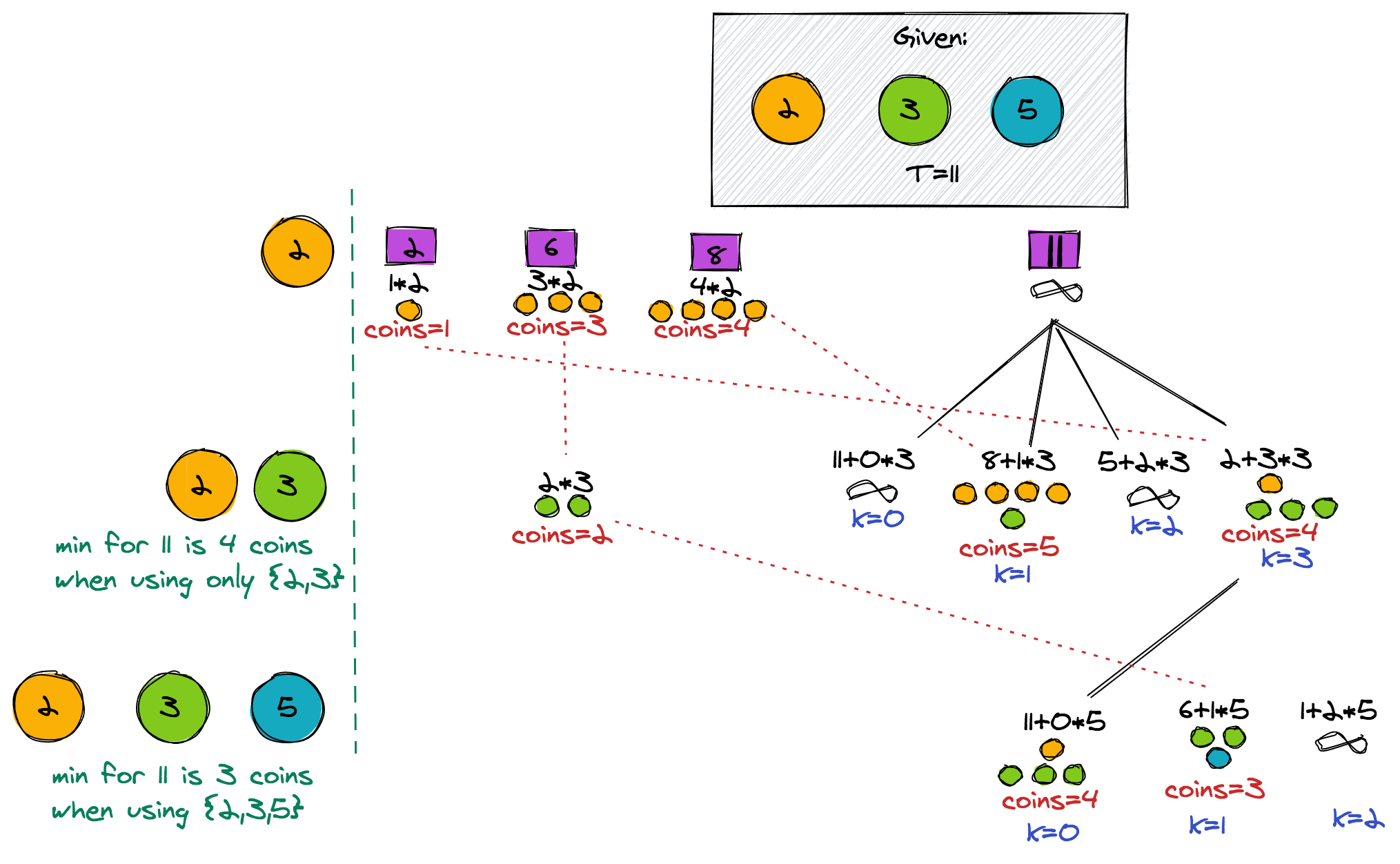
The idea here is to build a tree by making combinations with only coin {2} (level 1 of the tree). Then, we can make use of this information to make all combinations with {2, 3} (the second level of the tree). Finally, we'll all combinations with {2, 3, 5} in the third level. Notice that we cannot make 11 with just {2}, so we have infinity as the answer.

Going down one level, we make various combinations of 11 by adding the coin 3 in 4 ways (for example, we can add up {}, {3}, {3, 3}, or {3, 3, 3}. For these four branches, information from the previous level is required. For example, when no coin 3s are added, we need to know the optimal way to make 11 from just coin 2. When only one coin 3 is added (from, say, {3}), then we need to know the optimal way to make 8 from just coin 2. When {3, 3} is added, we need to know the optimal way to make 5 from just coin 2. The same is the case with {3, 3, 3}. For this level, pick the minimum number of coins (i.e. 4), with the combination {2, 3, 3, 3}.

This same idea is repeated with {2, 3, 5}. We can make 11 by adding coin 5 zero times, one time, or two times-- and pick the minimum from this list. We have as many "levels" as the number of coins. We also need to know the optimal way of making denominations for 1..amount. In this example, you can see that we needed denominations 2, 6, 8 starting at the first level of the tree. It is important to note that only the optimal number of coins has to be stored for each level.