Good afternoon! Here's our prompt for today.
A clear path is a path in a binary grid from the top-left cell (0, 0) to the bottom-right cell (n - 1, n - 1) such that,
- All the visited cells of the path have a value of 0.
- All the adjacent cells of the path are
8-directionally connected(they are different and share an edge or a corner).
Consider an n x n binary grid grid. Find the length of the shortest clear path in the matrix. If there is no clear path, return -1.
Here,
n = row = column. The length of a clear path is the number of visited cells through this path.
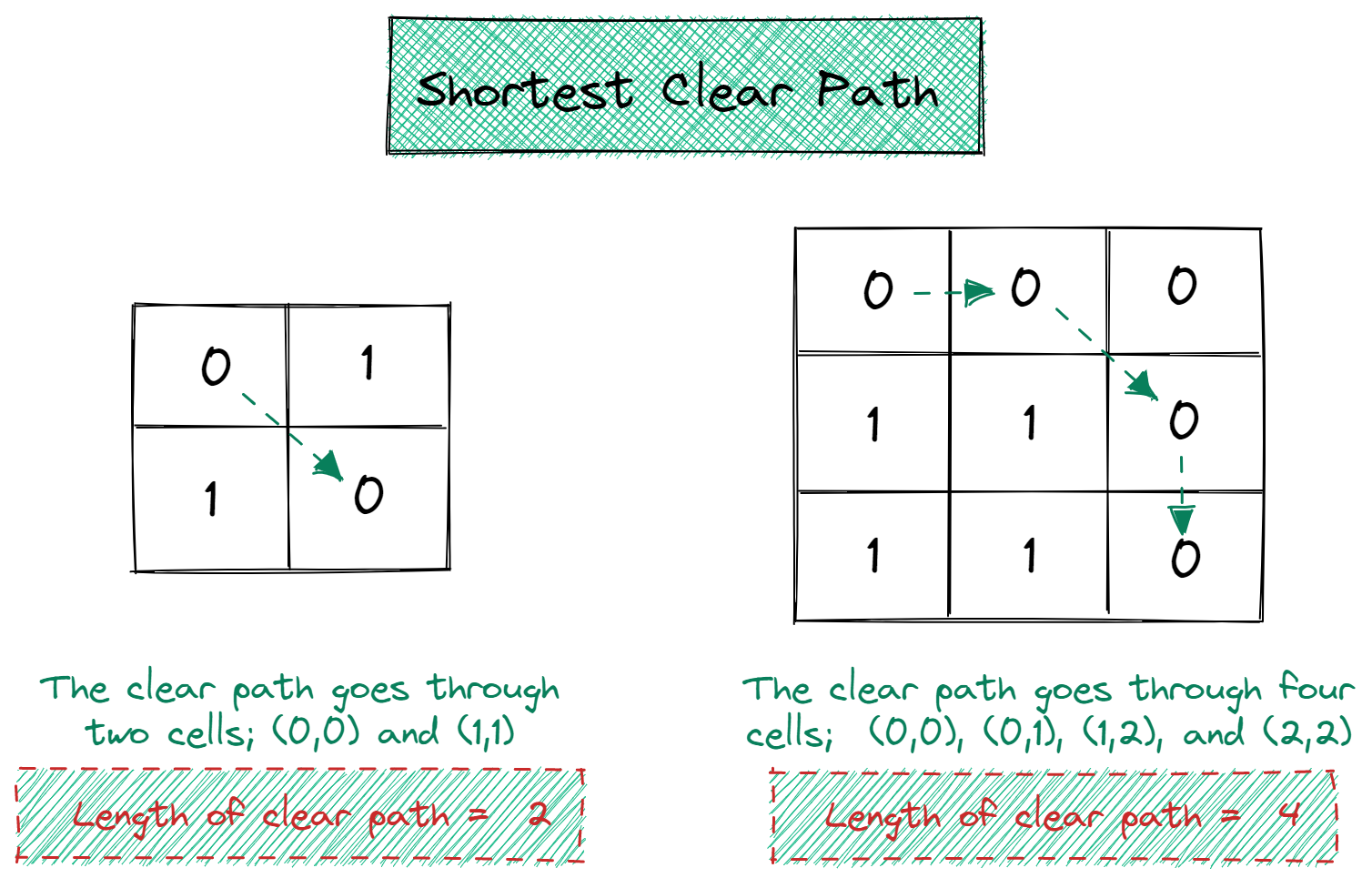
For example, consider the grids in the image above. For the 2x2 grid, only one clear path exists, and that is the shortest clear path. For the 3x3 grid, two clear paths exist. One has a length of 5 (if we include the top-right element), and the other has a length of 4 (as shown in the image). We choose the path with a shorter length, that is, the path of length 4.
Constraints
n == grid.lengthn == grid[i].length1 <= n <= 100grid[i][j]is0or1
Try to solve this here or in Interactive Mode.
How do I practice this challenge?
xxxxxxxxxx console.log('PASSED: ' + "`shortestClearPath([[1,0,0],[1,1,0],[1,1,0]])` should return `-1`");var assert = require('assert');function shortestClearPath(grid) { return;}try { assert.equal(shortestClearPath([ [0, 1], [1, 0] ]), 2); console.log('PASSED: ' + "`shortestClearPath([[0,1],[1,0]])` should return `2`");} catch (err) { console.log(err);}try { assert.equal(shortestClearPath([ [0, 0, 0], [1, 1, 0], [1, 1, 0] ]), 4); console.log('PASSED: ' + "`shortestClearPath([[0,0,0],[1,1,0],[1,1,0]])` should return `4`");} catch (err) { console.log(err);}try {We'll now take you through what you need to know.
How do I use this guide?
Let's think of the grid in this problem as an undirected graph. For each node of the graph, we must check all its adjacent nodes to find a clear path. Can you recall a graph algorithm that can be used for checking adjacent nodes and shortest paths? One of our two favorite graph traversal algorithms fits this criterion, which is the Breadth First Search (BFS) algorithm.
Now, of course, the BFS algorithm needs to be modified so that it can be applied to the binary grid in the problem. The core approach for traversal is still the same, by adding and removing grid cells (instead of tree nodes) into the queue. To make our task easier, let's first consider some invalid cases.
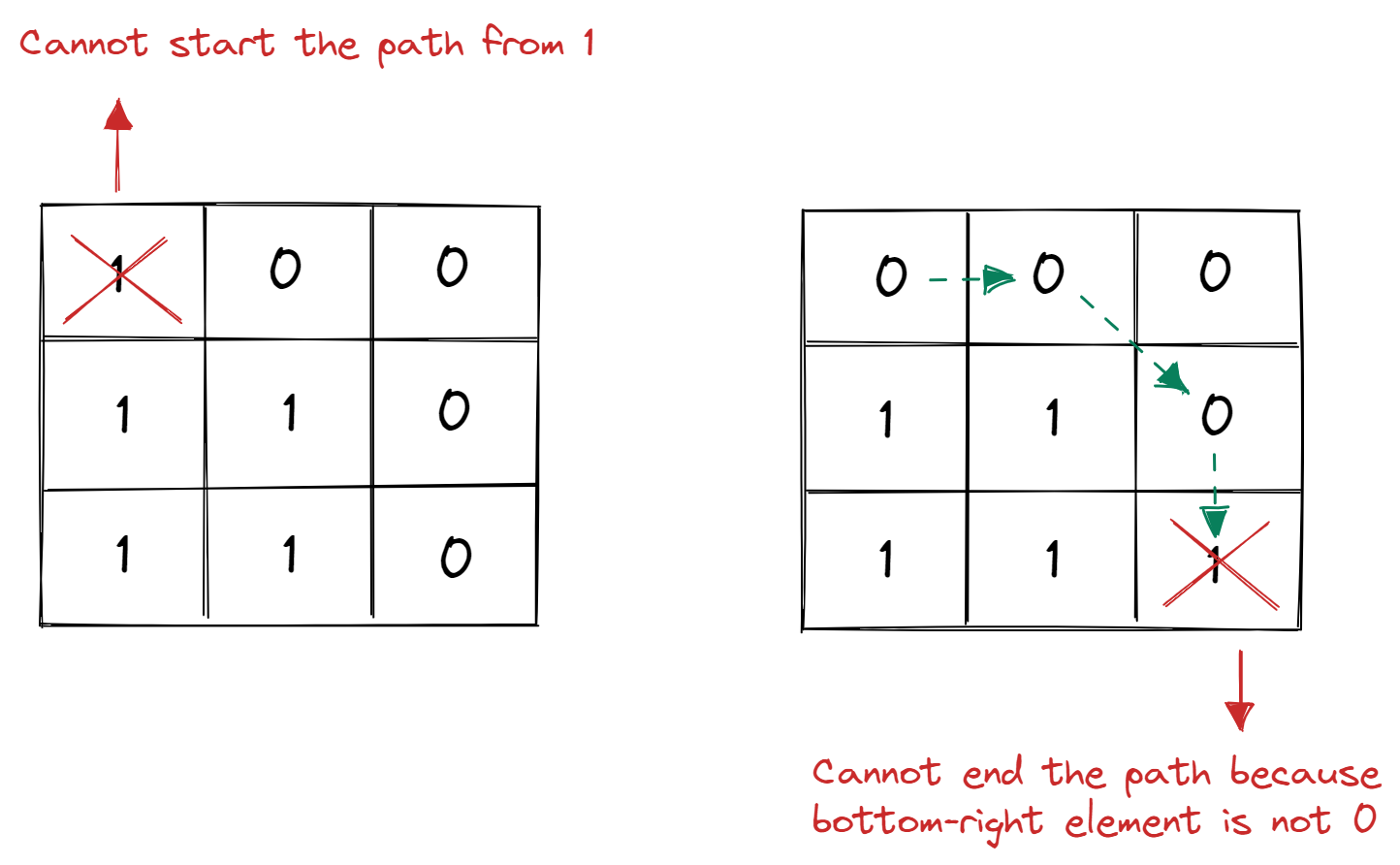
- If we have a grid that has the top-left element as 1, then there will be no clear path (cannot start the path from 1).
- If a grid has the bottom-right element as 1, then there will be no clear path (cannot end the path).
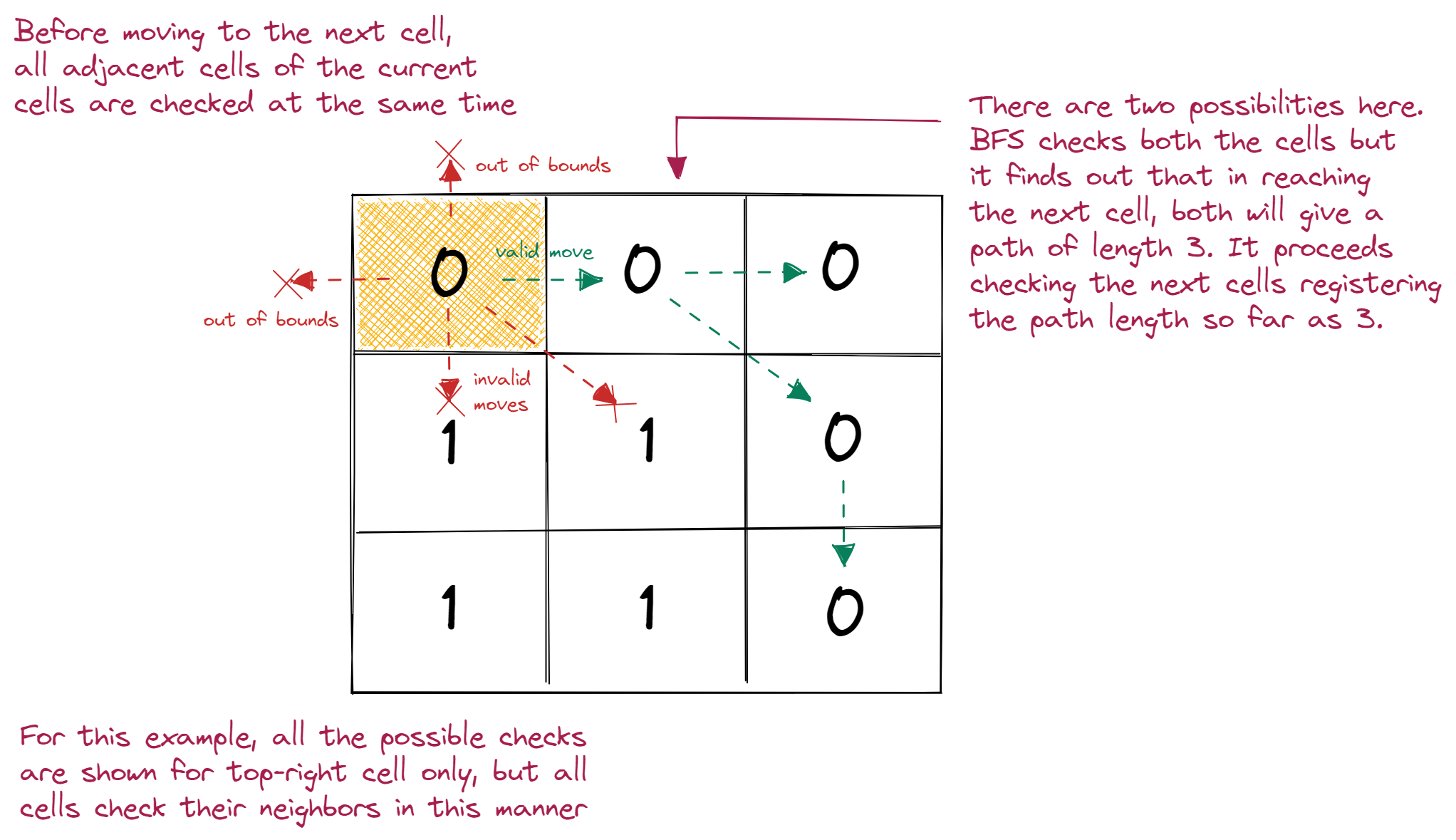
Now let's get back to our main algorithm. To make the BFS work for a grid, we first define an array of all the possible directions that we can move in (up, down, diagonals), as unlike graphs grids are navigated by incrementing the x and y positions. We must also modify how we store elements in our plain old queue. Along with the value at each cell, the positions of cells are also stored. In this way, by incrementing the x and y values, we can move in the eight possible directions. As we traverse through these eight directions, we check for a couple of things,
- The value at the next cell (it should be 0, we do not want to go to cells with a value of 1)
- The
xandyvalues of the next cell (they should not be out of bounds of the grid)
If the above conditions are met, the position and values of the next cell are successfully added to the queue. However, we would like to ensure that the current cell is not traversed again and that it does not show up while we check the eight possible directions for any other cell. To prevent such a case from occurring, the value at the current cell is changed from 0 to 1 to indicate that this position has already been visited. This process is repeated until we reach the bottom-right cell of the matrix.
Try this exercise. Click the correct answer from the options.
What could be another method to check that a cell is not visited twice?
Click the option that best answers the question.
- Add extra conditions
- Use a dictionary/hashmap
- Use a set
- None of the above
Let's test your knowledge. Fill in the missing part by typing it in.
The time complexity of this problem is _
Please write the answer in terms of m, n, where m = rows, n = columns of the grid
Write the missing line below.
Build your intuition. Is this statement true or false?
A DFS based solution to this problem would have the same time complexity as the BFS based approach.
Press true if you believe the statement is correct, or false otherwise.
One Pager Cheat Sheet
- Find the length of the shortest clear path in an
n x nbinary grid, or-1if no clear path exists. - We can use the
Breadth First Search (BFS)algorithm to find a clear path between all adjacent nodes in the undirected graph. - We can modify Breadth-First Search to find the
shortest clear pathin a binary grid, taking care to consider someinvalid caseswith the top-left and bottom-right elements. - We are using a modified Breadth-First Search to traverse through a
grid, storing values at each cell and adding/marking positions of each cell to/from ourqueueto ensure that we find the shortest clear path from the top-left cell to the bottom-right cell. - By using a set to
indexand store the cells that have been visited, it is possible to ensure that no cell is visited twice as sets do not allow for duplicates of unique elements. - The algorithm must traverse an
m x ngrid, resulting in O(m*n) time complexity. - The time complexity of BFS is
O(m×n)and of DFS isO(m+n)in a graph withmvertices andnedges.
This is our final solution.
To visualize the solution and step through the below code, click Visualize the Solution on the right-side menu or the VISUALIZE button in Interactive Mode.
xxxxxxxxxx}var assert = require('assert');function shortestClearPath(grid) { let m = grid.length; let n = grid[0].length; if (grid[0][0] === 1 || grid[m - 1][n - 1] === 1) { return -1; } let directions = [ [0, 1], [0, -1], [1, 0], [-1, 0], [1, 1], [1, -1], [-1, 1], [-1, -1] ]; let queue = [ [ [0, 0], 1 ] ]; grid[0][0] = 1; while (queue.length > 0) { let [cellPosition, pathLength] = queue.shift(); let x = cellPosition[0]; let y = cellPosition[1];Alright, well done! Try another walk-through.
If you had any problems with this tutorial, check out the main forum thread here.

