AlgoDaily - Stock Buy and Sell Optimization

Good morning! Here's our prompt for today.

This is a classic technical interview question that I've seen a number of times in real life interviews. Let's say you're given an array of stock prices, with each element being an integer that represents a price in dollars.

SNIPPET

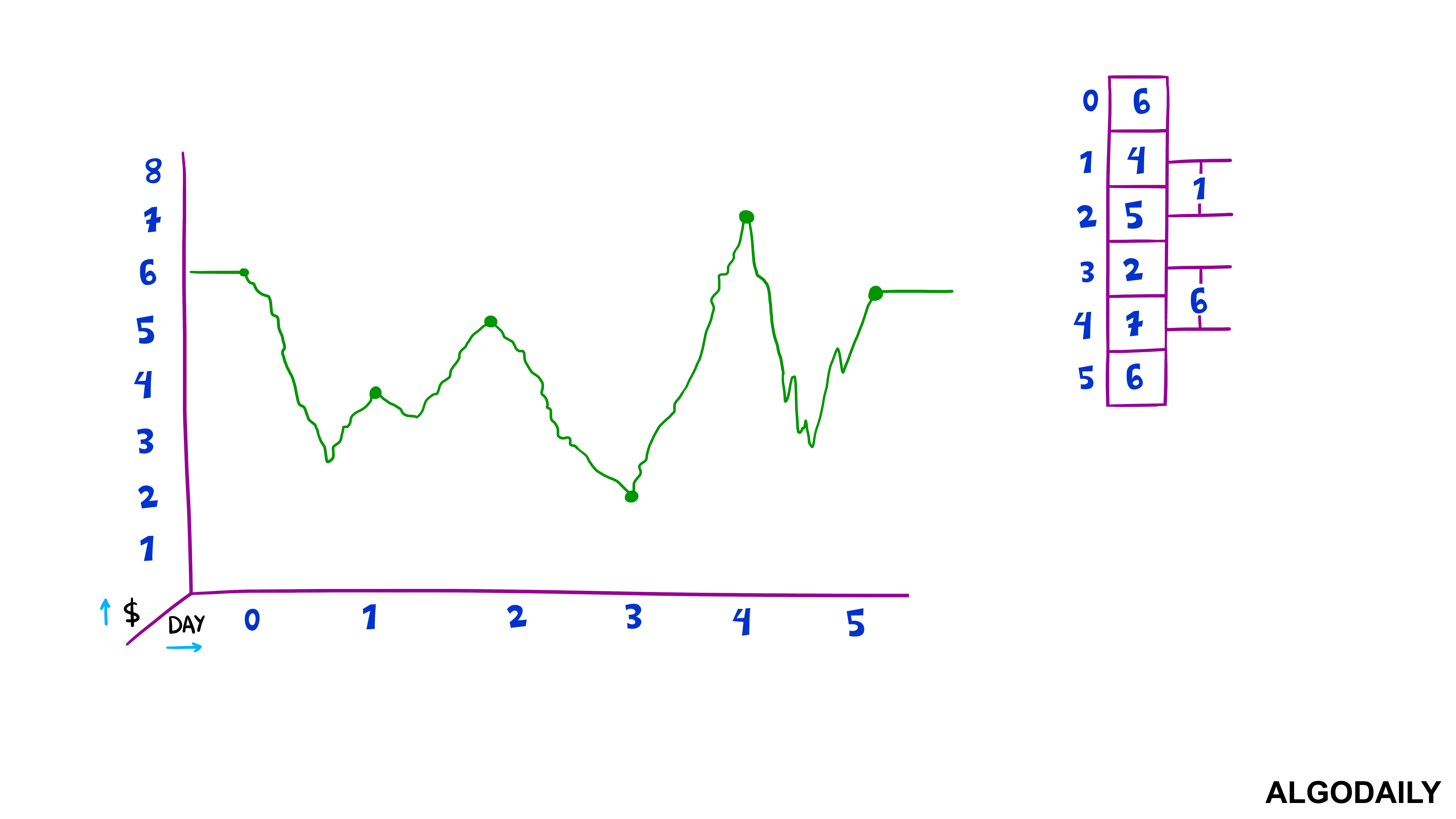
1[ 10, 7, 6, 2, 9, 4 ]

Each index of the array represents a single day, and the the element at that index is the stock price for that given day. This means that the array below represents:

1let prices = [10, 7, 6, 2, 9, 4];
2// Day 0 - a price of `$10`
3// Day 1 - `$7`
4// Day 2 - `$6` (and so on...)

Given the ability to only buy once and sell once, our goal is to maximize the amount of profit (selling price - purchase price) that we can attain and return that value. Note the only caveat is that that we cannot sell a stock before we buy it, which is important in identifying a solution.

Can you write a stock optimizer method called stockOptimizer? See the following examples for further clarification:

1stockOptimizer([10, 7, 6, 2, 9, 4]);
2// 7

For the above example, the max profit is made when we buy on day/index 3 (when the price is 2) and sell on day/index 4 (when the price is 9). 9 - 2 gives us 7, which is returned by the function. Let's do another example.

1stockOptimizer([9, 8, 6, 5, 3]);
2// 0

From a quick glance, it seems like there's enough price differences to generate a profit. However, notice that the price drops every day, and thus we can't have a profit since we're required to buy before selling.

Constraints

Length of the given array <= 100000
The array will always consist of non zero integer (including 0)
The maximum price would be <= 2147483647
Expected time complexity : O(n)
Expected space complexity : O(1)
The array would always contain more than 1 element

Try to solve this here or in Interactive Mode.

How do I practice this challenge?

xxxxxxxxxx
    'PASSED: ' + 'stockOptimizer([14,3,16,8,9,7,8,18,15,10,9]) should return 15'
 
var assert = require('assert');
​
function stockOptimizer(prices) {
  // Fill in this method
  return prices;
}
​
try {
  assert.deepEqual(stockOptimizer([14, 20, 9]), 6);
​
  console.log('PASSED: ' + 'stockOptimizer([14,20,9]) should return 6');
} catch (err) {
  console.log(err);
}
​
try {
  assert.deepEqual(stockOptimizer([5, 20, 15, 13, 3, 15, 5, 10]), 15);
​
  console.log(
    'PASSED: ' + 'stockOptimizer([5,20,15,13,3,15,5,10]) should return 15'
  );
} catch (err) {
  console.log(err);
}
​
try {
  assert.deepEqual(stockOptimizer([1, 6, 11, 2]), 10);
​
  console.log('PASSED: ' + 'stockOptimizer([1,6,11,2]) should return 10');

Tired of reading? Watch this video explanation!

To change the speed of the video or see it in full screen, click the icons to the right of the progress bar.

Here's how we would solve this problem...

How do I use this guide?

Identifying the Problem

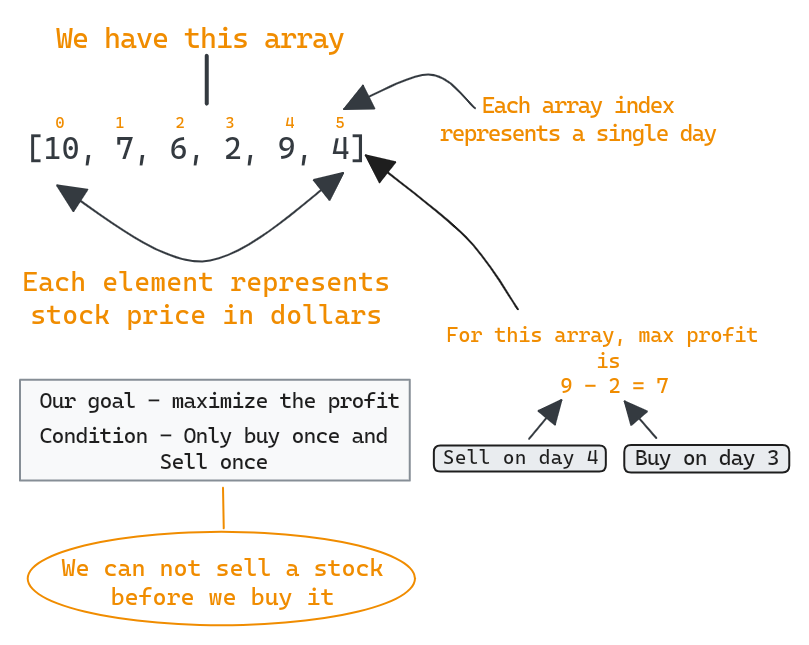
We want to figure out the greatest possible profit from buying and selling a stock. The sequence of stock prices is represented by an array, and each element indicates the price on a particular day.

Starting with Basic Understanding

Initially, we might think that finding the maximum and minimum prices would suffice. However, the requirement that we must buy before selling adds a twist.

Realizing the Complexity

We realize that the order of prices matters, so the minimum price must occur before the maximum price.

Understanding the Challenge

The problem isn't as straightforward as finding the largest and smallest elements. Here's why:

Buying before Selling Rule: We must buy before selling, so order matters. Simply finding max and min values is not enough; we need to ensure that the min value comes before the max.

Crafting the Solution

Given the constraint of buying before selling, we can sketch out a plan as follows:

Iterate Through Days: We'll iterate through each element (day) in the array.
Compare with Future Days: At each day, we'll check the difference between the price of that day and only the prices on days after it.
Nested Loops: This can be achieved with a simple nested for-loop.
- The first loop goes through all the days.
- At each day, a second loop (starting from j = i + 1) compares the price of the day to only the prices on subsequent days.
Maximize Profit: During the iteration, we'll keep track of the minimum price so far and the maximum profit obtainable. The difference between the current price and the minimum price will help us find the maximum profit.

Why This Approach Works

Adheres to the Rule: By comparing a price only with prices on subsequent days, we ensure that buying occurs before selling.
Efficiency: This approach leads to a solution within the given constraints.

xxxxxxxxxx
 
function stockOptimizer(prices) {
  let maxDiff = 0;
  for (let i = 0; i < prices.length; i++) {
    for (let j = i + 1; j < prices.length; j++) {
      let newDiff = prices[j] - prices[i];
​
      if (newDiff > maxDiff) {
        maxDiff = newDiff;
      }
    }
  }
​
  return maxDiff;
}
​
console.log(stockOptimizer([2, 5, 15, 9]));

Nested Loops: A Concern

The given code uses nested loops, resulting in a time complexity of $O (n^{2})$ , where $n$ is the length of the array. In the worst case, this could lead to sluggish performance, particularly for larger datasets. In a real-world scenario, efficiency often matters a lot, so we'd prefer to optimize the code.

A More Efficient Approach

Can we achieve the same result with just one loop, making it an $O (n)$ solution? Yes, we can! Let's break down how we can do this.

Try this exercise. Click the correct answer from the options.

What is the time complexity of the below brute force solution?

1function stockOptimizer(prices) {
2	let maxDiff = 0;
3	for (let i = 0; i < prices.length; i++) {
4		for (let j = i + 1; j < prices.length; j++) {
5			let newDiff = prices[j] - prices[i];
6
7			if (newDiff > maxDiff) {
8				maxDiff = newDiff;
9			}
10		}
11	}
12
13	return maxDiff;
14}
15
16console.log(stockOptimizer([2, 5, 15, 9]));

Click the option that best answers the question.

O(n)
O(n^2)
O(n^3)
O(1)

Whenever you are struggling for an answer, try to identify some pattern in the examples to exploit. A realization that may help is the fact that because the selling price must come after the buy price, we can start our iteration from the end of the array. What are the things we need to keep track of?

The realization that we can start our iteration from the end of the array opens up an interesting perspective on the problem. Let's break it down into a step-by-step process:

Reversing the Perspective

Why Iterate from the End?

Starting from the end allows us to look at the problem differently: instead of focusing on the buying price first, we can focus on the selling price.
This method still aligns with the problem constraint that selling must come after buying.

How This Approach Works

By iterating from the end, we're effectively looking at the future prices first and then determining the best buying price for those future selling prices.
We ensure that the selling price always comes after the buying price by updating our maxPrice only when we find a higher price as we move towards the beginning of the array.
It's still an $O (n)$ solution, as we're only iterating through the array once.

Build your intuition. Click the correct answer from the options.

Given an array of stock prices on an hourly basis throughout a day, calculate the max profit that you can make by buying and selling only once. Which of the following variables may be helpful in solving this problem?

Click the option that best answers the question.

An hourly profit amount
A maximum and minimum price
An hourly profit and minimum price
A daily minimum price

What will be helpful is finding a maximum difference so far (which is the profit) and the maximum price starting from the right. If we know the maximum price starting from the end, we can calculate the difference between that, and each subsequent element moving leftwards.

What this does is ensure that we're accounting for the order of the prices. With each step towards the front of the array, we can find a new maximum profit (maxProfit) based on the new current max price (curMax) that we encounter using something like the below logic:

1if (temp > curMax) {
2    curMax = temp;
3}

Running through iterations gives us a tangible sense of how the algorithm works, especially when we start from the end of the array. Let's analyze the iterations on the given example prices = [ 10, 7, 6, 2, 9, 4 ]:

Iteration Overview

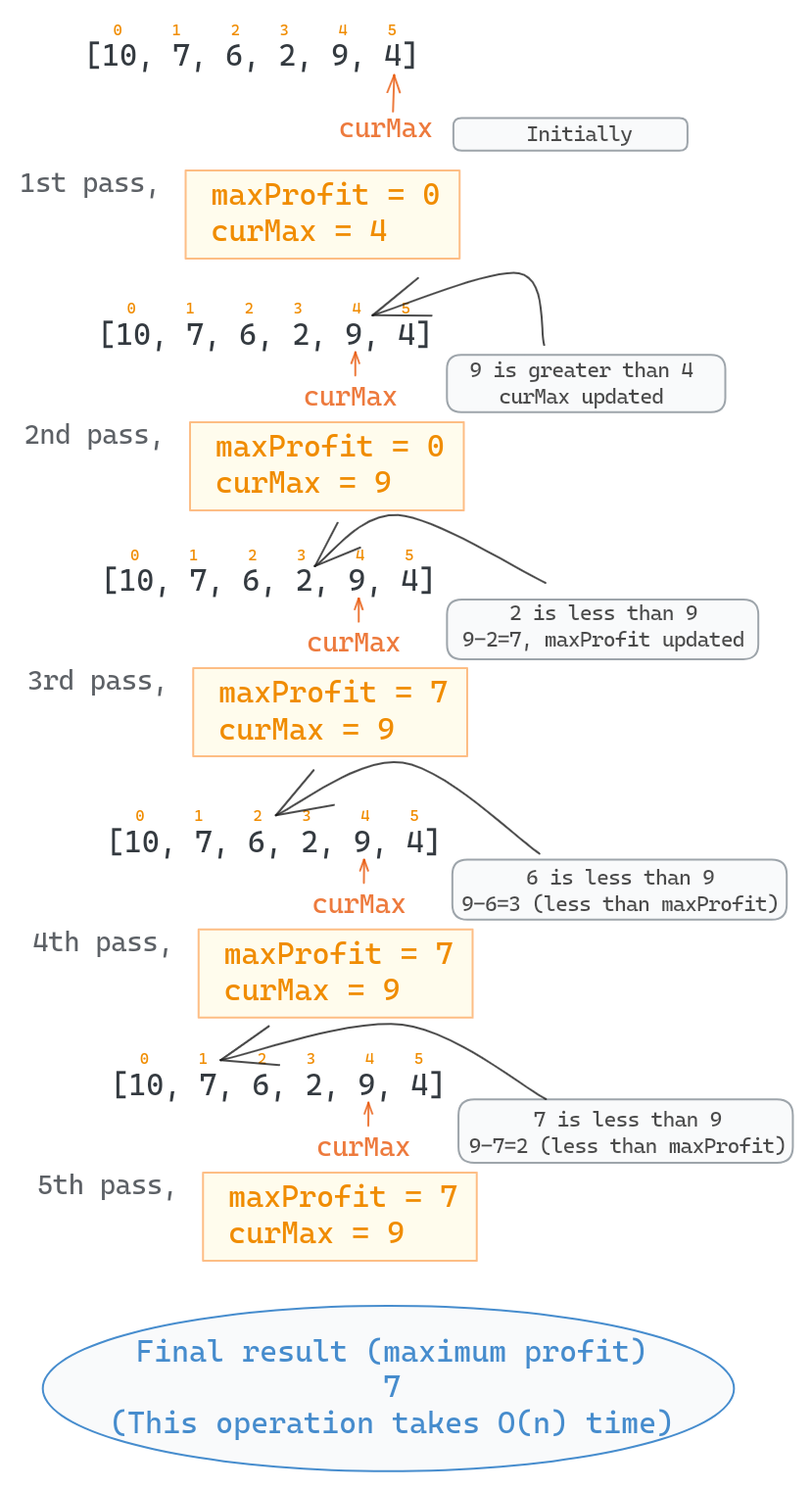
Initialization:

maxProfit = 0: the maximum profit found so far.
curMax = 4: the current maximum price (initialized with the last price in the array).

Iterative Passes:

1. First Pass (`[4]`):

There's only one element, so there's no profit to calculate.
maxProfit remains 0, curMax remains 4.

2. Second Pass (`[..., 9, 4]`):

curMax is updated to 9, as it's greater than the previous curMax.
maxProfit remains 0 as we have not found a suitable buying price yet.

3. Third Pass (`[..., 2, 9, 4]`):

Potential profit is 9 - 2 = 7, so maxProfit is updated to 7.
curMax remains 9.

4. Fourth Pass (`[..., 6, 2, 9, 4]`):

Potential profit is 9 - 6 = 3, but it's less than the current maxProfit.
maxProfit remains 7, curMax remains 9.

5. Fifth Pass (`[..., 7, 6, 2, 9, 4]`):

Potential profit is 9 - 7 = 2, but it's less than the current maxProfit.
maxProfit remains 7, curMax remains 9.

Result:

The maximum profit of 7, achieved by buying at 2 and selling at 9.

Why This Works:

Selling Price Perspective: By starting from the end, we focus on potential selling prices first and find the corresponding best buying prices as we move towards the beginning of the array.
Efficient Tracking: The continual updates to curMax and maxProfit enable us to track the best selling price and corresponding profit efficiently in a single pass.

Summary:

By illustrating the steps through iterations, we can see how this reverse-traversal algorithm systematically calculates the best profit by considering each day as a potential selling day and finding the best corresponding buying day. This approach is efficient and aligns with the constraints of the problem, making it a powerful solution. It also showcases how a simple shift in perspective can lead to an elegant solution.

The key is that our curMax may or may not be the max that gets us the maximum profit. We still need to compare future curProfits that we calculate with our max profit thus far.

Let's test your knowledge. Fill in the missing part by typing it in.

What line would get us the max profit for each day?

SNIPPET

1const prices = [ 10, 7, 6, 2, 9, 4 ];
2let curMax = prices[prices.length - 1];
3let maxProfit = 0;
4for (let i = prices.length - 1; i >= 0; i--) {
5	const temp = prices[i];
6	______________
7		curMax = temp;
8	}
9	const curProfit = curMax - temp;
10	if (curProfit > maxProfit) {
11		maxProfit = curProfit;
12	}
13}
14console.log(maxProfit);

Write the missing line below.

One Pager Cheat Sheet

The interview question asks to create a stockOptimizer method to maximize profit from an array of stock prices, by buying once and selling once, given the constraint that a stock cannot be sold before it is bought, with input array length <= 100000, non-zero integer rates and a maximum price <= 2147483647, within a time complexity of O(n) and space complexity O(1).
In order to calculate the greatest possible profit from buying and selling a stock represented by an array of prices, one must iterate through each day, comparing the price of that day and only the prices on subsequent days using nested loops and adhering to the rule of buying before selling, all the while tracking the minimum price so far and the maximum profit obtainable, which is the difference between the current price and the minimum price.
The code utilizes nested loops with a time complexity of O(n^2), which can slow performance for larger datasets, but can be optimized to an O(n) solution by using only one loop.
The provided solution has a time complexity of O(n^2) due to the use of nested loops, which means for every additional input, the algorithm needs to perform work proportional to the square of the number of inputs.
When trying to find an answer, identifying patterns can be helpful, and a useful realization is that we can iterate from the end of an array, focusing first on the selling price before finding the best buying price by updating the maxPrice while moving towards the start, which still provides an O(n) solution.
The problem involves iterating from the end to the beginning of an array, adjusting the maxProfit (highest profit at a specific hour) and minPrice (lowest price thus far) to calculate the maximum possible profit while ensuring the selling price always comes after the buying price.
To maximize profit in stock trading, it's beneficial to find the maximum difference (profit) and the maximum price from right to left in an array, keeping the order of prices, and updating the current max price (curMax) and the maximum profit (maxProfit) as we move towards the front of the array with conditional programming logic.
Through iterations of an algorithm on a sample array prices = [ 10, 7, 6, 2, 9, 4 ], running from the array's end, variables maxProfit and curMax are updated comparing potential profits and maximum price respectively, resulting in a maximum profit of 7, achieved by purchasing at the price of 2 and selling at 9.
The described reverse-traversal algorithm effectively calculates the best profit in a selling price perspective by considering each day as a potential selling day, and uses curMax and maxProfit for efficient tracking of the best selling price and corresponding profit.
The algorithm computes the maximum profit from stock trading by tracking the highest selling price (curMax) as it scans the array of daily stock prices in reverse, and continually comparing the potential profit (curProfit) with the current maximum profit (maxProfit) to ensure the highest possible profit is chosen, resulting in maxProfit representing the best attainable profit.

This is our final solution.

To visualize the solution and step through the below code, click Visualize the Solution on the right-side menu or the VISUALIZE button in Interactive Mode.

xxxxxxxxxx
}
 
var assert = require('assert');
​
function stockOptimizer(prices) {
  if (!prices.length) {
    return 0;
  }
  if (prices.length == 1) {
    return 0;
  }
  let curMax = prices[prices.length - 1];
  let maxProfit = 0;
  for (let i = prices.length - 1; i >= 0; i--) {
    const temp = prices[i];
    if (temp > curMax) {
      curMax = temp;
    }
    const curProfit = curMax - temp;
    if (curProfit > maxProfit) {
      maxProfit = curProfit;
    }
  }
  return maxProfit;
}
​
try {
  assert.deepEqual(stockOptimizer([14, 20, 9]), 6);
​
  console.log('PASSED: ' + 'stockOptimizer([14,20,9]) should return 6');
} catch (err) {
  console.log(err);
}
​

Alright, well done! Try another walk-through.

If you had any problems with this tutorial, check out the main forum thread here.

Constraints

Try to solve this here or in Interactive Mode.

Tired of reading? Watch this video explanation!

Here's how we would solve this problem...

Identifying the Problem

Starting with Basic Understanding

Realizing the Complexity

Understanding the Challenge

Crafting the Solution

Why This Approach Works

Nested Loops: A Concern

A More Efficient Approach

Try this exercise. Click the correct answer from the options.

Click the option that best answers the question.

Reversing the Perspective

Why Iterate from the End?

How This Approach Works

Build your intuition. Click the correct answer from the options.

Click the option that best answers the question.

Iteration Overview

Initialization:

Iterative Passes:

1. First Pass (`[4]`):

2. Second Pass (`[..., 9, 4]`):

3. Third Pass (`[..., 2, 9, 4]`):

4. Fourth Pass (`[..., 6, 2, 9, 4]`):

5. Fifth Pass (`[..., 7, 6, 2, 9, 4]`):

Result:

Why This Works:

Summary:

Let's test your knowledge. Fill in the missing part by typing it in.

One Pager Cheat Sheet

This is our final solution.

Alright, well done! Try another walk-through.

Programming Categories

Popular Lessons

Constraints

Try to solve this here or in Interactive Mode.

Tired of reading? Watch this video explanation!

Here's how we would solve this problem...

Identifying the Problem

Starting with Basic Understanding

Realizing the Complexity

Understanding the Challenge

Crafting the Solution

Why This Approach Works

Nested Loops: A Concern

A More Efficient Approach

Try this exercise. Click the correct answer from the options.

Click the option that best answers the question.

Reversing the Perspective

Why Iterate from the End?

How This Approach Works

Build your intuition. Click the correct answer from the options.

Click the option that best answers the question.

Iteration Overview

Initialization:

Iterative Passes:

1. First Pass ([4]):

2. Second Pass ([..., 9, 4]):

3. Third Pass ([..., 2, 9, 4]):

4. Fourth Pass ([..., 6, 2, 9, 4]):

5. Fifth Pass ([..., 7, 6, 2, 9, 4]):

Result:

Why This Works:

Summary:

Let's test your knowledge. Fill in the missing part by typing it in.

One Pager Cheat Sheet

This is our final solution.

Alright, well done! Try another walk-through.

Programming Categories

Popular Lessons

1. First Pass (`[4]`):

2. Second Pass (`[..., 9, 4]`):

3. Third Pass (`[..., 2, 9, 4]`):

4. Fourth Pass (`[..., 6, 2, 9, 4]`):

5. Fifth Pass (`[..., 7, 6, 2, 9, 4]`):