Good morning! Here's our prompt for today.

Finding the Sum of Right Leaves in a Binary Tree

Imagine a family tree, but instead of tracking your relatives, it's tracking numbers. Each "person" in this tree has at most two "children," and some have none. We call these childless nodes "leaves," and your task is to find the sum of leaves that are on the right side of their "parent."

Visualizing the Problem

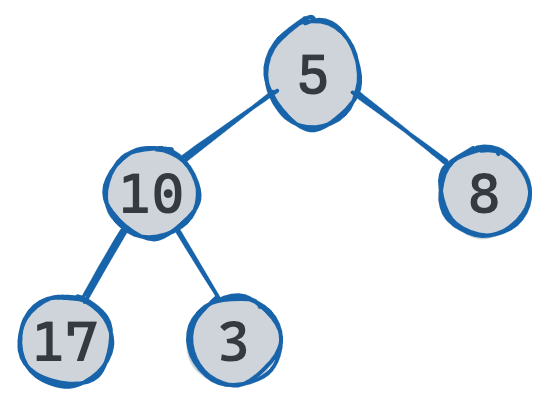
In this illustration, the right leaves are 8 and 3. Their sum would be 11.

Preparing the Groundwork

Before diving into the solution, let's first establish what a Node in this tree looks like. We assume all nodes, even the root, follow this structure:

1class Node {
2	constructor(val) {
3		this.value = val;
4		this.left = null;
5		this.right = null;
6	}
7}

Constraints to Keep in Mind

• The tree has a maximum length of 100,000 nodes.
• All node values are integers, ranging from -2000 to 2000.
• The function should run in O(n) time complexity.
• The space complexity should be O(n) considering the call stack.

Function Signature

You need to implement the following function:

1function sumOfRightLeaves(root) {
2  return root;
3}

Understanding the Challenge

The function takes in the root node of the tree as an argument. Your goal is to traverse the tree and sum up all the right leaves.

So, how do we do that? Let's dive into the solution next.

Try to solve this here or in Interactive Mode.

How do I practice this challenge?

xxxxxxxxxx

  assertIsFunction(sumOfRightLeaves, '`sumOfRightLeaves` should be a function');

var assert = require('assert');

​

function sumOfRightLeaves(root) {

  // use array representation of stack

​

  // Fill in this method

  return root;

}

​

function Node(val) {

  this.val = val;

  this.left = null;

  this.right = null;

}

​

// Regular binary trees

var tree1 = new Node(4);

tree1.left = new Node(1);

tree1.right = new Node(3);

​

var tree2 = new Node(5);

tree2.left = new Node(10);

tree2.left.left = new Node(17);

tree2.left.right = new Node(3);

tree2.right = new Node(8);

​

// Binary search trees

var tree3 = new Node(6);

tree3.left = new Node(3);

Here's how we would solve this problem...

How do I use this guide?