
A Bird’s Eye View into Sliding Windows
Objective: In this lesson, we'll cover this concept, and focus on these outcomes:
- You'll learn what the sliding windows algorithm pattern is.
- We'll show you how and when to use sliding windows in programming interviews.
- We'll walk you through some examples.
A sliding window is a sublist or subarray that runs over an underlying data structure. The data structure is typically iterable and ordered, such as an array or a string.
At a high level, you can think of it as a subset of the two pointers method. It normally encompasses searching for a longest, shortest or optimal sequence that satisfies a given condition.
Most sliding windows problems can be solved in O(N) time and O(1) space complexity.
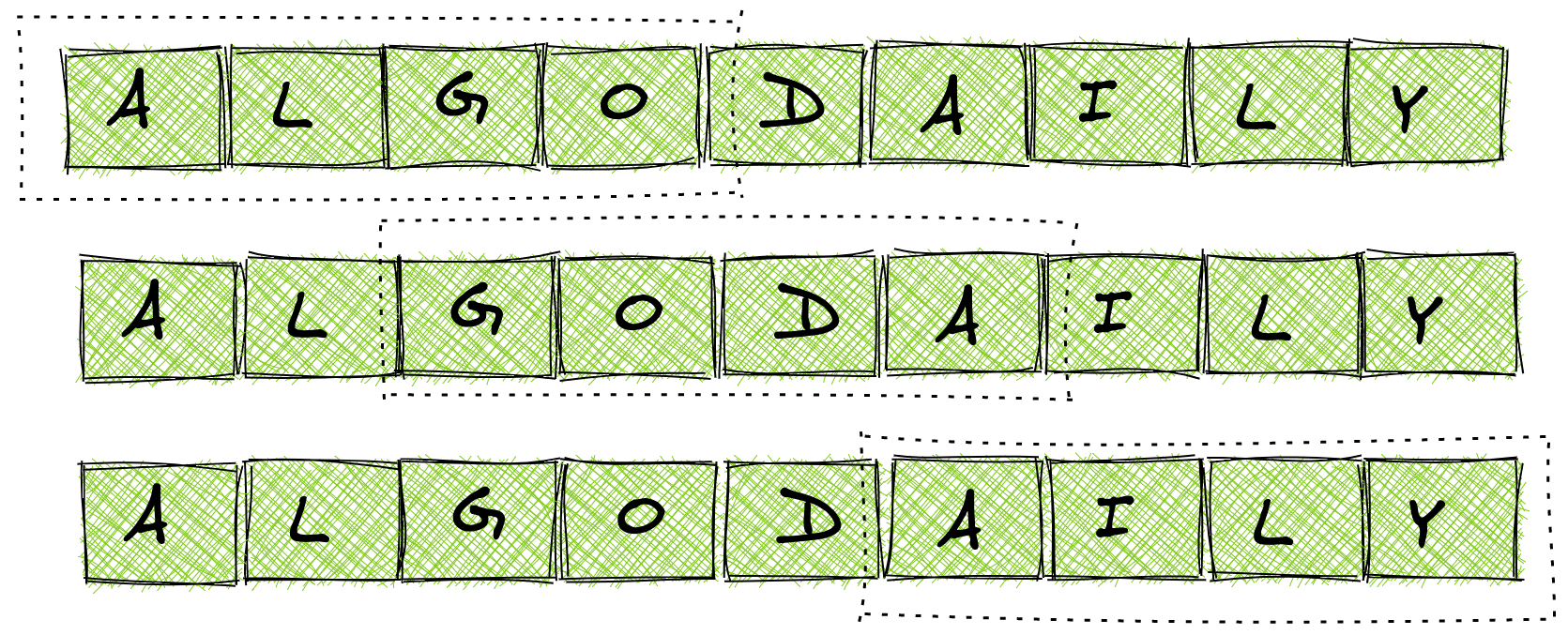
Say that we have an array that looks like this:
1const arr = ['a', 'l', 'g', 'o', 'd', 'a', 'i', 'l', 'y'];With the previous example, a sliding window with size 4 will look like the following at each iteration:
When to Use A Sliding Window
To identify problems where a sliding window can be helpful, look for a few properties:
- Whenever you need to calculate a running average
- If you want to formulate a set of adjacent pairs
- The problem involves an ordered data structure
- If you need to identify a target value in an array
- If you need to identify a longest, shortest, or most optimal sequence that satisfies a given condition in a collection
Let's say we had a string and some characters. We want to find the longest substring (a piece of the string with the same order of characters) containing all of those characters.
1String: "ADOBECODEBANC"
2Characters:"ABC"
3
4In the above example, it would be "ADOBEC" because it contains A, B, and C.The brute force way to approach this would be to iterate through the string, while looking at all the substrings of length 3. Then, we'd check to see if they contain the characters that you're looking for.
And then, if you can't find any substring of length 3, then try all substrings of length 4, and 5, and 6, and so on. You continue until you try options reaching the length of the string. But if you reach that point, you already know that the characters "ABC" are contained within it-- seems inefficient!
Furthermore, this approach is not very optimal as it runs in quadratic time or O(N²) time complexity. We would want a more optimal solution!
This is where the idea of a sliding window would come in.
The window would represent the current section of the string that you are looking at (which substring you're examining). It would have 2 pointers, one representing the start of the window and one representing the end.
1Left pointer at 'A' represents start
2Right pointer at 'O' represents end
3
4A D O B E C O D E B A N C
5
6^ ^With these pointers, we need to grow our window until we have a valid substring that contains all the characters we are looking for. Then shrink the window until we no longer have a valid substring.
This is the basic idea behind sliding windows! However, let's go into a more detailed example to cement this idea.
More detailed Example
The best way to develop the intuition behind how a sliding window works is via an example.
Let's hypothetically say we had a string “HGFDSAXZBJKC” and wanted to find the minimum substring containing all characters in “ABKC”. The sliding window technique would provide us with the necessary steps to accomplish this.
A Brute Force Approach
Given this problem, how might you solve it in a naive way without using a sliding window? Well, like I mentioned before with the brute force approach, you could scan through the entire string “HGFDSAXZBJKC” to test against all substrings of length 4. This is because “ABKC”, our "dictionary" of sorts, is 4 letters long, and takes into account the case where a substring consisting of "ABKC" is immediately found.
Provided you found all 4-letter substrings, you would then need to check each of them to figure out if they have all the characters that you need.
If you are unable to find all of required characters in the substrings of length 4 (meaning the minimum is longer than 4), we would then have to try alternate substrings of other lengths. This means we would then seek to look at substrings of greater lengths (5, 6, 7, and so on)-- with each possible length requiring a new iteration of the entire array.
Again, this can be extremely time consuming as it has a time complexity of O(N²). We're also missing out on information regarding how close we are to the ideal substring-- as we'll find out later, a sliding window can provide you with knowledge about how close we are to the desired range. We ascertain this from the location of the two pointers.
Using Sliding Window
So the brute force approach isn't the best. Luckily, we can utilize the sliding window technique. We will break it down, but first let's observe the entire solution with comments. s is the string, and req_chars is the substring containing all the required characters.
xxxxxxxxxxconsole.log(minWindow("abcalgosomedailyr", "ad"));function minWindow(s, reqChars) { // hash to keep account of how many required characters we've checked off // each key will represent a character in reqChars // we preset each to 1 and will look to lower it to 0 when each is fulfilled const hash = {}; for (let c of reqChars) { hash[c] = 1; }; // trackers that we need // this is a counter to measure string length against let counter = reqChars.length; let begin = 0; let end = 0; let substrSize = s.length + 1; let head = 0; while (end < s.length) { // continue running while there's more elements in `s` to process if (s[end] in hash) { // we've found a letter we needed to fulfill // modify the length counter, we can use this as part of our substring if (hash[s[end]] > 0) { counter -= 1; }The begin and end pointers represent the current "window" or section of the array that we are viewing, as displayed by:
xxxxxxxxxxlet begin = 0;let end = 0;We need a counter that checks to see if our current substring is valid or not. It'll start with the length of the required characters (since each needs to be present), and get decremented as required characters get processed.
xxxxxxxxxxlet counter = reqChars.length;We start counter off as the length of req_chars, and we'll decrement whenever we encounter a letter required. If we get to 0, it means it's a valid length.
1// from here, we increase begin pointer to make it invalid/valid again
2while (counter === 0) { // valid, we have what we needIn our initial example of “HGFDSAXZBJKC” and “ABKC”, we would have the following initialized tracker variables:
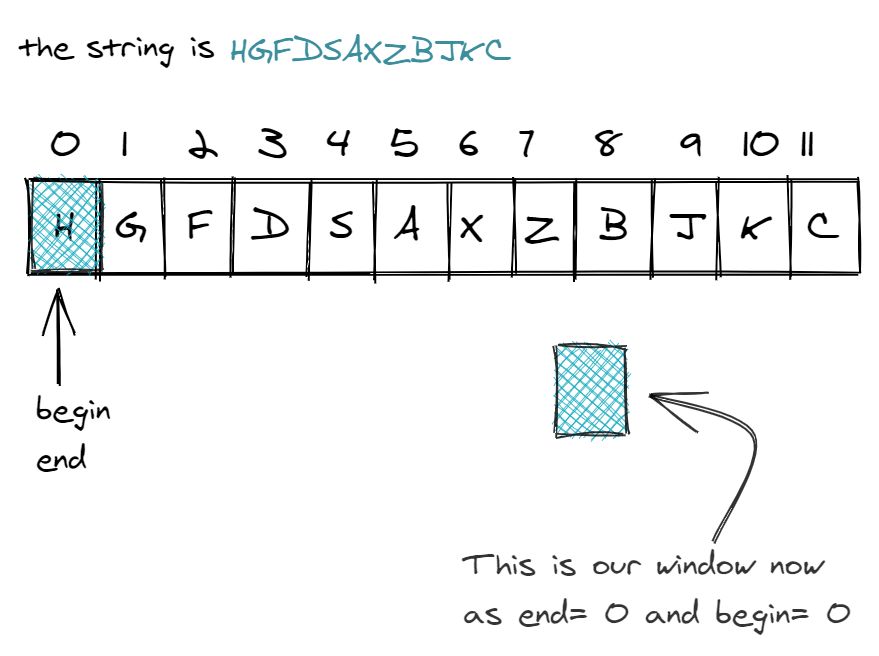
xxxxxxxxxxconst map = { 'A': 1, 'B': 1, 'K': 1, 'C': 1};let counter = 4;let begin = 0;let end = 0;let substrSize = 12;let head = 0;Now we test the window
One pointer/index corresponds to the beginning of your window, and the other corresponds to the end of the window. The first step is to move one pointer to find a valid window. This happens as we iterate through each letter, and run it through the following code block.
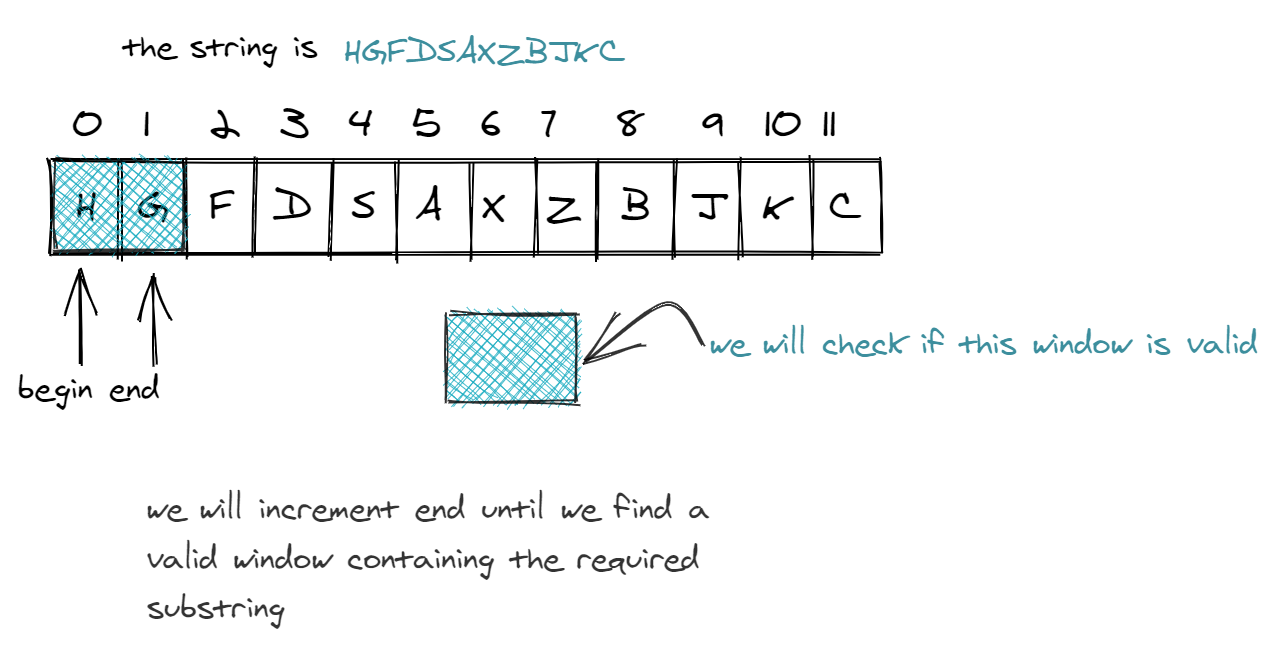
1// continue running while there's more elements in `s` to process
2if (s[end] in hash) { // we've found a letter we needed to fulfill
3
4 // modify the length counter, we can use this as part of our substring
5 if (hash[s[end]] > 0) {
6 counter -= 1;
7 }
8
9 // modify the dictionary to say we've gotten this character requirement
10 hash[s[end]] -= 1;
11}
12
13// Keep expanding the window once we are done contracting, try more substrings
14end += 1We do multiple things in the code block:
- Decrement our length
countervariable to say we have one less character requirement - Modify the dictionary to indicate we've fulfilled that character requirement
- Extend our window by incrementing
end(once we can't shorten from the front)
The idea is that you continue to grow your window until you find the string that is necessary to match the problem's conditions. This is done by moving the pointers outwards and expanding the scope of your window.
In our example of “HGFDSAXZBJKC” and “ABKC”, we would look at H and do the following operations. Observe as we step through the code via comments:
1if (hash[s[end]] > 0) { // we've found a letter we needed to fulfill
2// we're looking at `hash['H']`Wait, H isn't in the substring! So let's skip to an element that's actually in the substring-- looks like A:
1// we're looking at map['A'], it's currently 1 so proceed into the block
2 if (hash[s[end]] > 0) {
3 counter -= 1;
4 }
5
6 // modify the dictionary to say we've gotten this character requirement
7 // hash['A'] = 0
8 hash[s[end]] -= 1;
9
10 // check against our conditions
11
12 end += 1
13 # end is now 1, this will force us to step into checking the next letter
14}We'll proceed with the above logic until we get all the required letters that we needed, which is directed by while counter == 0:. Once we find the substring containing all the letters we need, we can then proceed since we've found a valid condition.
We're now sure that we've covered all the letters we need, but our window may be bigger than we need it to be. We can then shrink our window until we do not have a valid substring. Here's the code block for when we find a letter in the substring that isn't necessary.
xxxxxxxxxx// from here, we increase begin pointer to make it invalid/valid againwhile (counter === 0) { // valid, we have what we need // calculate the current substring size since we care about min if (end - begin + 1 < substrSize) { // overwrite if current substr is smaller substrSize = end - begin + 1; head = begin; } // we want to shrink it from the beginning now // to make it the minimum size possible if (s[begin] in hash) { hash[s[begin]] += 1 // this is a character we need if (hash[s[begin]] > 0) { counter += 1; // make it invalid } } begin += 1;}This shrinks the window starting from the left to ensure we're only keeping the essential substring. We repeat this enlarging and then shrinking of the window, testing each one against our requirements.
This piece allows us to store the "best one" (by condition) found so far:
1if (end - begin + 1 < substrSize) { // overwrite if current substr is smaller
2 substrSize = end - begin + 1;
3 head = begin;
4}At the end, we simply use the tracked data to get the substring we want:
1if (substrSize == s.length + 1) {
2 return "";
3} else {
4 return s.slice(head, head + substrSize);
5}One Pager Cheat Sheet
- This lesson introduces the sliding windows algorithm pattern, which usually involves searching for a longest, shortest or optimal sequence that satisfies a given condition, and can be solved in
O(N)time andO(1)space complexity. - The
sliding windowof size 4 can be seen visually in theimageabove. - A sliding window can be used to find the
longest substringcontaining all characters in an ordered data structure. - The brute force approach to find if a string contains a certain set of characters runs in
O(N²)time, while utilizing a sliding window optimizes the process and provides a more efficient solution. - We need to grow and then shrink our
windowuntil we have avalid substringthat contains all the characters we are looking for. - The
sliding windowtechnique can be used to find the minimum substring containing all characters in a given set, as demonstrated by the hypothetical example“HGFDSAXZBJKC”. - The
Brute Forceapproach involves testing all possible substrings of length4against the entire string“HGFDSAXZBJKC”and checking if they contain all the necessary characters, with alternate substrings of greater lengths if not, resulting in a time complexity ofO(N²). - We can improve the performance of our solution by using the
sliding window techniqueto break the problem down. - We view a section of the array by using
beginandendpointersto create a "window". - We need a
counterthat checks the validity of our current substring and starts with the length of the required characters, decrementing as they get processed. - We
decrementthecounterwhen we encounter a required letter, and if it reaches0, we know the length is valid. - The tracker variables for our example of
"HGFDSAXZBJKC"and"ABKC"areLStart,LEnd,RStartandREnd. - We are testing the window by iterating through each letter to find a valid window, using a
counterto store the length of the substring and modifying ahashfor each letter requirement. - We
decrementourcountervariable andmodifythe dictionary to extend our window until wefindthe string that fulfills the problem's conditions, which is done bymoving the pointersandexpanding the scopeof the window. - We are updating the
hashmap to mark that the characterAhas been accounted for and adjusting thecounteraccordingly before stepping into checking the next letter. - We can shrink our window until we have a valid substring with all the required letters, but no unnecessary ones.
- We shrink and enlarge a window of characters in a string, keeping track of the
smallest substringthat satisfies certain conditions and thenreturning itat the end.


