AlgoDaily - How Does DP Work? Dynamic Programming Tutorial

Home > Data Structures and Algorithms 🚀 > Dynamic Programming Interview Questions > How Does DP Work? Dynamic Programming Tutorial

Objective: In this lesson, we'll cover this concept, and focus on these outcomes:

You'll learn what dynamic programming is.
We'll demystify it by showing you how to use this concept in programming interviews.
We'll walk through several examples applying the technique.

Out of all the possible interview topics out there, Dynamic Programming seems to strike the most fear in people's hearts. Dynamic Programming is somewhat unintuitive and there's an aura around it as something to be feared.

But there's no reason why it should be this way! Taking the time to properly understand these problems can make Dynamic Programming (DP) fun and easier to understand. Throughout this lesson, we'll cover a system to help solve most of these problems and to show that all dynamic programming problems are very similar.

Deep Dive into Dynamic Programming

If I were to ask you what the sum of these numbers are, you know the answer would be 6.

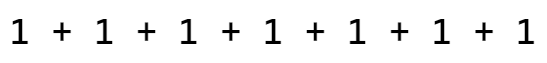
But let's say if I were to say add another 1 to the right of these digits. Then you'd also know what the answer is 7.

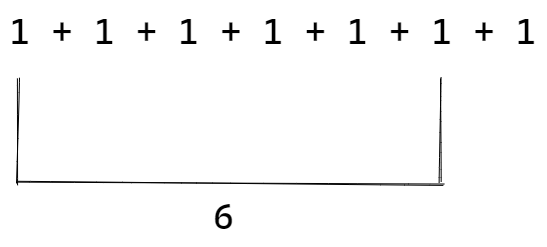
This may seem elementary. But the reason you didn't need to recount was that you remembered there were 6. This is the foundation of Dynamic Programming, remembering information to save time.

The Theory

Dynamic Programming is a method for solving a complex problem by breaking it down into a collection of simpler subproblems. These subproblems are solved just once and their solutions are stored using a memory-based data structure (via an array, hashmap, list, etc).

The solutions of a subproblem are typically stored and indexed in a specific way based on the values of its input parameters. This helps to facilitate its lookup.

What that means is that the next time the same subproblem occurs, instead of recomputing its solution, you simply just lookup the previously computed solution which saves computation time. This process of saving the solutions to the subproblems instead of recomputing them is called memoization.

Solving With the FAST Method

The FAST method consists of the following 4 steps:

Find the first solution
Analyze the solution
Identify the subproblems
Turn around the solution

Let's examine this process with the most popular example when it comes to dynamic programming, calculating the nth Fibonacci number:

xxxxxxxxxx
 
0, 1, 1, 2, 3, 5, 8, 13,..n

The nth Fibonacci number is where each number is the sum of the previous 2 numbers. If F(n) is the nth term of the series then we have F(n) = F(n-1) + F(n-2). For the sake of brevity, we won't go too much into the Mathematical proof. However, this is called a recursive formula or a recurrence relation. We need earlier numbers to have been computed before we can compute a later term.

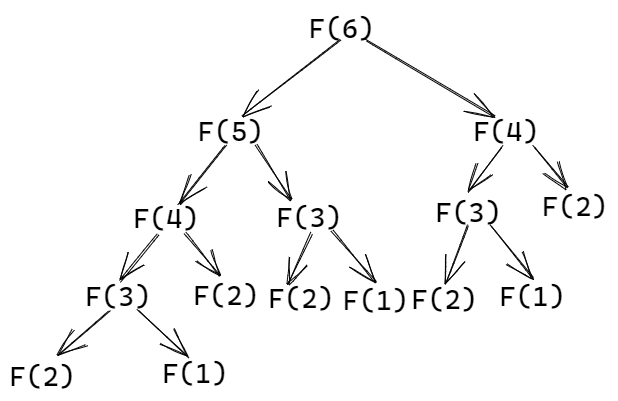
Finding the First Solution

The first step of the FAST method is taking a naive or brute force solution and making it dynamic. So we need to first find that brute force solution for the nth Fibonacci number.

This solution is not as efficient as it could be. But it won't matter right now since we're still going to optimize it.

xxxxxxxxxx
 
function fib(n) {
    if (n === 0) return 0;
    if (n === 1) return 1;
​
    return fib(n - 1) + fib(n - 2);
}

Analyze the solution

Next, we need to analyze the solution. If we look at the time complexity of our fib() function, we see that our solution will take 0(2^n). This is a very inefficient runtime.

If we want to optimize a solution using dynamic programming, it must have an optimal substructure and overlapping subproblems. We know it has overlapping subproblems because if you call fib(6), that will call fib(5) and fib(4).

fib(5) then recursively calls fib(4) and fib(3). From this, it's clear that fib(4) is being called multiple times during the execution of fib(5).

It also has an optimal substructure because we can get the right answer just by combining the result of the subproblems.

With these characteristics, we know we can use dynamic programming!

Identify the Subproblems

The subproblems are just the recursive calls of fib(n-1) and fib(n-2). We know that fib(n) is the nth Fibonacci number for any value of n so we have our subproblems.

With our subproblems defined, let's memoize the results. This means we're going to save the result of each subproblem as we compute it and then check before computing any value whether or not its already computed. However, this will only require tiny changes to our original solution.

xxxxxxxxxx
 
function fib(n) {
    if (n < 2) return n;
​
    // create cache and initialize it to -1
    let cache = new Array(n + 1).fill(-1);
​
    // fill initial values
    cache[0] = 0;
    cache[1] = 1;
    return fibHelper(n, cache);
}
​
function fibHelper(n, cache) {
    // if the value is in the cache return it
    if (cache[n] >= 0) return cache[n];
​
    // else compute the result and add it to the cache
    cache[n] = fibHelper(n - 1, cache) + fibHelper(n - 2, cache);
    return cache[n];
}
​
console.log("fib(5) =", fib(5));

In this solution, we are creating a cache or an array to store our solutions. If there is an already computed solution in the cache, then we would just return it else we compute the result and add it to the cache.

For example, if we are calculating fib(4), the subproblems are fib(3) and fib(2). These solutions are then stored in the cache. Then, when we are calculating fib(3), our program checks to see if fib(2) and fib(1) were already stored inside the cache. We would continue until we hit our base case when our value n is less than 2.

Our new solution only has to compute each value once, so it runs in O(n) time complexity and O(n) space complexity because of the cache.

Turn around the situation

The final step is to make our solution iterative. With the previous (top-down) solution, we started with n and then repeatedly broke it down into smaller and smaller values until we reached n == 0 and n == 1. Instead, we will start with the base case and work our way up.

xxxxxxxxxx
 
function fib(n) {
    if (n === 0) return 0;
​
    // initialize cache
    let cache = new Array(n + 1).fill(0);
    cache[1] = 1;
​
    // iteratively fill cache
    for (let i = 2; i <= n; i++) {
        cache[i] = cache[i - 1] + cache[i - 2];
    }
    return cache[n];
}
​
console.log(fib(5));

This process follows a bottom-up (iterative) solution. Since we are iterating through all of the numbers from 0 to n just once, our time complexity is O(n) and our space complexity will also be O(n). This is similar to our top-down solution just without the recursion. This solution is likely easier to understand and is more intuitive.

Are you sure you're getting this? Is this statement true or false?

All problems that can be solved using top-down approach can also be solved using bottom-up approach in dynamic programming.

Press true if you believe the statement is correct, or false otherwise.

Let's test your knowledge. Fill in the missing part by typing it in.

Solving a problem using the FAST method of dynamic programming always increases the ___ complexity of the algorithm.

Write the missing line below.

Solving Dynamic Programming problems--A more intuitive approach

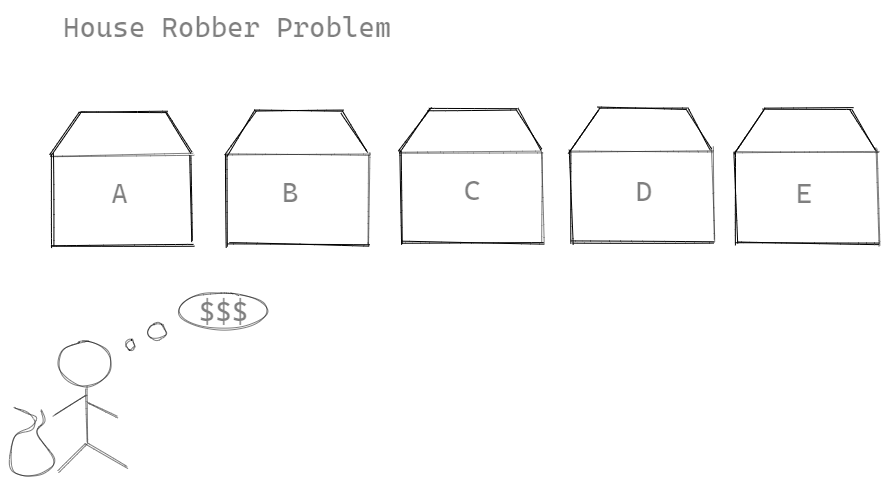
Another popular dynamic programming question is the House Robber problem.

The idea here is that robbers want to rob houses along a street and their only constraint is that they can't rob 2 adjacent houses. So what we need to do is to calculate the maximum amount of money that they can rob up to any point. Eventually, if they can propagate the max amount of money to rob at the i'th house and the i eventually becomes the last house then we can know the max amount of money we can get.

A good way to start thinking about this is to consider how much money can they make if they rob 0 houses? Obviously, the answer would be 0. We can slowly start thinking about how much money can be robbed from 1 house, 2 houses, 3 houses and so on. Eventually, that will give us n houses.

So back to the first case. If we rob 0 houses then we will make $0.

xxxxxxxxxx
 
function rob(nums) {
    let len = nums.length;
    if (len === 0) return 0;
    // ...
}

If we rob one house then, we would just take what that house has.

1if (len === 1) return nums[0];

But if we have 2 houses it becomes a little more interesting. But it's still pretty simple. If house A has more money, we rob house A. But if house B has more money we rob house B.

1if (len === 2) return Math.max(nums[0], nums[1]);

When we have 3 houses it becomes a little less intuitive and this is where the dynamic programming comes in. Particularly the bottom up(iterative) process. If we are searching for the nth answer, we can solve a smaller subproblem for the ith answer to solve for n.

xxxxxxxxxx
 
let arr = new Array(len);
arr[0] = nums[0];
arr[1] = Math.max(nums[0], nums[1]);
for (let i = 2; i < len; i++) {
    arr[i] = Math.max(arr[i - 2] + nums[i], arr[i - 1]);
}
return arr[arr.length - 1];

The code put together would look like:

xxxxxxxxxx
 
function rob(nums) {
    let len = nums.length;
​
    if (len === 0) return 0;
    if (len === 1) return nums[0];
    if (len === 2) return Math.max(nums[0], nums[1]);
​
    let arr = new Array(len);
    arr[0] = nums[0];
    arr[1] = Math.max(nums[0], nums[1]);
​
    for (let i = 2; i < len; i++) {
        arr[i] = Math.max(arr[i - 2] + nums[i], arr[i - 1]);
    }
​
    return arr[len - 1];
}
​
let arr = [4, 8, 0, 1];
console.log(rob(arr));

The idea behind this solution is to solve the problem for simpler cases to help solve the larger problem(bottom-up process). We created an array arr where arr[i] will represent the max amount of money we can rob up to and including the current house. Once we populate the array, we simply return the last entry which represents the max amount of money we can rob given the constraints.

Build your intuition. Is this statement true or false?

Dynamic programming can provide an optimal solution if and only if there is knowledge of previous and current states.

Press true if you believe the statement is correct, or false otherwise.

Conclusion

Dynamic Programming doesn't have to be scary. Following the FAST method can get you to an optimal solution as long as you can come up with an initial brute force solution. However, just knowing the theory isn't enough, to build confidence and proficiency in dynamic programming you must practice programming by doing.

Try this exercise. Could you figure out the right sequence for this list?

Order the steps for the following problem, solved using dynamic programming.

Given n friends, each one can remain single or can be paired up with some other friend. Each friend can be paired only once. Find out the total number of ways in which friends can remain single or can be paired up.

Press the below buttons in the order in which they should occur. Click on them again to un-select.

Options:

Initialize an array
Add base case
Fill array using recursive formula
Loop from 0...n

One Pager Cheat Sheet

This lesson will help you demystify and learn the skill of Dynamic Programming by walking through examples and providing a system to help solve most problems.
Dynamic Programming helps us save time by remembering information.
Using the FAST method can help us break down complex problems into smaller subproblems, such as calculating the nth Fibonacci number.
The Fibonacci sequence is a recursive formula where each number is the sum of the previous 2 numbers.
We need to find the brute force solution for the nth Fibonacci number as the first step of the FAST method before we can optimize it.
Our solution uses Dynamic Programming because it has both overlapping subproblems and an optimal substructure.
We identify the subproblems as fib(n-1) and fib(n-2) in order to memoize them and save results.
We are creating a cache to store already computed solutions and returning them if they exist, leading to a time complexity of O(n) and a space complexity of O(n).
We will iteratively build from the base case and work our way up to solve the problem.
The bottom-up solution has an O(n) time and space complexity, while being easier to understand and more intuitive than the top-down solution.
Dynamic programming is an algorithm that solves complex problems by breaking them down into smaller subproblems and combining the solutions to obtain the optimal results, and it can be done either via a top-down or bottom-up approach.
The FAST method of dynamic programming trades off the time complexity of the algorithm for increased space complexity by allocating additional space to store data, thereby reducing the amount of time required to solve the problem.
By using a bottom-up approach to consider how much money can be made robbing 0 to n houses, the House Robber problem can be solved to find the maximum amount of money that robbers can make.
We would rob only one house and take what it has.
If house A has more money, we rob house A; otherwise, we rob house B.
The bottom-up (iterative) process of dynamic programming can be utilized to solve for the nth answer by solving smaller subproblems for the ith answer.
The code put together would look like this.
The bottom-up approach of solving simpler cases and building an array arr to store the max amount of money we can rob up to and including the current house ultimately allows us to find the maximum amount of money that can be robbed.
Dynamic programming allows for problems to be broken down into smaller subproblems and solutions from these subproblems to be stored and used to solve the larger problem, allowing for solutions without the need for knowledge of previous and current states, such as calculating the maximum amount of money we can rob for each house.
With FAST and enough practice, Dynamic Programming can be used to reach an optimal solution.
Using dynamic programming, the problem can be solved by initializing an array, looping from 0 to n, adding the base case, and filling the array using the recursive formula.