Understanding Space Complexity

In this tutorial, we will introduce the concept of space complexity. In simple words, it is the amount of memory required to run a program, proportional to the input size that's fed in. For computing the space complexity, we ought to consider two factors:

1. Input space: Space used by input.
2. Auxiliary space: The additional space used by the algorithm, e.g., to hold temporary variables or the space used by the activation stack.

Representation of Space Complexity

Space complexity is generally represented using big O notation in terms of the size of the input. Big O is a convenient way to let us mathematically express how the space requirements of a program grow with the change in the size of the inputs. Here are a few examples:

• An algorithm that uses a single variable has a constant space complexity of O(1).
• A method that requires an array of n elements has a linear space complexity of O(n).
• Computations using a matrix of size m*n have a space complexity of O(m*n).
• If a k-dimensional array is used, where each dimension is n, then the algorithm has a space complexity of O(n^k).
• If you store an entire tree in a program and the tree has a branching factor b and depth n then the space complexity of the program/algorithm is exponential, i.e., O(b^n).

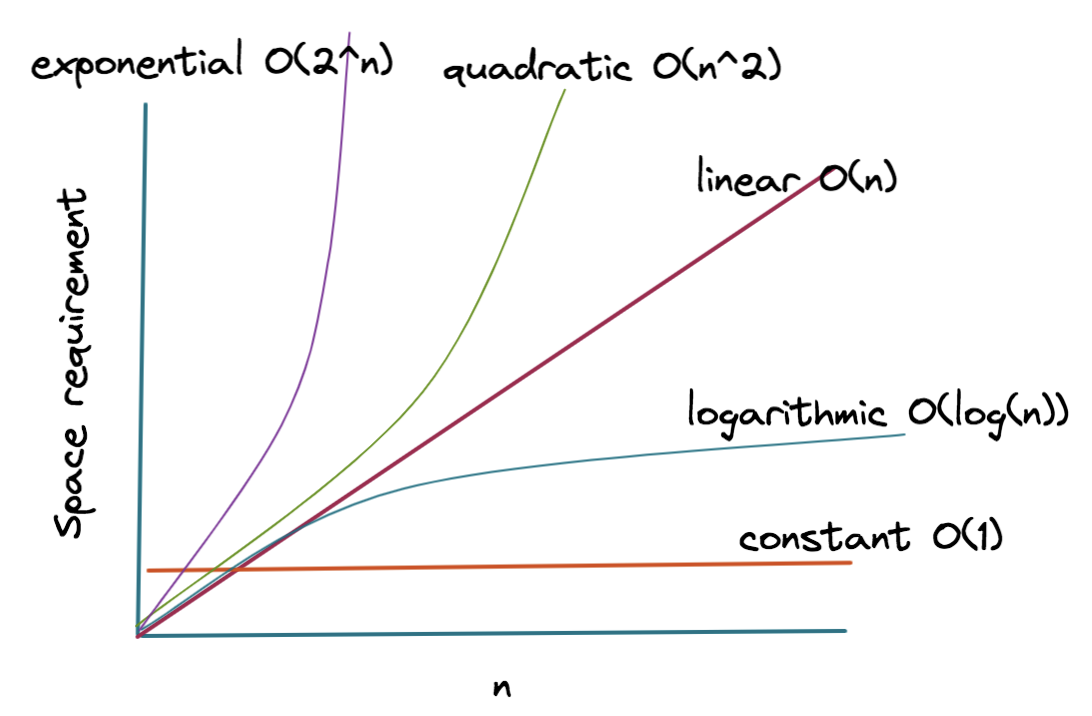
This way the complexity categorizes algorithms on the basis of their space requirements. The figure below shows the varying space requirements for different categories of space complexity.

Input vs Auxiliary Space

When analyzing space complexity, it helps to separate the memory into two buckets:

Space Type What It Counts Example Input space The memory used to store the given input The original array arr of length n Auxiliary space Extra memory the algorithm creates while running Temporary variables, helper arrays, recursion stack

This distinction matters because interviewers sometimes ask for overall space complexity, and sometimes they ask only for auxiliary space.

For example, if a function scans an input array and only uses sum and i, then:

1. Input space: O(n)
2. Auxiliary space: O(1)
3. Overall space complexity: O(n)

In many interview discussions, when someone says "space complexity," they often mean auxiliary space. If you're unsure, clarify which one they want.

Space used by recursive algorithms

The space used by recursive algorithms depends on the records being placed on the activation stack. The general rule is to count the maximum number of activation records on the stack at any given time.

If you generate a recursion tree of the program, then the space complexity would depend upon the total levels (depth) of the tree. You also carefully need to consider the variables being placed on the activation stack. An array being passed by reference to each recursive call would count as O(n). However, if the array is passed by value, then you need to take into account each copy of the array along with the maximum number of activation records in memory.

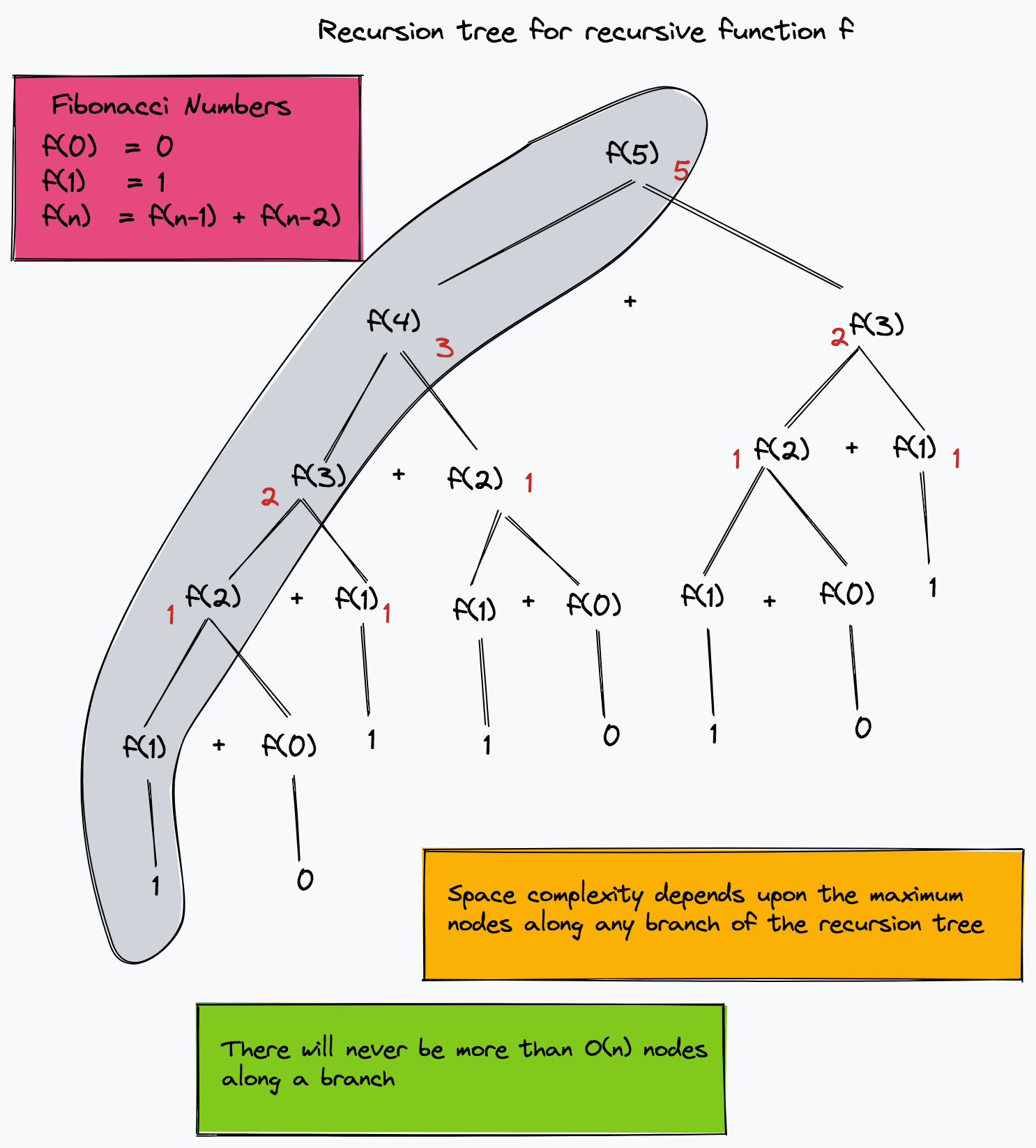
In the example below, the recursion tree for the recursive computation of Fibonacci numbers is shown. The figure shows that there won't be more than O(n) instances of the function f along any branch of the recursion tree at any given time. Hence the space complexity is O(n).

Choose the correct statement

Example 1: Factorial

Let's look at the classic problem of computing the factorial of a number. We'll discuss both the iterative case and the recursive solution.

Iterative Solution

The pseudo-code for the iterative solution is given below:

Function: factorial(n)
Returns:  Factorial of the number n

Method:
result = 1
for i = (1..n)
{
    result = result * i
}

return result

When we look at the factorial function, we can see that it uses the variable n, result and i. No matter how large the number n is, we always use these three variables to compute the factorial. Hence, the space complexity of this function is O(1). It means we can compute the factorial of any number in constant space.

Recursive Solution

The following is a recursive solution to computing the factorial: ```

Function: factorialRecursive(n) Returns: Factorial of the number n

Method: if n==0 return 1

result = factorialRecursive(n-1)*n return result

When we look at the recursive solution, we can see that there are n recursive calls to `factorialRecursive` function. Each call maintains a record on the activation stack. The stack holds a copy of the variables `n` and `result`. Hence, the space complexity of the recursive version of factorial is O(n).

What is the space complexity of the following algorithm?

Function: sumElements(arr)
Returns: Sum of all elements in array

Method:
n = length of arr
sum = 0

for i = (1 . . . n)
{
    sum += arr[i]
}
return sum

For recursive binary search, assume the array is passed by reference and no new sub-arrays are created.

Each recursive call only stores a few variables, but the maximum recursion depth is proportional to the number of times we can divide n by 2.

The auxiliary space complexity is ___.

Fill in the blank: _____________

Example 2: Binary Search

Let's take the example of binary search for finding a value in a sorted array. We'll look at both the iterative and recursive solution.

Iterative Solution

Function: binarySearch(arr, n, value)
Returns:  True/False

Method:
lower = 0
upper = n-1
found = false
while(lower<=upper and !found)
{
    mid = (lower+upper)/2
    if arr[mid] < value
        lower = mid+1
    else if arr[mid] > value
        upper = mid-1
    else
        found = true
}
return found

The space complexity of the iterative solution can easily be computed as follows: 1. Input space: O(n) 1. Auxiliary space with variables (n, value, lower, upper, found, mid): O(1) 1. Overall space complexity counting the input and auxiliary space: O(n)

Recursive Solution

Given below is the pseudo-code for the recursive version of binarySearch:

Function: binarySearchRecursive(arr, value, lower, upper)
Returns:  True/False
Call this function for array size n using: binarySearchRecursive(arr, value, 0, n-1)

Method:
if lower >= upper
    return false
mid = (lower+upper)/2
if arr[mid] == value
    return true
if arr[mid] < value
    return binarySearchRecursive(arr, value, mid+1, upper)

return binarySearchRecursive(arr, value, lower, mid-1)  

Here, the recursive calls generate the activation stack. Each record on the stack holds a separate copy of the variables lower, upper, mid and value. The array can be passed by reference so a separate copy of the array is not created for each function call. As we can have O(log(n)) calls to binarySearchRecursive function, the space complexity of the recursive version should include the O(log(n)) auxiliary space. Hence, the overall space complexity is:

1. Input space: O(n)
2. Auxiliary space for recursive calls involving O(log n) records created on stack: O(log n)
3. Overall space complexity counting the input and auxiliary space O(n)

Before moving on, separate the two questions interviewers often blend together:

• Auxiliary space: extra memory the algorithm creates while running.
• Total space: input space plus auxiliary space.

For factorial and binary search, the key difference is usually not the input—it is whether the solution builds a call stack.

Consider a problem where we have a graph with n nodes represented by an adjacency matrix.

Assuming we use a simple depth-first traversal for detecting a cycle in the graph, the space complexity will be ___.

Space Complexity of Various Sorting Algorithms

The input space for all sorting algorithms is at least O(n), where n is the size of the array. It is also important to understand the auxiliary space being used by that algorithm.

1. Bubble sort: The sorting is done in place and there is generally one extra variable used to store the temporary location for swapping successive items. Hence, the auxiliary space used is O(1).
2. Insertion sort: The case is the same as bubble sort. The sorting is done in place with a constant number of extra variables, so the auxiliary space used in O(1).
3. Merge sort: In merge sort, we split the array into two and merge the two sub-arrays by using a temporary array. The temporary array is the same size as the input array, hence, the auxiliary space required is O(n).
4. Heap sort: Heap sort is also implemented in place and hence the auxiliary space required is O(1).
5. Quick sort: Depending on how you implement quick sort, generally you would need O(log(n)) additional space to sort an array.

You can reduce space complexity for an algorithm by reducing the amount of computations in the algorithm.

Conclusions

Space complexity is an important aspect to consider when designing algorithms and implementing them. It gives the programmer a clear estimate of the memory requirements of the program before it is actually implemented. The choice of whether to use an iterative or recursive approach also affects the space complexity of the solution.

One Pager Cheat Sheet

• We will learn how to calculate space complexity by considering two main factors: Input space and Auxiliary space.
• Space complexity is generally represented using big O notation to express how the space requirements of a program grow with the change in the size of the inputs.
• - Separate input space from auxiliary space before giving the final space complexity.
• The space complexity of a recursive algorithm is dependent on the maximum number of activation records on the stack, as well as the variables being passed by reference or value.
• Recursion can require more memory than other algorithms, and stack overflow errors can occur without appropriate control due to activation records and copying of arguments for each call.
• The iterative solution of computing a factorial has a space complexity of O(1), while the recursive solution has a space complexity of O(n).
• The algorithm sumElements has a space complexity of O(n), since the number of iterations of the loop is equal to the size of the array.
• - Recursive binary search uses O(log n) auxiliary space because of the call stack.
• Binary search is a sorting algorithm used to find a value in an array with a space complexity of O(n) using either an iterative or recursive solution.
• - Iterative versions usually keep a few variables; recursive versions also pay for stack depth.
• The overall space complexity for a depth-first traversal to detect a cycle in a graph represented by an adjacency matrix with n nodes is O(n).
• The space complexity of sorting algorithms can range from O(1) to O(n) and is often dependent on the implementation.
• It is not possible to reduce the space complexity of an algorithm by reducing the number of computations, as the amount of memory needed is determined by the algorithm and the data structures used.
• Choosing between iterative or recursive approaches can greatly affect the space complexity of the algorithm, which should be a key consideration when designing and implementing programs.