Space used by recursive algorithms

The space used by recursive algorithms depends on the records being placed on the activation stack. The general rule is to count the maximum number of activation records on the stack at any given time.

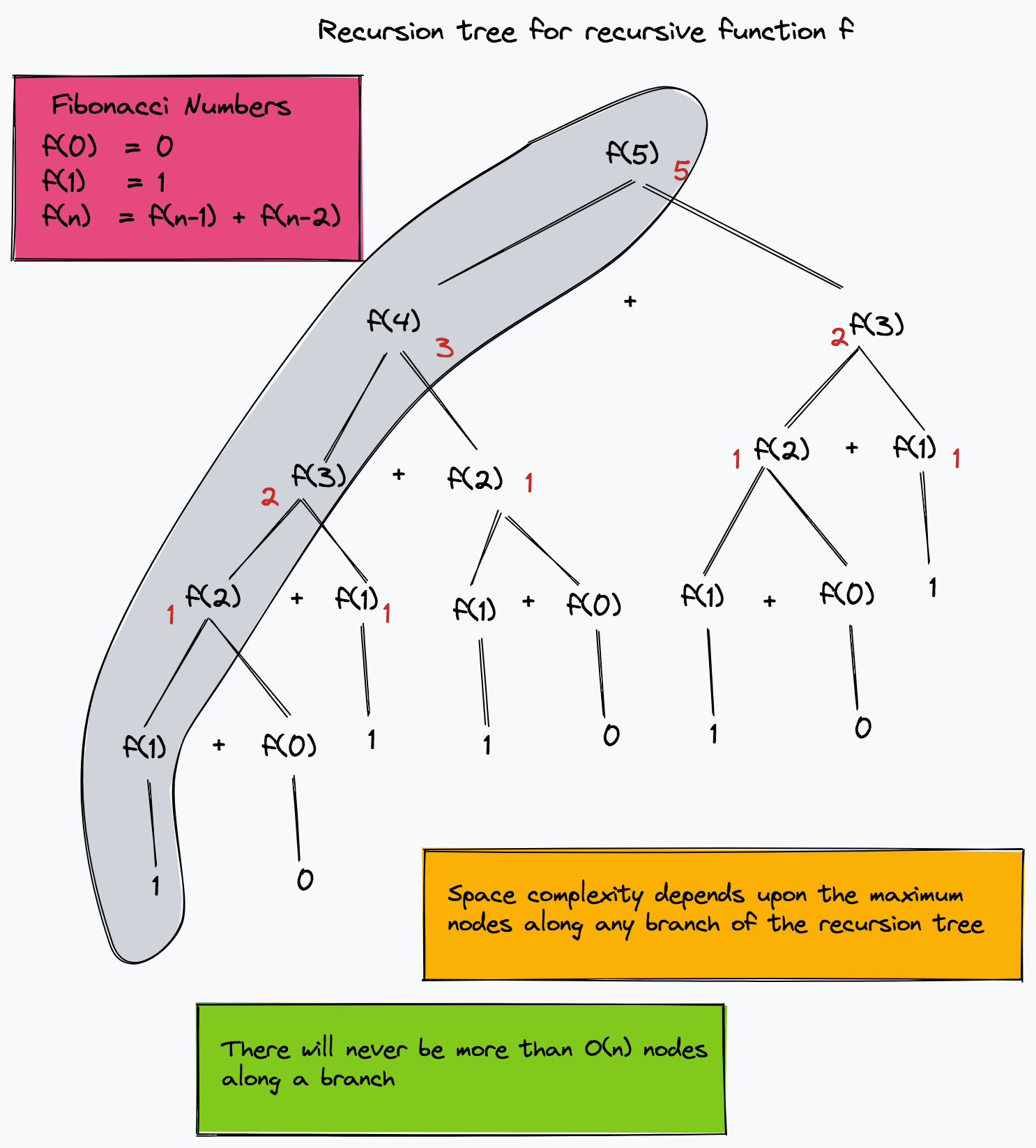
If you generate a recursion tree of the program, then the space complexity would depend upon the total levels (depth) of the tree. You also carefully need to consider the variables being placed on the activation stack. An array being passed by reference to each recursive call would count as O(n). However, if the array is passed by value, then you need to take into account each copy of the array along with the maximum number of activation records in memory.

In the example below, the recursion tree for the recursive computation of Fibonacci numbers is shown. The figure shows that there won't be more than O(n) instances of the function f along any branch of the recursion tree at any given time. Hence the space complexity is O(n).