AlgoDaily - Binary Tree Inorder Traversal

Good morning! Here's our prompt for today.

Can you write a function to traverse a binary tree in-order, and print out the value of each node as it passes?

SNIPPET

The example would output [4, 6, 5] since there is no left child for 4, and 6 is visited in-order before 5.

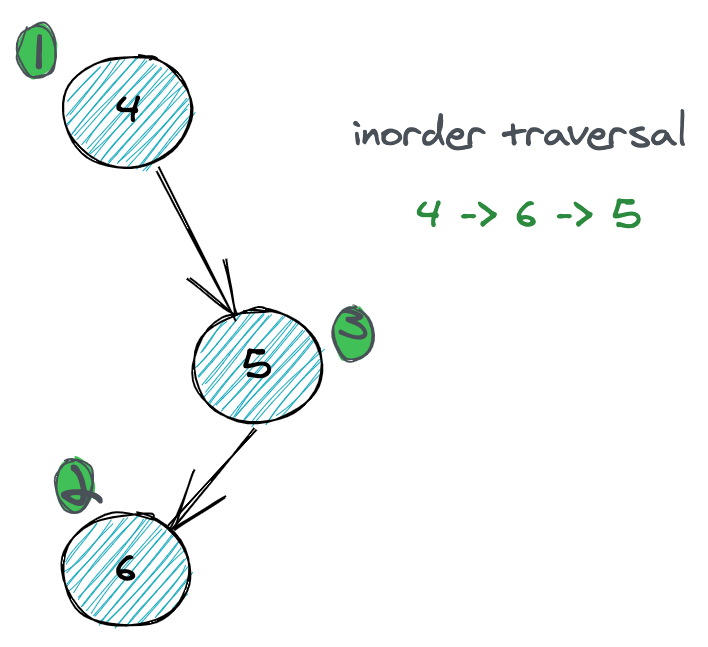
The definition of a tree node is as follows:

1public class Node {
2    int val;
3    Node left;
4    Node right;
5
6    public Node(int val) {
7        this.val = val;
8        this.left = null;
9        this.right = null;
10    }
11}

Follow up: you'll likely get the recursive solution first, could you do it iteratively?

Constraints

Number of vertices in the tree <= 100000
The values of the vertices in the tree will be between -1000000000 and 1000000000
Expected time complexity : O(n)
Expected space complexity : O(1)

Try to solve this here or in Interactive Mode.

How do I practice this challenge?

xxxxxxxxxx
​
 
import org.junit.Before;
import org.junit.Test;
import org.junit.runner.JUnitCore;
import org.junit.runner.Result;
import org.junit.runner.notification.Failure;
​
import static org.junit.jupiter.api.Assertions.assertIterableEquals;
​
import java.util.Arrays;
​
// solution
​
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
​
class Solution {
    public static List<Integer> inorderTraversal(Node root) {
        // fill in
        // with solution
        return new ArrayList<Integer>();
    }
​
    // print your findings using this function!
    public static void log() {
        System.out.println(inorderTraversal(null));
    }
}
​

Here's a video of us explaining the solution.

To change the speed of the video or see it in full screen, click the icons to the right of the progress bar.

Here's our guided, illustrated walk-through.

How do I use this guide?

This is one of those questions where knowing the terminology is necessary. In-order traversal visits the left child nodes first, then the root, followed by the right child (remember, it's called in-order because the current node's value is read in-between the left and right child nodes).

Recall the following ordering types:

Inorder traversal

First, visit all the nodes in the left subtree
Then the root node
Visit all the nodes in the right subtree

When to use? With a BST, the in order traversal will give the elements in ascending order, useful for problems where order matters.

SNIPPET

1// pseudo-logic of the inorder function:
2inorder(root.left)
3display(root.data)
4inorder(root.right)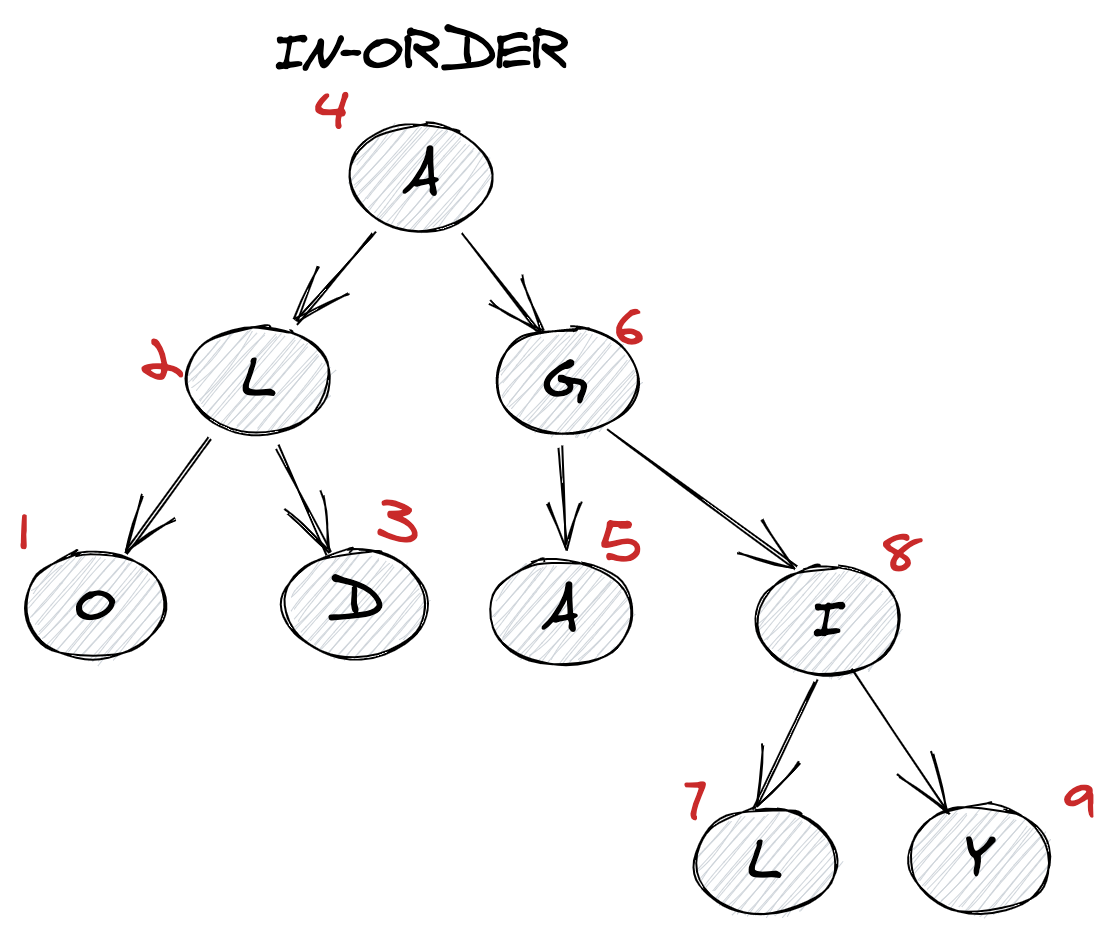

xxxxxxxxxx
}
 
import java.util.ArrayList;
import java.util.List;
​
public class Main {
    public static class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;
        TreeNode(int x) { val = x; }
    }
    
    private static void helper(TreeNode root, List<Integer> res) {
        if (root != null) {
            if (root.left != null) {
                helper(root.left, res);
            }
            res.add(root.val);
            if (root.right != null) {
                helper(root.right, res);
            }
        }
    }
​
    public static List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        helper(root, res);
        return res;
    }
​

Preorder traversal

Visit root node
Then go to all the nodes in the left subtree
Visit all the nodes in the right subtree

When to use? You can use pre-order traversal to create a copy of the tree, since you can access each node before its subtrees. It's also used to get expressions on an expression tree.

SNIPPET

1display(root.data)
2preorder(root.left)
3preorder(root.right)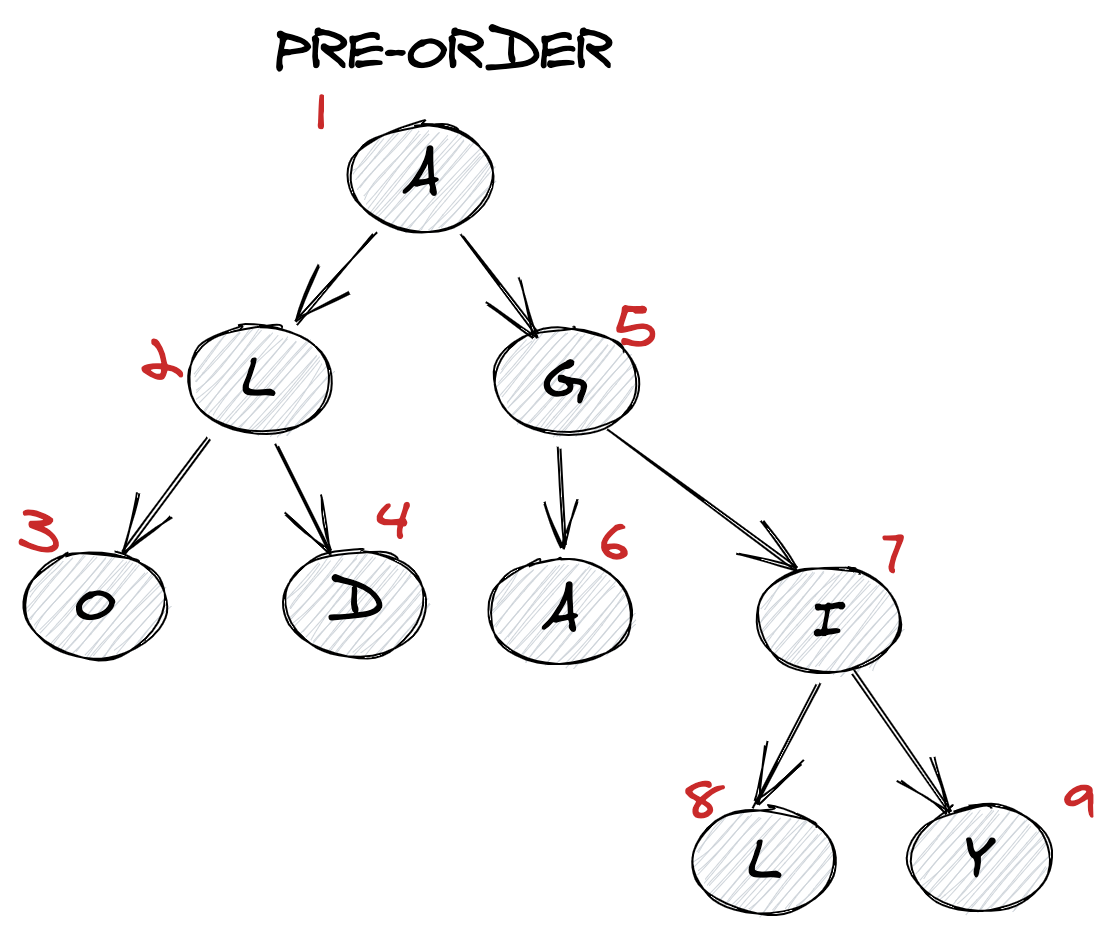

Note: This algorithm is equivalent to the famous graph algorithm Depth First Search (DFS).

xxxxxxxxxx
}
 
import java.util.ArrayList;
import java.util.List;
​
public class Main {
    public static class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;
        TreeNode(int x) { val = x; }
    }
    
    private static void helper(TreeNode root, List<Integer> res) {
        if (root == null) {
            return;
        }
        res.add(root.val);
        helper(root.left, res);
        helper(root.right, res);
    }
​
    public static List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        helper(root, res);
        return res;
    }
​
    public static void main(String[] args) {
        TreeNode root = new TreeNode(1);
        root.left = new TreeNode(2);

Postorder traversal

Visit all the nodes in the left subtree
Visit all the nodes in the right subtree
Visit the root node

When to use? You can use post-order traversal to delete a tree, since you can delete all of a node's children before itself.

SNIPPET

1postorder(root.left)
2postorder(root.right)
3display(root.data)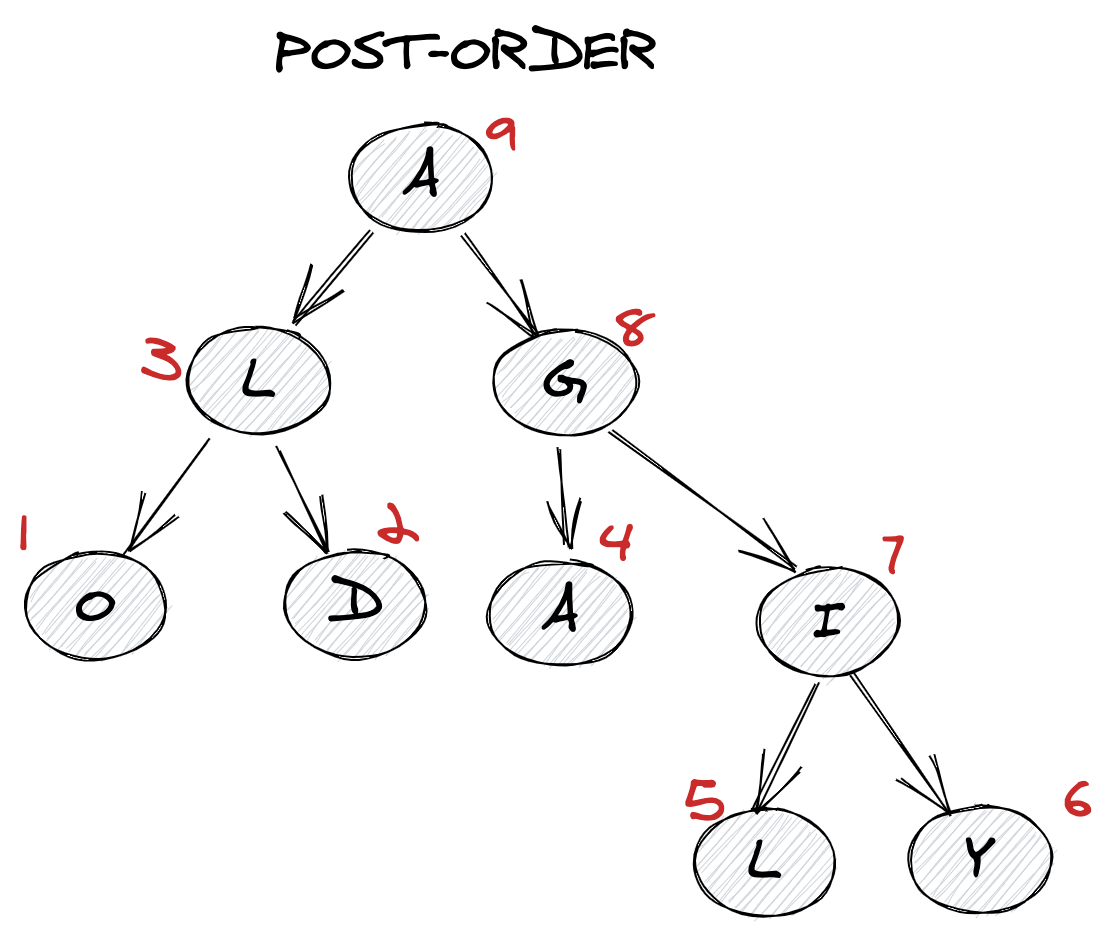

xxxxxxxxxx
}
 
import java.util.ArrayList;
import java.util.List;
​
public class Main {
    public static class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;
        TreeNode(int x) { val = x; }
    }
    
    private static List<Integer> res = new ArrayList<>();
    private static void helper(TreeNode root) {
        if (root == null) {
            return;
        }
        helper(root.left);
        helper(root.right);
        res.add(root.val);
    }
​
    public static List<Integer> postorderTraversal(TreeNode root) {
        helper(root);
        return res;
    }
​
    public static void main(String[] args) {
        TreeNode root = new TreeNode(1);
        root.left = new TreeNode(2);

Complexity Analysis

Worst case scenario time complexity is O(n). Where n is the number of nodes in the tree (in the worst case, we'd need to go through every node to find the value we want).

As this is the recursive solution, it will require memory in the stack for each call of the traversal functions. So on average (balanced binary tree), the space complexity is O(logn). And in the worst case (skewed binary tree), the space complexity will be O(n).

For more information on tree complexities, check out our Big O Notation Cheat Sheet.

Note: Will the space complexity be same if we use an iterative solution for the traversal? Tell us in the discussion!

One Pager Cheat Sheet

Write a function to traverse a binary tree in-order and print the value of each node while it passes, while meeting the specified complexity requirements.
In-order traversal visits the left child nodes first, followed by the root, and then the right child, and is useful for obtaining ascending sorted order inBSTs.
Preorder traversal can be used to create a copy of the tree or to get expressions from an expression tree (equivalent to Depth First Search (DFS)) by displaying the root's data and then traversing its left and right subtrees.
With post-order traversal, display(root.data) will be called after traversing both left and right subtrees of the root node, which is useful for certain operations like tree deletion.
The worst case time complexity for a recursive tree traversal is O(n), and the corresponding space complexity is on average O(logn) (balanced binary tree) and O(n) (skewed binary tree).

This is our final solution.

To visualize the solution and step through the below code, click Visualize the Solution on the right-side menu or the VISUALIZE button in Interactive Mode.

xxxxxxxxxx
}
 
import org.junit.Before;
import org.junit.Test;
import org.junit.runner.JUnitCore;
import org.junit.runner.Result;
import org.junit.runner.notification.Failure;
​
import static org.junit.jupiter.api.Assertions.assertIterableEquals;
​
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
​
class Solution {
​
    public static List<Integer> inorderTraversal(Node root) {
        List<Integer> res = new ArrayList<Integer>();
        inorderTraversalHelper(root, res);
        return res;
    }
​
    private static void inorderTraversalHelper(Node node, List<Integer> res) {
        if (node != null) {
            if (node.left != null) {
                inorderTraversalHelper(node.left, res);
            }
​
            res.add(node.val);
​
            if (node.right != null) {
                inorderTraversalHelper(node.right, res);
            }
        }

Got more time? Let's keep going.

If you had any problems with this tutorial, check out the main forum thread here.

Constraints

Try to solve this here or in Interactive Mode.

Here's a video of us explaining the solution.

Here's our guided, illustrated walk-through.

Complexity Analysis

One Pager Cheat Sheet

This is our final solution.

Got more time? Let's keep going.

Programming Categories

Popular Lessons