Good morning! Here's our prompt for today.

Let's implement a Binary Search Tree! Recall that a binary search tree, or a BST, is a binary tree that is ordered via these two properties:

1. The left sub-tree of a node has a value less than or equal to its parent node's value.
2. The right sub-tree of a node has a value greater than to its parent node's value.

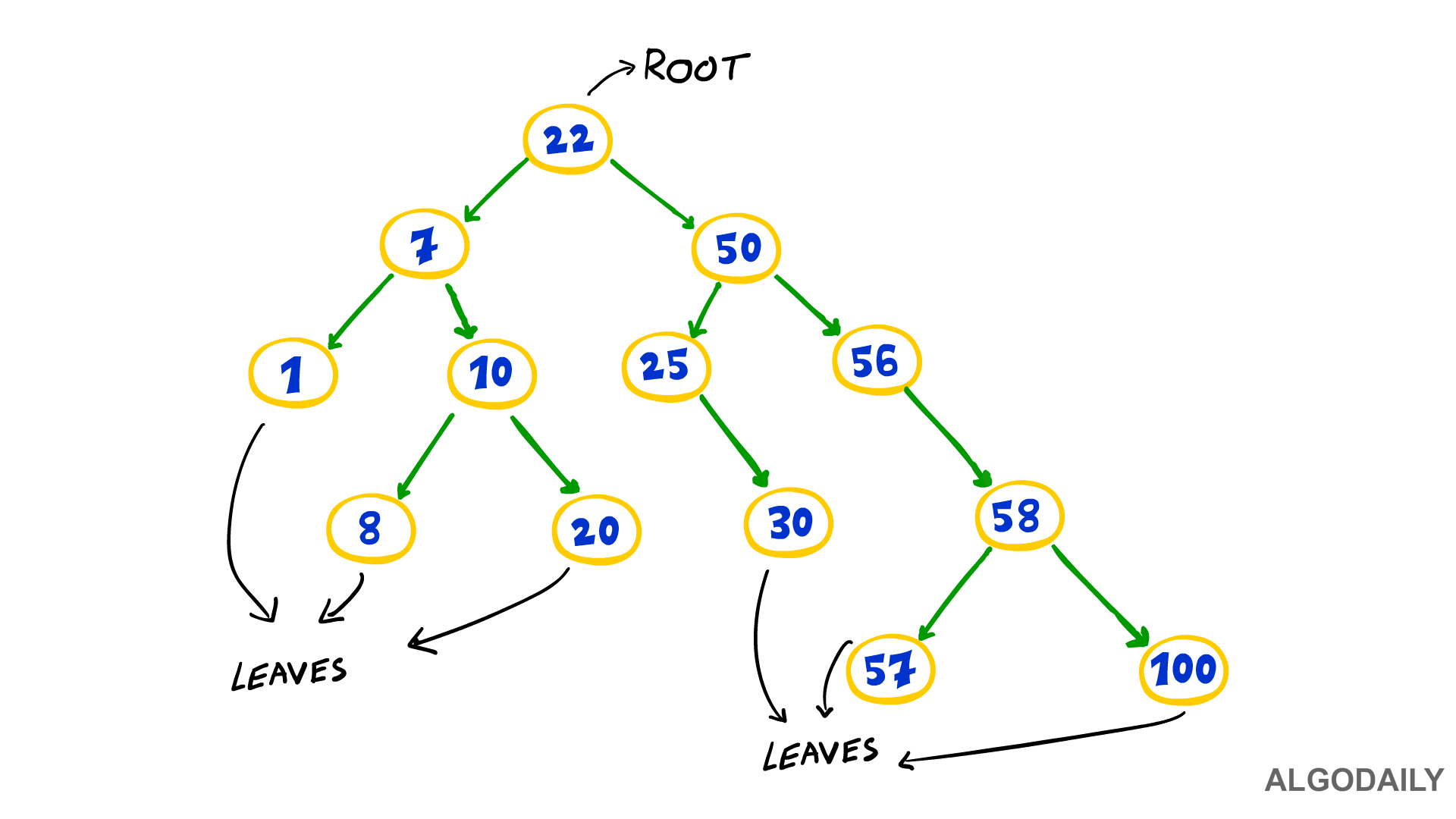
Given the following tree node definition:

1class Node {
2  constructor(val) {
3    this.val = val;
4    this.left = null;
5    this.right = null;
6  }
7}

Can you fill out the skeleton code and implement a binary search tree with #add and #remove methods?

1class BST {
2  constructor(val) {
3    this.root = new Node(val);
4  }
5
6  add(val) {
7    // fill this in
8  }
9
10  remove(val) {
11    // fill this in
12  }
13}

Constraints

• Maximum number of nodes <= 1000
• Value of each node can lie between -1000000000 and 1000000000
• Expected time complexity for most BST operations (including search, insert, and delete) is O(log n) where n being the number of nodes
• Expected space complexity : O(n)

Try to solve this here or in Interactive Mode.

How do I practice this challenge?

xxxxxxxxxx

​

class BST:

    def __init__(self, key):

        self.key = key

        self.left = None

        self.right = None

​

    def getMinimum(self, bst):

        return

​

    def add(self, node, val):

        return

​

    def remove(self, root, val):

        return

​

​

# Node definition

class Node:

    def __init__(self, val):

        self.val = val

        self.left = None

        self.right = None

​

​

# Regular binary trees

tree1 = Node(4)

tree1.left = Node(1)

tree1.right = Node(3)

​

Here's our guided, illustrated walk-through.

How do I use this guide?