Good morning! Here's our prompt for today.

Since a graph is one of the more difficult data structures to conceptualize in a programmatic 2D manner, let's go ahead and implement it! We'll go with an adjacency list version. Note that there's also the adjacency matrix method which we will cover later.

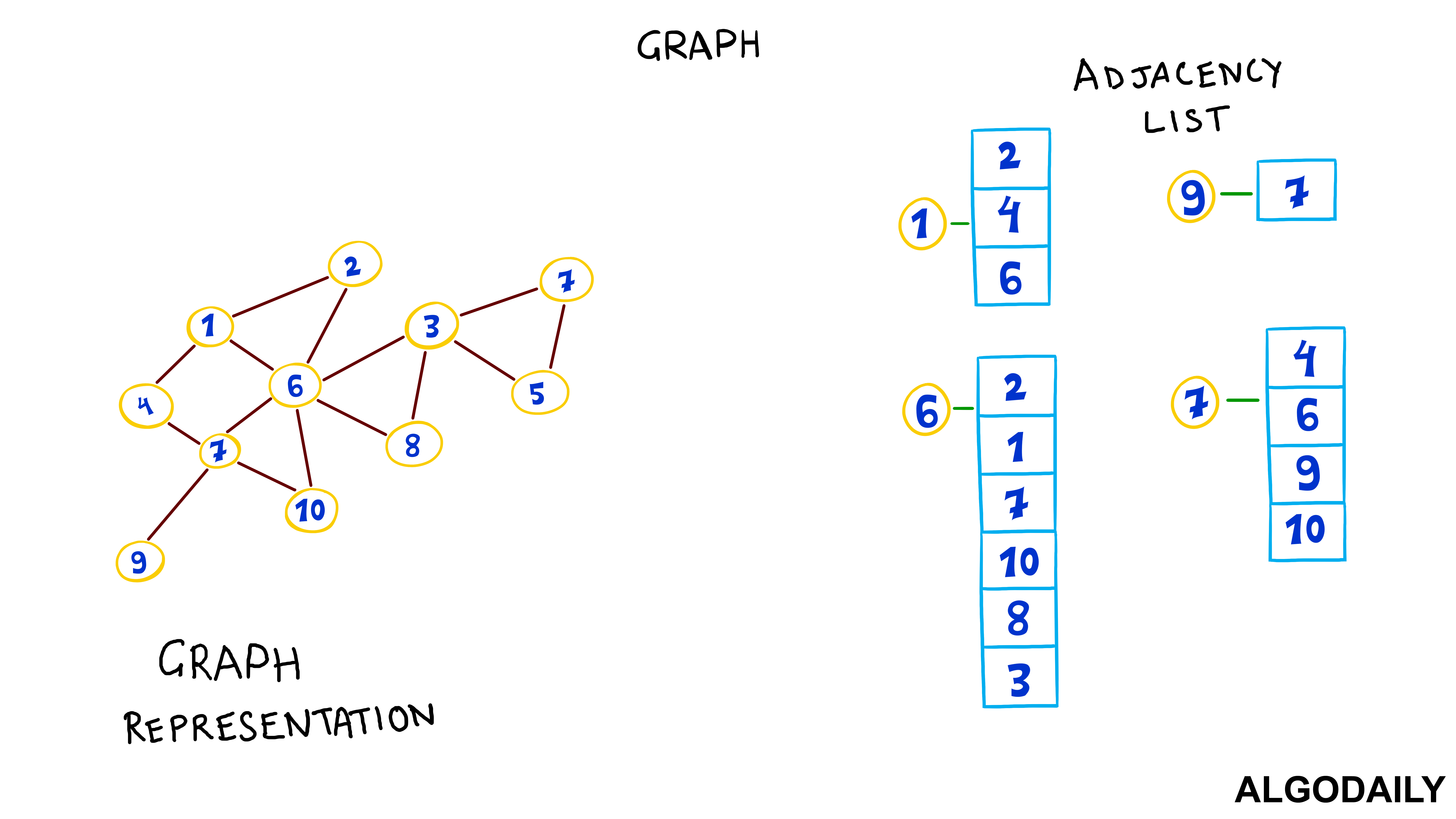
Recall that an adjacency list is a concept in graph theory, used to describe a representation of a graph via its nodes' adjacent (neighboring) nodes. You can think of it as each vertex maintaining a list of other vertices it's connected to. Using an unordered list data structure, each list is comprised of the node's neighbors.

Here's a skeleton of the implementation. Can you fill the rest in? What could be a good data structure to model this?

1class Graph {
2  constructor(verticesCount) {
3    this.adjacencyList = {};
4  }
5
6  addVertex(nodeVal) {}
7
8  addEdge(src, dest) {}
9
10  removeVertex(nodeVal) {}
11
12  removeEdge(src, dest) {}
13}

Constraints

• Number of nodes in the graph <= 100000
• It's advised to use a HashMap for the adjacency list
• Expected time complexity for all the utility functions is O(1)
• Expected space complexity is O(n)

Try to solve this here or in Interactive Mode.

How do I practice this challenge?

xxxxxxxxxx

​

class Graph:

    def __init__(self):

        self.adjacency_list = {}

​

    def add_vertex(node):

        # fill in this method

        return

​

    def add_edge(src, dest):

        # fill in this method

        return

​

    def remove_vertex(val):

        # fill in this method

        return

​

    def remove_edge(src, dest):

        # fill in this method

        return

​

​

import unittest

​

​

def checkEqual(L1, L2):

    return len(L1) == len(L2) and sorted(L1) == sorted(L2)

​

​

class Test(unittest.TestCase):

We'll now take you through what you need to know.

How do I use this guide?

Using a hash table, we're able to set each particular vertex as a hash key, and its value pairing to an array of adjacent vertices. We can use the default hash table data structure that comes with the language:

xxxxxxxxxx

class Graph {

  constructor() {

    this.adjacencyList = new Map();

    // we can iterate through keys with Map

    // and use objects and functions as keys

  }

The next step is to have methods that add and remove nodes to the graph by editing the adjacency lists.

To add a vertex, we can simply add a key to the hash table. The same with removal -- we'll just remove the key. However, with removal, there is the caveat that we also need to ensure that the node to be removed is also disregarded as a neighbor of other nodes.

In other words, if node A is a neighbor of B, and node A is to be removed, we should update B's adjacency list.

xxxxxxxxxx

addVertex(nodeVal) {

  this.adjacencyList.set(nodeVal, []);

  // set a key with the node value,

  // and an array to contain neighbors  

}

​

removeVertex(val) {

  if (this.adjacencyList.get(val)) {

    this.adjacencyList.delete(val);

  }

​

  this.adjacencyList.forEach((vertex) => {

    const neighborIdx = vertex.indexOf(val);

    if (neighborIdx >= 0) {

      vertex.splice(neighborIdx, 1);

    }

  })

}

Finally, we need to be able to add and remove edges (or connections) between the various nodes. Assuming this is a undirected graph, we can simply add the two nodes to each others' adjacency lists to create an edge:

xxxxxxxxxx

addEdge(src, dest) {

  this.adjacencyList.get(src).push(dest);

  this.adjacencyList.get(dest).push(src);

  // push to both adjacency lists   

}

Then, to remove an edge, let's do the inverse and splice them out of each others' lists.

xxxxxxxxxx

removeEdge(src, dest) {

  const srcDestIdx = this.adjacencyList.get(src).indexOf(dest);

  this.adjacencyList.get(src).splice(srcDestIdx, 1);

​

  const destSrcIdx = this.adjacencyList.get(dest).indexOf(src);

  this.adjacencyList.get(dest).splice(destSrcIdx, 1);

}

With those methods, we've built a simple graph class.