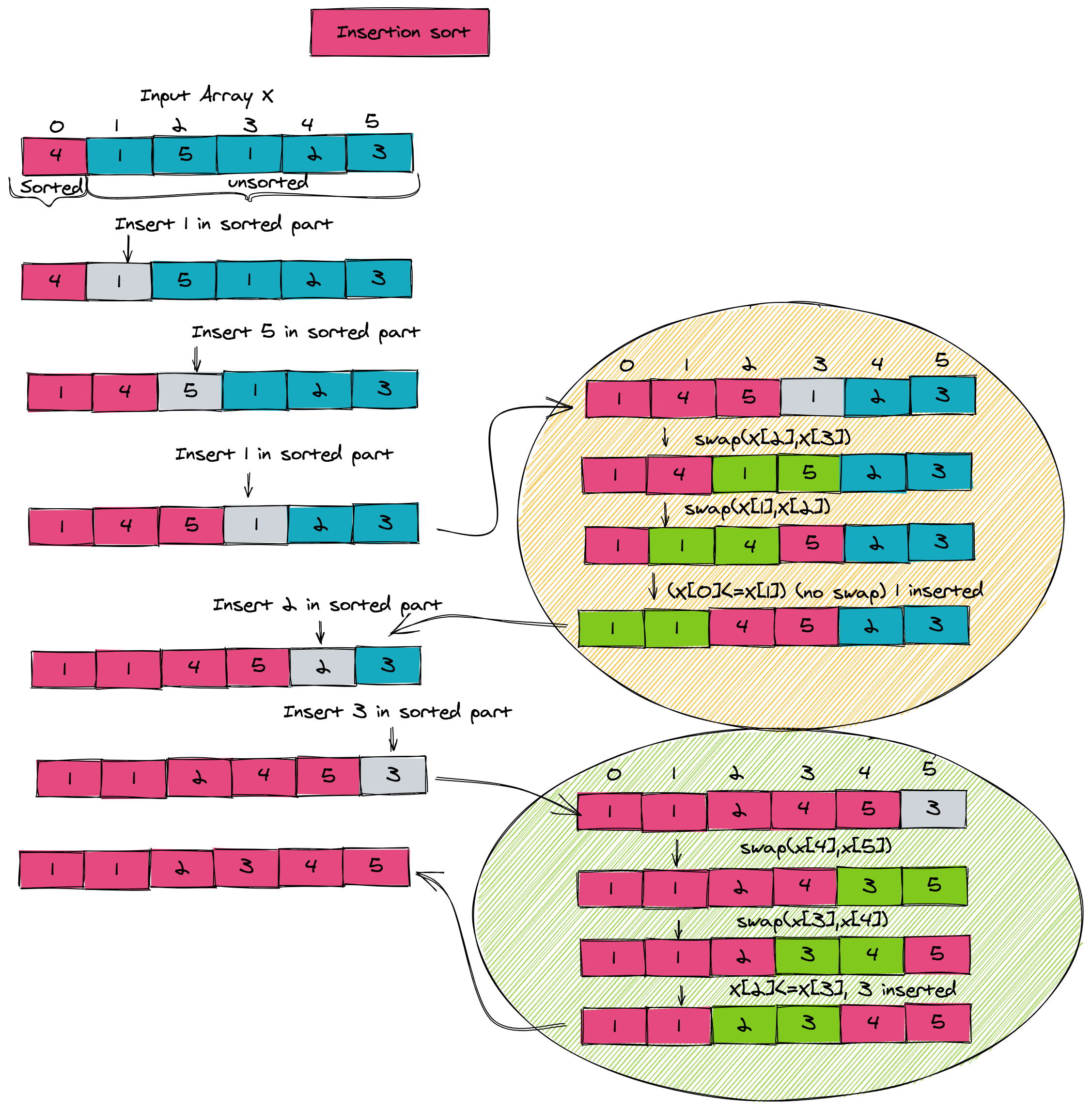
Again, what a marvelous piece of code! It's sorting an entire array in a simple manner. The outer loop represents a pass of the algorithm and the inner loop inserts one item from the unsorted part into the sorted part by successive comparisons. The whole process is illustrated in the figure below. Notice how the big bubbles illustrate the insertion process of the inner loop.
Complexity of Insertion Sort
Insertion sort, like bubble sort, has a time complexity that depends upon the input array.
We can see that if we input a sorted array, then insertion sort makes only one pass through the array, and thus its time complexity is O(n). However, in the worst-case scenario (say the input array is in descending order) then there are O(n) items to be inserted. Each insertion would make roughly O(n) comparisons, giving an overall quadratic time complexity-- O(n).
The sorting is in place and does not require any extra array memory making its space complexity O(1).


