How does this work in practical terms? Here's a gif of it being processed. Focus on how each "grouping" is grown as we iterate through the elements.

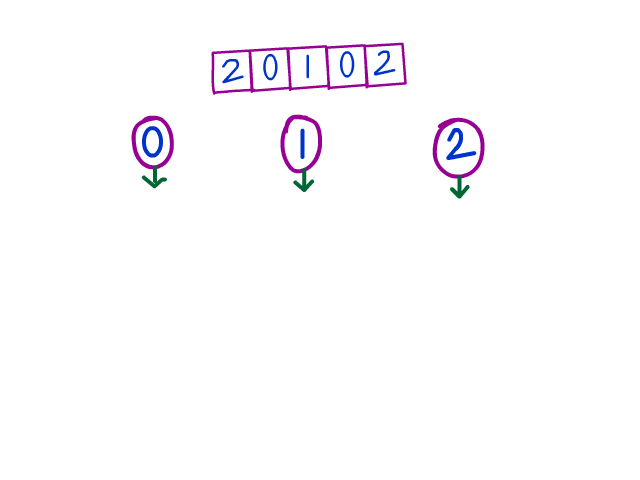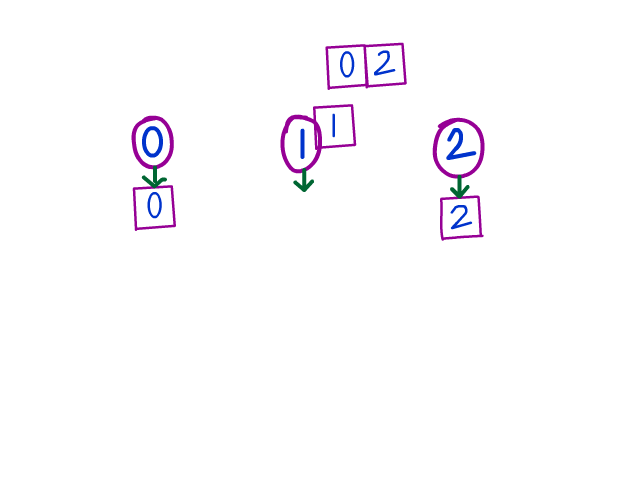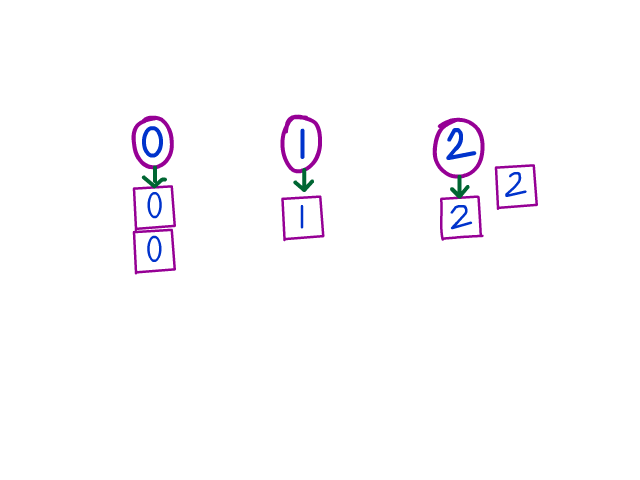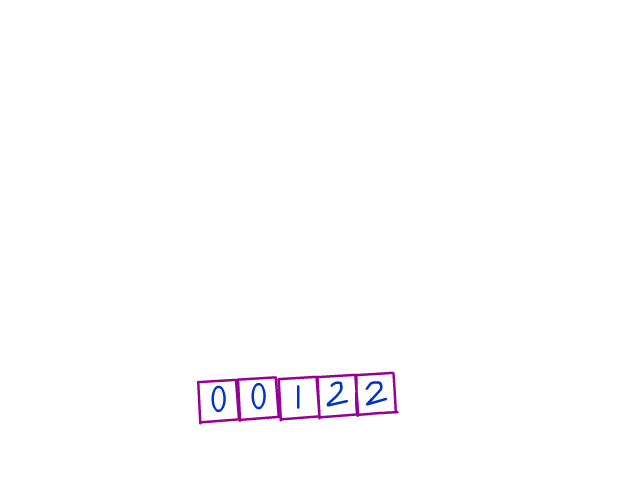
Here's another illustration that goes step by step. In this example, we start off with low and mid as 0, and high as (arr.length - 1), or 5 in this case. Really try to intuitively see the "growth" of each grouping.

Just as importantly, notice how the indices change over time, and try to see why they change.

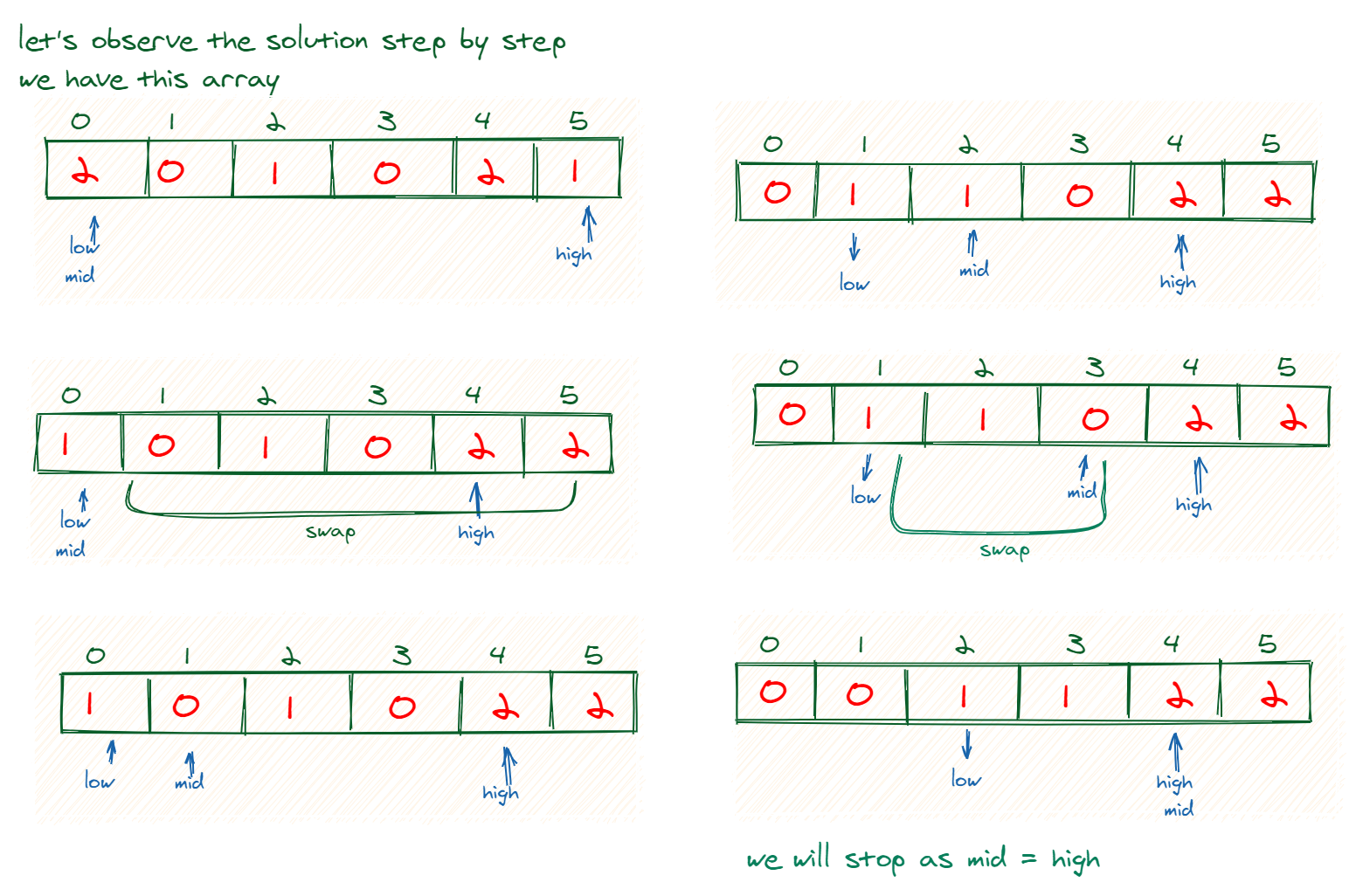
So what exactly are we doing? We start by analyzing the element just above the middle pointer, which is 0 at first. If that element belongs to the top group (2), swap it with the element just below the top.

Otherwise, if it belongs in the bottom group (0), swap it with the element just above the bottom. Finally, if it is a mid-group (1), we'll leave it where it is but update the index. These moves are, in a sense, "wiggling" it to the right place via swaps.

Let us now analyze the complexity of this solution. Think about how many times we need to go through the array in the worst case. As we can see, we will only move mid to right and high to left. So they will go linearly and collide with each other, resulting in the finishing point of the algorithm. So the complexity of the whole algorithm is linear O(n). Here n is the length of the given array.

We are swapping the elements of the array in-place. And, we are not allocating any new memory except some variables. So the space complexity would be constant O(1).