Good afternoon! Here's our prompt for today.
This problem is named the "Dutch national flag problem" because the flag of the Netherlands is comprised of the colors red, white, and blue in separate parts. Although we won't be using colors, the premise of the challenge is to develop a sorting algorithm that performs some form of separations of three kinds of elements.
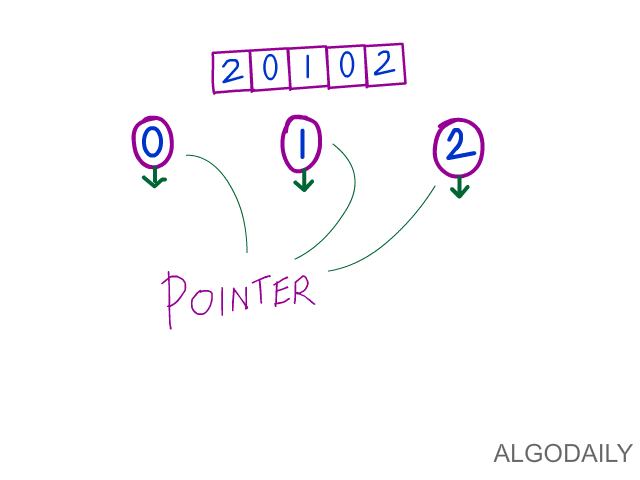
To simplify things, we'll use 0s, 1s, and 2s.
Given an array consisting of only 0s, 1s, and 2s, sort the elements in linear time and constant space.
1const arr = [2, 0, 1, 0, 2]
2dutchNatFlag(arr)
3// [0, 0, 1, 2, 2]Constraints
- Length of the array <=
100000
Try to solve this here or in Interactive Mode.
How do I practice this challenge?
xxxxxxxxxxdef dutch_national_flag(arr): # fill in return arrimport unittestclass Test(unittest.TestCase): def test_1(self): assert dutch_national_flag([2, 0, 1, 0, 2]) == [0, 0, 1, 2, 2] print("PASSED: assert dutch_national_flag([2, 0, 1, 0, 2]) == [0, 0, 1, 2, 2]") def test_2(self): assert dutch_national_flag([0, 1, 2]) == [0, 1, 2] print("PASSED: assert dutch_national_flag([0, 1, 2]) == [0, 1, 2]") def test_3(self): assert dutch_national_flag([2, 0, 0, 1, 1, 0, 2, 2]) == [0, 0, 0, 1, 1, 2, 2, 2] print( "PASSED: assert dutch_national_flag([2, 0, 0, 1, 1, 0, 2, 2]) == [0, 0, 0, 1, 1, 2, 2, 2]" )if __name__ == "__main__": unittest.main(verbosity=2) print("Nice job, 3/3 tests passed!")We'll now take you through what you need to know.
How do I use this guide?
Try this exercise. Is this statement true or false?
Before we proceed, let's check your understanding of sorting algorithms.
The recurrence and time complexity for worst case of the QuickSort algorithm is T(n-1) + O(n) and O(n^2) respectively.
Press true if you believe the statement is correct, or false otherwise.
Are you sure you're getting this? Could you figure out the right sequence for this list?
What is the order of steps in Quick Sort?
Press the below buttons in the order in which they should occur. Click on them again to un-select.
Options:
- Then, apply the quicksort algorithm to the first and the third part. (recursively)
- Pick a pivot element.
- Partition the array into 3 parts: all elements in this part is less than the pivot, the pivot, and all elements greater.
This problem is a variant of the quick sort algorithm, so we know we'll need to do some form of partitioning. Partitioning is the act of splitting an array up into sub-arrays, "according to whether they are less than or greater than" a pivot number.
At first glance, it seems like an impossible task: how can we determine where an element should go without being aware of its relative positioning compared with the rest of the elements?
There's one way-- by using multiple pointers.
The idea behind the final dutch national flag algorithm is to use three pointers, low, mid, and high. We start with low and mid initialized to 0, and our goal is to expand these "groups" (the sub-array from one of these indices to the next) over time. We'll do this via a series of swaps.
Don't worry, we'll break this down more as we go.
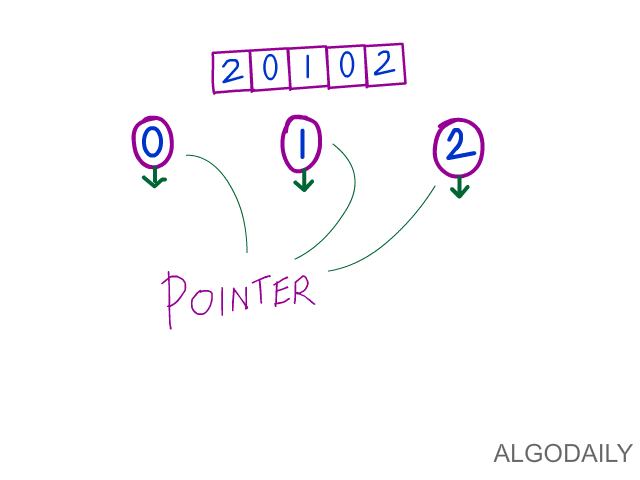
As mentioned, we'll be doing some swapping once the partitions are properly arranged. At a high level, using this strategy, we'll start with three groups:
- Index
0tolow- this is the "bottom group" - Index
lowtomid- this is the "middle group" - Index
midtohigh- this is the "top group"
The idea is to set these initial groups, and then have the top "grow downwards" -- meaning to swap and properly assign the elements in each group, from top to bottom. So we'll see a line like this get executed:
1swap(arr, mid, high--);Same with the bottom, except reverse, the bottom will grow bottom-up:
1swap(arr, low++, mid++);And what about the middle?
The middle needs to stay above the bottom. Please find the code attached to see the core conditional logic put together.

xxxxxxxxxxif (arr[mid] === 0) { swap(arr, low++, mid++);} else if (arr[mid] === 2) { swap(arr, mid, high--);} else if (arr[mid] === 1) { mid++;}How does this work in practical terms? Here's a gif of it being processed. Focus on how each "grouping" is grown as we iterate through the elements.
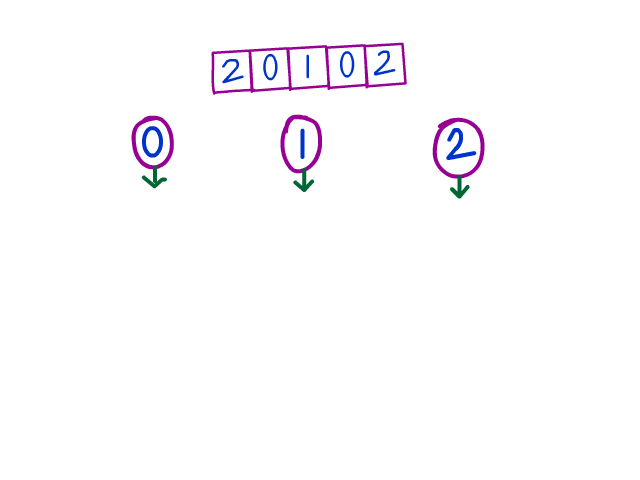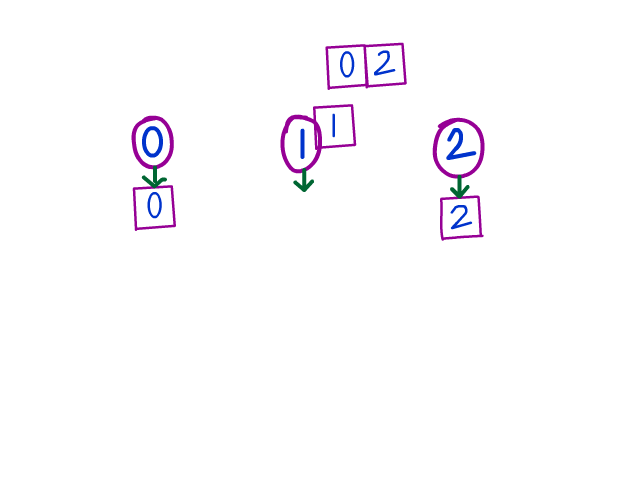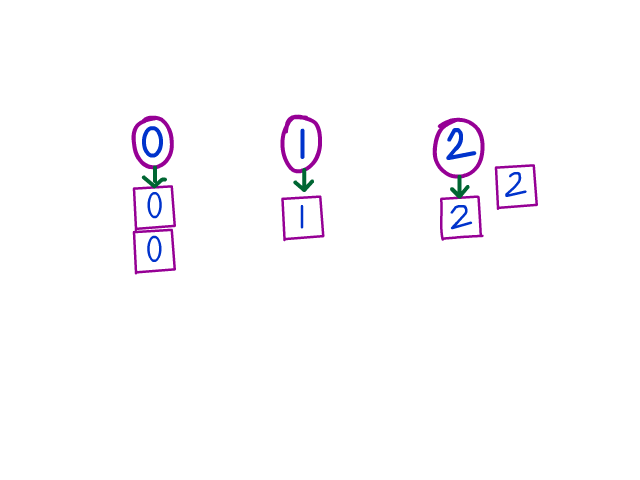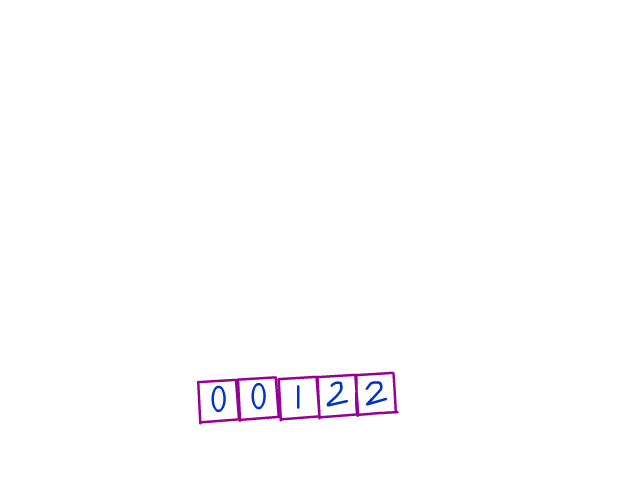
Here's another illustration that goes step by step. In this example, we start off with low and mid as 0, and high as (arr.length - 1), or 5 in this case. Really try to intuitively see the "growth" of each grouping.
Just as importantly, notice how the indices change over time, and try to see why they change.
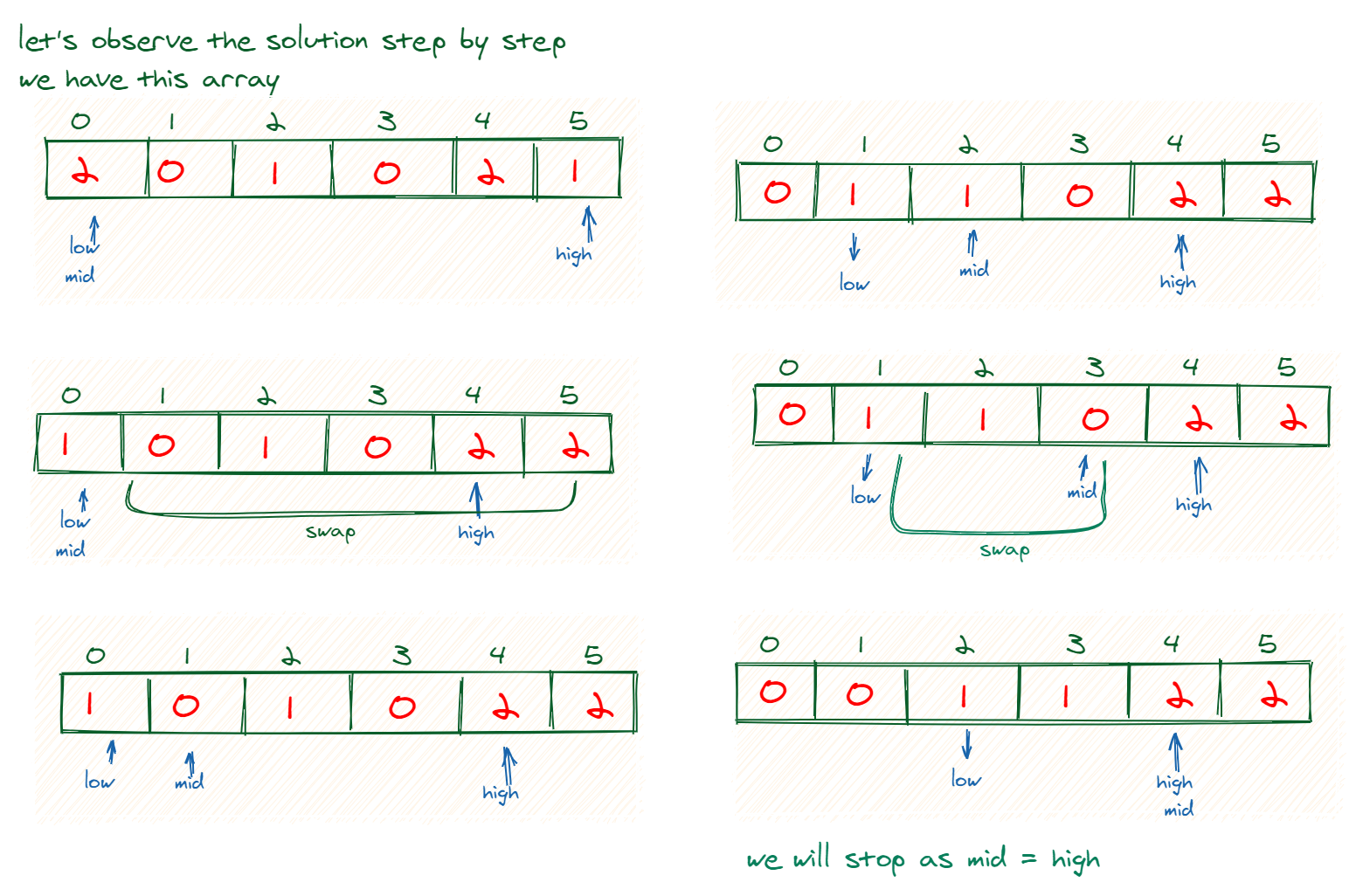
So what exactly are we doing? We start by analyzing the element just above the middle pointer, which is 0 at first. If that element belongs to the top group (2), swap it with the element just below the top.

Otherwise, if it belongs in the bottom group (0), swap it with the element just above the bottom. Finally, if it is a mid-group (1), we'll leave it where it is but update the index. These moves are, in a sense, "wiggling" it to the right place via swaps.

Let us now analyze the complexity of this solution. Think about how many times we need to go through the array in the worst case. As we can see, we will only move mid to right and high to left. So they will go linearly and collide with each other, resulting in the finishing point of the algorithm. So the complexity of the whole algorithm is linear O(n). Here n is the length of the given array.
We are swapping the elements of the array in-place. And, we are not allocating any new memory except some variables. So the space complexity would be constant O(1).
Let's test your knowledge. Click the correct answer from the options.
How many pointers are necessary for the dutch national flag problem?
Click the option that best answers the question.
- 1
- 2
- 3
- None
Try this exercise. Could you figure out the right sequence for this list?
Dutch Nation Flag algorithm
Press the below buttons in the order in which they should occur. Click on them again to un-select.
Options:
- If arr[mid] == 2, then swap arr[mid] and arr[high] and decrease `high` by 1
- Initialize a `low` variable pointing to the start of the array and a `high` pointing at the end
- Declare a `mid` pointer that iterates through each element starting at index 0
- If arr[mid] == 0, then swap arr[mid] and arr[low] and increase `low` and `mid` by 1
- If arr[mid] == 1, don't swap anything and just increase the mid pointer by 1
We can also use bucket sorting in this problem. In bucket sorting, there must be a limited number of known elements in the array. This is exactly the case in this problem. We only have 3 values (0, 1, and 2).
So to apply bucket sort, we create a list of buckets (counts) and count all the elements in the array to their corresponding buckets. Then, we do the in-place placement of the number of elements in the array and return it. See the solution code below. This is actually simpler than quicksort, as we do not need to keep track of three pointers.
Similar to the algorithm above, we are just passing through the array twice only. So the complexity of the below code will also be O(2n) = O(n). Again, we are only allocating a number of variables. Keep in mind that counts array is a very small fixed-sized (3) array. So it won't make the memory complexity linear. The space complexity of this algorithm would be O(1).
xxxxxxxxxxdef dutch_national_flag(arr): counts = [0, 0, 0] for i in arr: counts[i] += 1 i = 0 for val, count in enumerate(counts): for _ in range(count): arr[i] = val i += 1 return arrOne Pager Cheat Sheet
- The Dutch national flag problem requires sorting an array consisting of only
0s,1s, and2s in linear time and constant space. - The time complexity for the worst case of the QuickSort algorithm is O(n^2) because it often chooses the last element as the pivot and keeps partitioning the same subarrays.
- Quick Sort is a divide-and-conquer algorithm which divides an array into three parts, recursively partitions them, and finally sorts the array in ascending order.
- The Dutch National Flag Problem is solved by using multiple pointers to expand "groups" over time by a series of swaps.
- We will swap elements in a given array with indices split into three "groups" to arrange the partitions, having the top group "grow downwards" and the bottom group "grow upwards".
- The
Dutch National Flag Problemrequires the middle to stayabove the bottom, with its core conditionallogicto be put together. - We are swapping elements in-place and analyzing them with respect to the
low,mid, andhighindices to sort them into specific groupings, resulting in linearO(n)time complexity and constantO(1)space complexity. - The Dutch National Flag Problem is solved by establishing three
pointers--low,mid, andhigh-- and using them to iterate through the array and swap elements to "wiggle" them to the right place. - The Dutch National Flag algorithm uses one pointer and three boundary variables -
low,mid, andhigh- to sort an array of 0, 1, 2 elements in linear time. - We can apply bucket sorting with
O(n)complexity andO(1)space complexity to solve this problem which uses 3 known elements (0,1, and2).
This is our final solution.
To visualize the solution and step through the below code, click Visualize the Solution on the right-side menu or the VISUALIZE button in Interactive Mode.
xxxxxxxxxx print("Nice job, 3/3 tests passed!")def swap(arr, i, j): temp = arr[i] arr[i] = arr[j] arr[j] = tempdef dutch_national_flag(arr): low = 0 mid = 0 high = len(arr) - 1 while mid <= high: if arr[mid] == 0: swap(arr, low, mid) low += 1 mid += 1 elif arr[mid] == 2: swap(arr, mid, high) high -= 1 elif arr[mid] == 1: mid += 1 return arrimport unittestclass Test(unittest.TestCase): def test_1(self): assert dutch_national_flag([2, 0, 1, 0, 2]) == [0, 0, 1, 2, 2] print("PASSED: assert dutch_national_flag([2, 0, 1, 0, 2]) == [0, 0, 1, 2, 2]")You're doing a wonderful job. Keep going!
If you had any problems with this tutorial, check out the main forum thread here.


