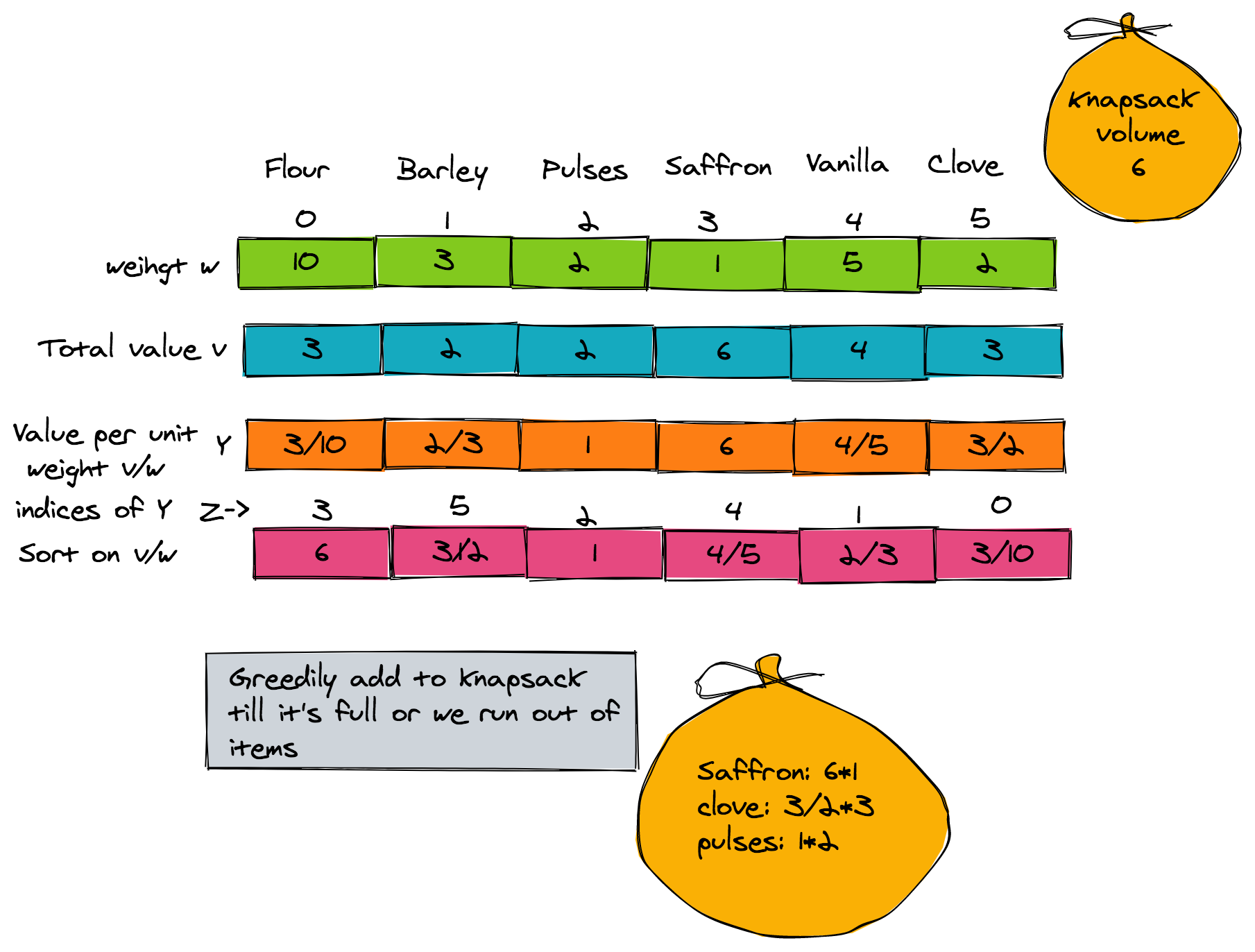
Greedy Solution of Fractional Knapsack Problem
There is an amazing method of solving the fractional knapsack problem which uses a greedy strategy. This greedy algorithm first computes the value per unit weight of every item (i.e. v/w). It then sorts v/w in descending order. After that comes the stage for filling the sack greedily-- by adding items in order of decreasing v/w values.
The pseudo-code of the solution is attached here.
Complexity of Fractional Knapsack Problem
In the pseudo-code we can see that step 8 scans each item only once, with O(n) running time. However, step 3 involves sorting, which has a running time complexity of O(n log n). Thus, the overall time complexity is O(n log n) and space complexity is also O(n). This is because we are using one additional array for storing v/w and another one for keeping the sorted indices.
1Routine: solveKnapsack
2Input: Weight array w, value array v of size n,
3 X = capacity of knapsack
4Output: Array R containing indices of items in the sack and
5 array Rwt that has the corresponding weight of
6 each item in the sack,
7 val: total value of items in sack,
8 RInd: total items added in sack
9
101. Initialize array R to -1 and array Rval to zero
112. Create an array Y containing value of each item per unit of weight
12 Y[i] = v[i]/w[i] for i = 0..(n-1)
133. Create an array Z, which has indices of the sorted values of Y in descending order.
144. remaining = X
155. i = 0
166. val = 0
177. RInd = 0
188. while (i < n and remaining < X)
19 a. toadd = min(remaining, w[Z[i]])
20 b. R[RInd] = Z[i]
21 c. Rwt[RInd] = toadd
22 d. val = val + val[Z[i]] * toadd
23 e. remaining = remaining - toadd
24 f. i = i+1
25 g. RInd = RInd + 1
269. return R, Rwt, val, RIndxxxxxxxxxxpublic class Knapsack{ public (List<int> R, List<int> Rwt, float val, int RInd) SolveKnapsack(List<int> w, List<float> v, int X) { int n = w.Count; List<int> R = new List<int>(new int[n]); List<float> vPerW = new List<float>(new float[n]); for (int i = 0; i < n; i++) vPerW[i] = v[i] / w[i]; List<int> idx = Enumerable.Range(0, vPerW.Count()).ToList(); idx.Sort((i, j) => vPerW[i].CompareTo(vPerW[j])); idx.Reverse(); int remaining = X, i = 0, RInd = 0; float val = 0; while (i < n && remaining < X) { int toAdd = Math.Min(remaining, w[idx[i]]); R[RInd] = idx[i]; val += v[idx[i]] * toAdd; remaining -= toAdd; i++; RInd++; } return (R, w, val, RInd); }}

