Greedy Algorithm for Maximizing Reward

The greedy algorithm for maximizing reward in a path starts simply-- with us taking a step in a direction which maximizes reward. It doesn't keep track of any other path. The algorithm only follows a specific direction, which is the local best direction. The pseudo-code for the algorithm is provided here.

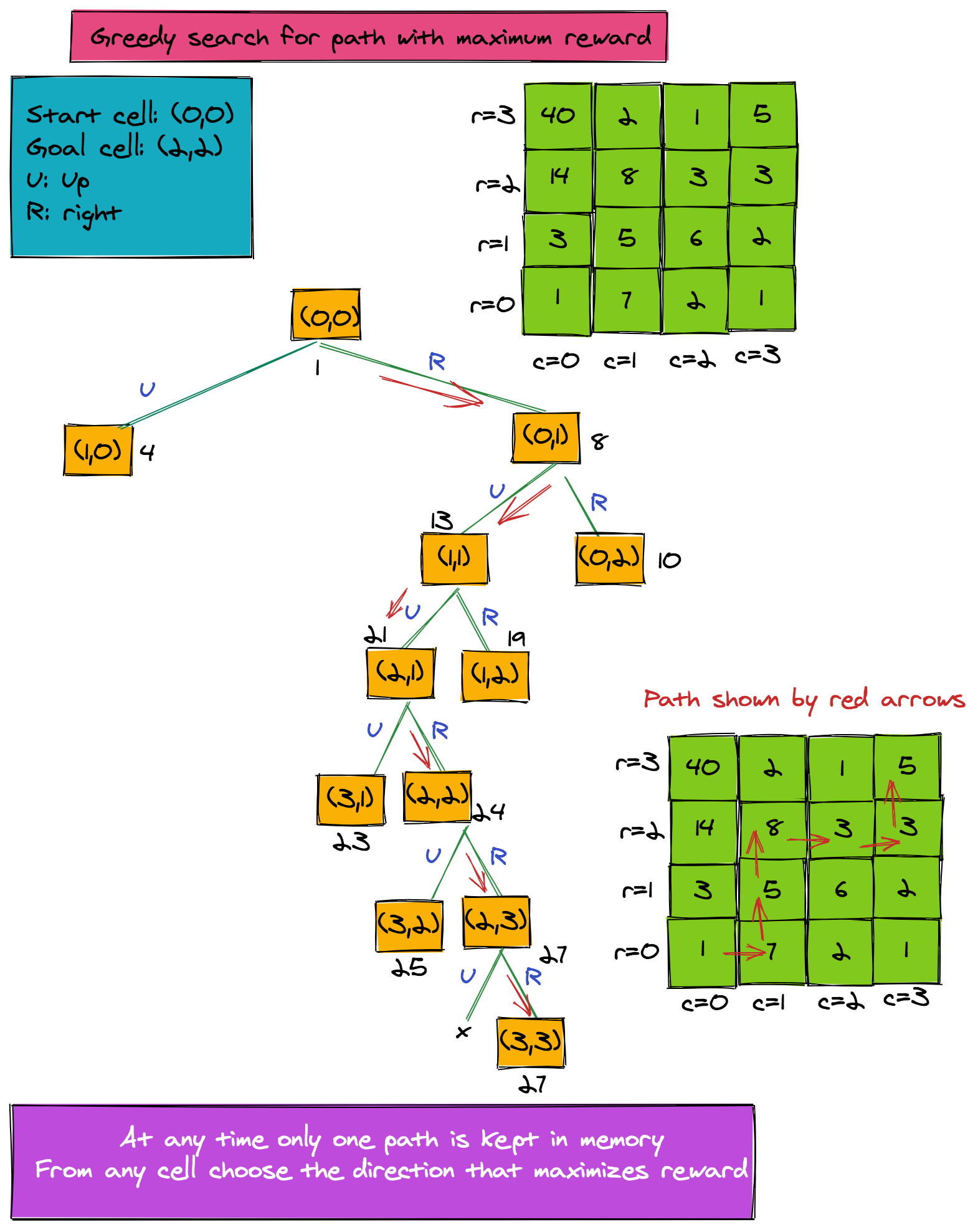
The figure below illustrates how a greedy algorithm solves the problem. The hope is that by taking the locally best solutions, we ultimately approximate the global best solution.

Note that for this problem, a greedy search through the grid does not give us the optimal solution. We can see that the cell (3, 0) has a reward of 40, and our algorithm never passes through this cell.

Complexity of Greedy Navigation Through the Grid

For any path, there are (m-1) up moves and (n-1) right moves, hence the total path can be found in (m+n-2) moves. Therefore the complexity of the greedy algorithm is O(m+n), with a space complexity of O(1). It is very tempting to use this algorithm because of its space and time complexity-- however, there are no guarantees that it would give the most optimal accumulated reward.

1routine greedyNavigate
2Input: Matrix w of dimensions m * n containing reward for each cell,
3Start cell coordinates: (0, 0)
4Goal cell coordinates: (m-1, n-1)
5Output: Path found and the accumulated reward on that path
6
7// (r, c) denotes (row, column) coordinates
81. total = 0
92. (r, c) = (0,0)
103. while (r, c) != goal
11    a. total = total + w[r, c]
12    b. print (r, c)           // print coordinates of the cell
13    // check if we are in top row
14    c. if (r == m-1)
15        c = c+1             // go right. no other choice
16    // check if we are in rightmost col
17    d. if (c == n-1 )
18        r = r+1             // go up, no other choice
19    // greedily select either up or right move
20    e. if w[r+1, c] > w[r, c+1]
21            r = r+1                 // move up
22        else
23            c = c+1                 // move right
244. Print goal
255. return total                     // return accumulated reward

xxxxxxxxxx

let total = 0;

let r = 0, c = 0;

while (r !== m-1 || c !== n-1)

{

    total += w[r][c];

    console.log(r + ", " + c);

    if (r === m-1)

        c++;

    else if (c === n-1 )

        r++;

    else if (w[r+1][c] > w[r][c+1])

        r++;

    else

        c++;

}

console.log(m-1 + ", " + (n-1));

return total;