Greedy Algorithm for Activity Selection

Here is the pseudo-code that solves the activity selection problem using a greedy strategy. We may assume that the intervals are sorted according to their finish times.

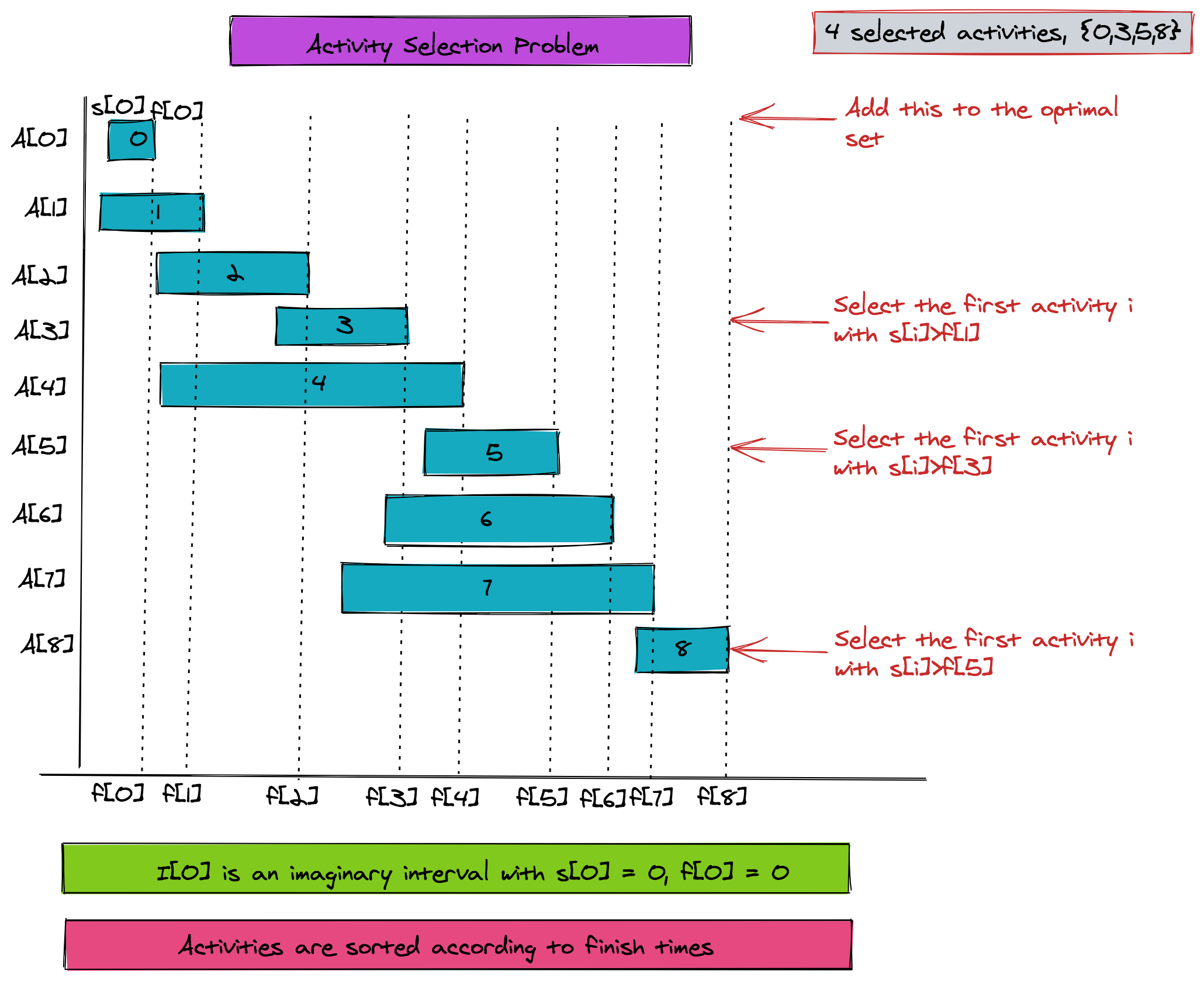
The problem parameters along with the solution are both shown in the figure below. The algorithm first adds activity 0 to the selected pool. Next, it iteratively finds the first activity whose start time is greater than the finish time of the last added activity. It then adds it to the pool.

Time Complexity of Activity Selection

If we analyze the pseudo-code, we can see that only one pass is made through all the activities and hence the time complexity is O(n). There is no additional intermediate space involved for storing an array or matrix, making it O(1) space complexity.

However, we made an initial assumption that the activities are sorted according to finish times. If the activities are not sorted, then we can add O(n log n) overhead for sorting, making the time complexity O(n log n) and space complexity O(1).

1Routine selectActivity
2Input: Finish time array f
3Output: Selected activity array S and total activities in S
4
51. count = 0
62. S[count] = 0
73. lastInd = 0                  // index of last activity added to S
84. for i = 1..(n-1)
9    a. if s[i] >= f[lastInd]    // add i to selected activity set S
10        then
11        {
12            i. count = count + 1
13            ii. S[count] = i
14            iii. lastInd = i
15        }
165. return (count + 1) and S

xxxxxxxxxx

function selectActivity(f) {

    let count = 0;

    let S = [];

    S[count] = 0;

    let lastInd = 0; // index of last activity added to S

    for (let i = 1; i < f.length; i++) {

        if (f[i] >= f[lastInd]) {

            count = count + 1;

            S[count] = i;

            lastInd = i;

        }

    }

    return [S, count + 1];

}