AlgoDaily - Implementing Graphs: Edge List, Adjacency List, Adjacency Matrix

Home > Data Structures and Algorithms 🚀 > Draw a Graph > Implementing Graphs: Edge List, Adjacency List, Adjacency Matrix

For many students, the graph data structure can be intimidating and difficult to learn. In fact, some of their properties can be baffling to even experienced developers and computer science graduates who haven't worked with them for a while.

But graphs are interesting and integral, as they are a vital way of modeling and displaying information in the world around us. We can use graphs to do incredible things with computers. As an example, social networks are simply huge graphs at their core. Companies like LinkedIn and Google utilize many graph algorithms understand complex networks and relationships.

Before we dive into more theory, let us provide some motivation for learning graphs.

What are graphs and what can we do with them?

Much of this is review from The Simple Reference To Graphs. If you already have the basics down, feel free to skip to the implementation parts later in the guide.

In purely layman's terms, a graph is a group of dots connected by lines. You've seen them plenty of times. Programmatically, these "dots" represent things, and these lines are to demonstrate connections between things. We can use graphs to model relationships in the world.

For example:

Facebook friend networks are a graph where each person is a "dot" or a node, and the friendships and connections between people are lines.
Google Maps uses a series of nodes and lines to model the road network and give you directions to your final destination.
The Internet is a really a giant graph where web pages are dots and the links between pages are lines.

We can meaningful model groups of relationships, find relations between people, find the shortest path between two points, model objects in space, and document structures all using this concept of nodes connected by edges.

Understanding the Concepts

Some quick refreshers:

Terminology

When people talk about graphs, they don't use the terms dots and lines. Instead, each dot is called a node or vertex, and each line is called an edge.

Formal Definition

A formal definition of a graph is a "data structure that consists of a finite collection of vertices and edges that represents relationships".

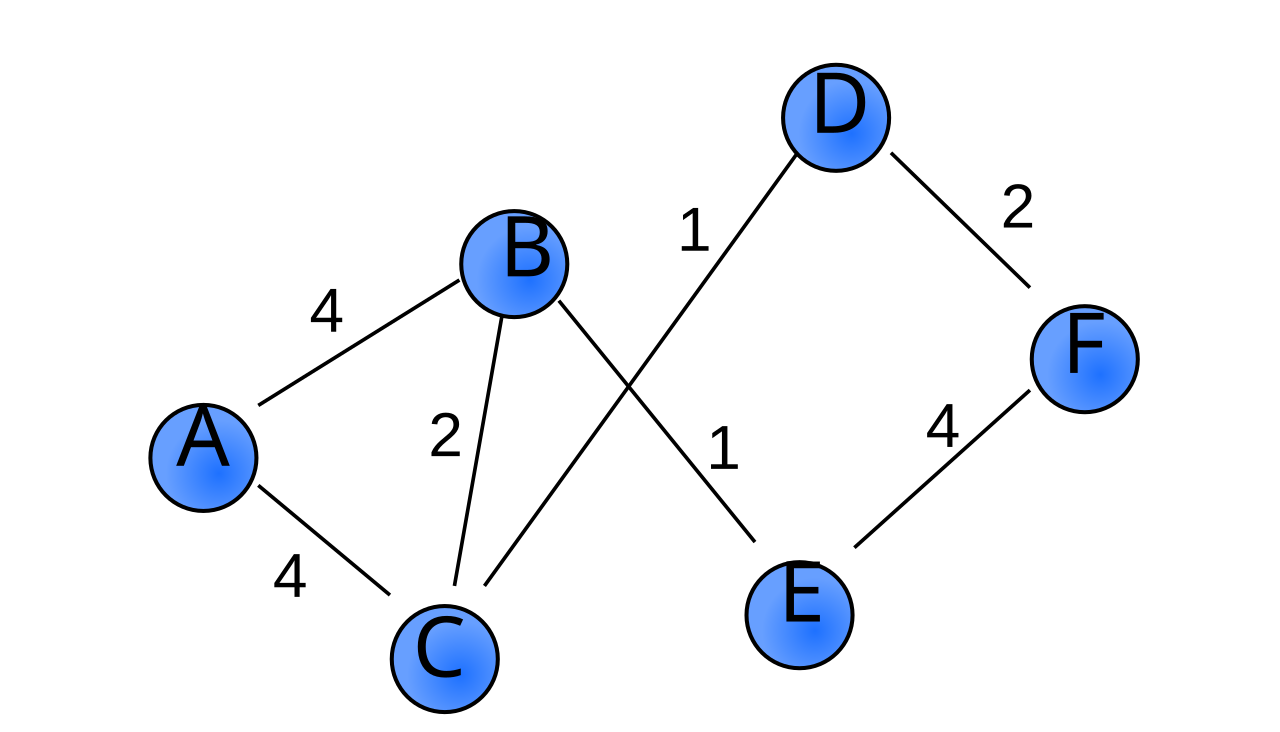
Edges

The edges of a graph are represented as ordered or unordered pairs depending on whether or not the graph is directed or undirected.

Edges of a graph might have weights indicating the strength of that link between vertices.

Are you sure you're getting this? Click the correct answer from the options.

What are the basic components of a graph?

Click the option that best answers the question.

Nodes/Vertices and Edges
Lines
Nodes and dots
Array and lists

Last concept to revisit, and we'll move on to implementation!

Undirected Graphs

Undirected graphs have edges that do not have a direction. With undirected graphs, we can represent two-way relationships so an edge can be traversed in both directions.

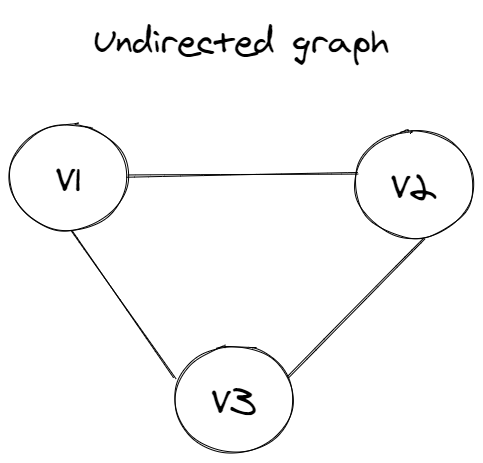
In theory, an undirected graph could be used at Facebook, since both users have to friend each other to build a friendship.

Directed Graphs

Directed graphs have edges with direction. With directed graphs, we can represent one-way relations so an edge can be traversed in a single direction.

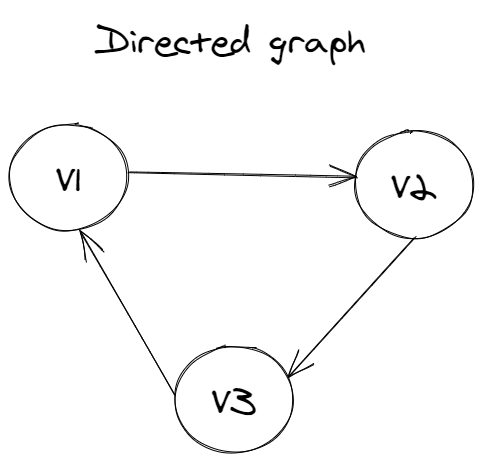
A directed graph would be used at Twitter, since the relationship can be one-sided, and you don't need to follow each of your followers.

Build your intuition. Fill in the missing part by typing it in.

What is the type of graph that represents two-way relationships? In this type, an edge can be traversed in both directions.

Write the missing line below.

Problems For Graphs

The applications of graphs are overwhelming in nature! No wonder they're so important. Here's but a few more examples.

1) Finding the shortest path.

2) Finding the best starting point.

3) Breadth-first and depth-first traversal.

4) Searching, inserting, deleting from a tree or linked list.

5) Graph classification to discriminate between graphs of different classes.

6) Finding the missing relationships between entities through link prediction.

7) Node classification.

Let's test your knowledge. Is this statement true or false?

Breadth-first and depth-first traversals are two kinds of search algorithms for trees and graphs.

Press true if you believe the statement is correct, or false otherwise.

Edge Lists

Now that we're all caught up on the fundamentals of graphs, let's talk implementation!

The first implementation strategy is called an edge list. An edge list is a list or array of all the edges in a graph. Edge lists are one of the easier representations of a graph.

In this implementation, the underlying data structure for keeping track of all the nodes and edges is a single list of pairs. Each pair represents a single edge and is comprised of the two unique IDs of the nodes involved. Each line/edge in the graph gets an entry in the edge list, and that single data structure then encodes all nodes and relationships.

In the graph above, we have three nodes: 1, 2, and 3. Each edge is given an index and represents a reference from one node to another. There isn't any particular order to the edges as they appear in the edge list, but every edge must be represented. For this example, the edge list would look like the attached snippet:

1edge_list = [
2	[1,2],
3	[2,3],
4	[3,1]
5]

Due to the fact that an edge list is really just an array, the only way to find something in this array is by iterating through it.

For example, if we wanted to see if vertex 1 was connected to vertex 2, we'd need to iterate through the previous array and look for the existence of a pair [1,2] or [2,1].

This is fine for this specific graph since it only has three vertices and three edges. But as you can imagine, having to iterate through a much larger array would increase complexity.

Checking to see if a particular edge existed in a large array isn't guaranteed to have a sense of order, and the edge could be at the very end of the list. Additionally, there may not be any edge at all, and we'd still have to iterate through the whole thing to check for it. This would take linear time, O(E) (E being the number of edges) to get it done.

Please find the implementation of an edge list attached.

xxxxxxxxxx
our_graph.print_graph()
 
class Node:
    def __init__(self, name):
        self.name = name
        self.edge_list = []
​
    def get_name(self):
        return self.name
​
    def get_edges(self):
        return self.edge_list
​
class Edge:
    def __init__(self, dest, weight=1):
        self.dest_vertex = dest
        self.weight = weight
​
    def get_weight(self):
        return self.weight
​
    def get_dest_vertex(self):
        return self.dest_vertex
​
class Graph:
    def __init__(self):
        self.nodes = set()
​
    def add_edge(self, v1, v2, weight):
        return v1.get_edges().append(Edge(v2, weight)) and v2.get_edges().append(Edge(v1, weight))
​

Adjacency Matrix

While an edge list won't end up being the most efficient choice, we can move beyond a list and implement a matrix. For many, a matrix is a significantly better kinesthetic representation for a graph.

An adjacency matrix is a matrix that represents exactly which vertices/nodes in a graph have edges between them. It serves as a lookup table, where a value of 1 represents an edge that exists and a 0 represents an edge that does not exist. The indices of the matrix model the nodes.

Once we've determined the two nodes that we want to find an edge between, we look at the value at the intersection of those two nodes to determine whether there's a link.

In this illustration, we can see that the adjacency matrix has a chain of cells with value 0 diagonally. In fact, this is true of most graphs that we'll deal with, as most won't be self-referential. In other words, since node 2 does not (or can not) have a link to itself, if we were to draw a line from column 2 to row 2, the value will be 0.

However, if we wanted to see if node 3 was connected to node 1, we'd find there to be a relationship. We could find column 3, row 1, and see that the value is 1, which means that there is an edge between these two nodes.

Adjacency matrices are easy to follow and represent. Looking up, inserting and removing an edge can all be done in O(1) or constant time. However, they do have a downfall, which is that they can take up more space than is necessary. An adjacency matrix always consumes O(V^2) (V being vertices) amount of space.

Nevertheless, adjacency matrices are definitely a step up from an edge list. Their representation would look like this:

xxxxxxxxxx
 
matrix = [
  [0, 1, 1],
  [1, 0, 1],
  [1, 1, 0]
]

Are you sure you're getting this? Fill in the missing part by typing it in.

The function below returns an object for the specified vertex. Fill in the missing snippet for the method.

TEXT/X-JAVA

1public Vertex getVertex(int index) {
2    return vertices.get(___________);
3}

Write the missing line below.

Here's a complete implementation of an adjacency matrix.

xxxxxxxxxx
print(g)
 
# Original code in Java
class Graph:
    def __init__(self, num_vertices):
        self.num_vertices = num_vertices
        self.adj_matrix = [[False] * num_vertices for _ in range(num_vertices)]
​
    def add_edge(self, i, j):
        self.adj_matrix[i][j] = True
        self.adj_matrix[j][i] = True
​
    def remove_edge(self, i, j):
        self.adj_matrix[i][j] = False
        self.adj_matrix[j][i] = False
​
    def __str__(self):
        s = ""
        for i in range(self.num_vertices):
            s += str(i) + ": "
            s += " ".join(["1" if j else "0" for j in self.adj_matrix[i]]) + "\n"
        return s
​
​
g = Graph(4)
g.add_edge(0, 1)
g.add_edge(0, 2)
g.add_edge(1, 2)
g.add_edge(2, 0)
g.add_edge(2, 3)
​

Try this exercise. Click the correct answer from the options.

What does the toString() method do in the previous code?

Click the option that best answers the question.

Finds the average of all the vertices in the matrix
Counts the total of all vertices in the matrix
Returns a String containing all the attributes of the matrix
Stores the name of the matrix in a String

Adjacency Lists

Let's say both edge lists and adjacency matrices seem to fail our requirements, what do we do? Well, we combine them together and create a hybrid implementation!

This is what an adjacency list is-- a hybrid between an adjacency matrix and an edge list. An adjacency list is an array of linked lists that serves the purpose of representing a graph. What makes it unique is that its shape also makes it easy to see which vertices are adjacent to any other vertices. Each vertex in a graph can easily reference its neighbors through a linked list.

Due to this, an adjacency list is the most common representation of a graph. Another reason is that graph traversal problems often require us to be able to easily figure out which nodes are the neighbors of another node. In most graph traversal interview problems, we don't really need to build the entire graph. Rather, it's important to know where we can travel (or in other words, who the neighbors of a node are).

In this illustration, each vertex is given an index in its list. The list has all of its neighboring vertices stored as a linked list (can also be an array) adjacent to it.

For example, the last element in the list is the vertex 3, which has a pointer to a linked list of its neighbors. The list that is adjacent to vertex 3 contains references to two other vertices (1 and 2), which are the two nodes that are connected to the node 3.

Thus, just by looking up the node 3, we can quickly determine who its neighbors are and, by proxy, realize that it has two edges connected to it.

This all results from the structure of an adjacency list making it easy to determine all the neighbors of one particular vertex. In fact, retrieving one node's neighbors takes constant or O(1) time, since all we need to do is find the index of the node we're looking for and pull out its list of adjacent vertices.

Please see the implementation of adjacency list attached.

xxxxxxxxxx
 
# Class representing a simple graph using an edge list converted to adjacency list
class Graph:
    # Basic constructor method
    def __init__(self, edge_list, num_of_nodes):
        # Convert edge list to adjacency list,
        # represented with a multi-dimensional array
        self.adjacency_list = [[] for _ in range(num_of_nodes)]
 
        # Add edges to corresponding nodes of the graph
        for (origin, dest) in edge_list:
            self.adjacency_list[origin].append(dest)
 
 
# Helper method to print adjacency list representation
def print_graph(graph):
    for origin in range(len(graph.adjacency_list)):
        # print current vertex and all its neighboring vertices
        for dest in graph.adjacency_list[origin]:
            print(f'{origin} —> {dest} ', end='')
        print()
 
 
if __name__ == '__main__':
    # Set up an edge list and number of nodes
    edge_list = [(0, 1), (1, 2), (2, 3), (0, 2), (3, 2), (4, 5), (5, 4)]
    num_of_nodes = 6
 
    graph = Graph(edge_list, num_of_nodes) 
    print_graph(graph)

Conclusion

Chances are if you build anything complex with computation, you'll use a graph whether you know it or not. Understanding the basics of implementing graphs and is fundamental to unpacking some of the most complicated and well-known computer science problems.

One Pager Cheat Sheet

The graph data structure, though often intimidating to students, is a crucial tool for modeling information, allowing for complex abilities like social networking, and is used by companies like LinkedIn and Google to understand networks and relationships through various graph algorithms.
A graph is a programmatic representation of connected things or entities, which uses nodes (dots) to represent items and connections (lines) between them known as edges, allowing us to model and document structures or relationships, such as those in social networks or internet web pages.
In graph terminology, dots are referred to as nodes or vertices, lines are called edges, and the graph itself is a data structure representing relationships; edges can be ordered or unordered depending on if the graph is directed or undirected, and may have weights signifying the link strength between vertices.
A graph in computer science and mathematics consists of two essential components, nodes/vertices representing distinct entities, and edges depicting the relationships or interactions between these entities, with attributes like direction and weight indicating specific aspects of these relationships.
The concept of a social network can be modeled as a graph, where users are represented as vertices and friendship relations are represented as edges, as demonstrated with a graph containing Peter, Kevin, Jake, and Daniel.
Undirected graphs represent two-way relationships with edges that can be traversed in both directions, while directed graphs represent one-way relations with edges that can be traversed in a single direction.
In graph theory, there are two types of graphs: undirected graphs, which represent two-way relationships and can be traversed in both directions, and directed graphs, which represent one-way relationships and can only be traversed in one direction.
The applications of graphs include finding the shortest path, finding the best starting point, breadth-first and depth-first traversal, searching, inserting, deleting from a tree or linked list, graph classification, finding missing relationships through link prediction, and node classification.
The statement affirms that breadth-first and depth-first traversals are search algorithms used for navigating 'tree' and 'graph' data structures in a horizontal and vertical manner respectively.
An edge list is an implementation strategy for graphs where all the edges are stored in a single list of pairs, each pair representing an edge through the two unique IDs of the nodes involved.
To find something in an edge list, an array-like data structure, one needs to iterate through it which is a linear time operation (O(E)), leading to increased complexity in the case of larger arrays.
An adjacency matrix is a type of matrix used to represent the vertices/nodes and connection/links in a graph, where 1 indicates an existing edge and 0 indicates a non-existing one, enabling lookup, insertion, and removal of an edge in O(1) or constant time, but consumes O(V^2) space, where V is the number of vertices.
The get() method, used in the context of the adjacency matrix graph representation, takes an index as a parameter to return the vertex at that particular index in the vertices list, representing each vertex or node in the graph as a list.
This provides a complete implementation of an adjacency matrix.
The toString() method in Java, overridden in the Matrix class definition, creates a readable string representation of an object by returning a String that contains all attributes of the object, such as the size and values of a matrix, thereby providing an efficient way to view all data related to the object.
An adjacency list is a hybrid of an edge list and an adjacency matrix, serving as the most common representation of a graph due to its linked list structure that makes it easy to identify neighboring vertices, which is crucial for graph traversal problems.
The illustration depicts an adjacency list where each vertex has an index in its list with neighboring vertices stored as a linked list or array, enabling quick determination of a node's neighbors and their connections, taking a constant or O(1) time to retrieve.
Understanding the basics of implementing graphs is fundamental to solving complex computer science problems, since graphs are likely utilized in any complex computation.

What are graphs and what can we do with them?

Understanding the Concepts

Terminology

Formal Definition

Edges

Are you sure you're getting this? Click the correct answer from the options.

Click the option that best answers the question.

Undirected Graphs

Directed Graphs

Build your intuition. Fill in the missing part by typing it in.

Problems For Graphs

Let's test your knowledge. Is this statement true or false?

Edge Lists

Adjacency Matrix

Are you sure you're getting this? Fill in the missing part by typing it in.

Try this exercise. Click the correct answer from the options.

Click the option that best answers the question.

Adjacency Lists

Conclusion

One Pager Cheat Sheet

Programming Categories

Popular Lessons