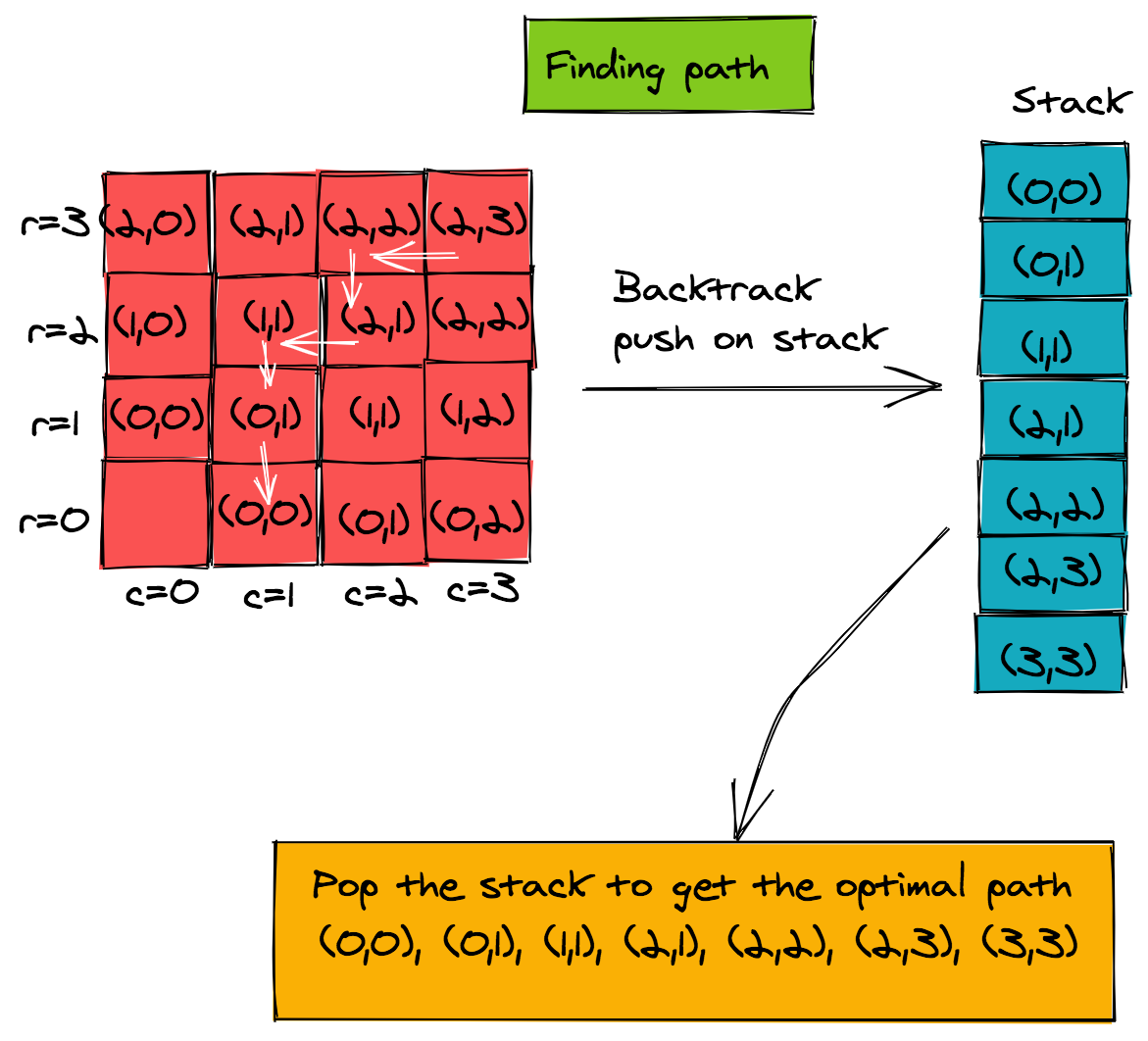
Once we have the direction matrix, we can backtrack to find the best path, starting from the goal cell (m-1, n-1). Each cell's predecessor is stored in the matrix d.

If we follow this chain of predecessors, we can continue until we reach the start cell (0, 0). Of course, this means we'll get the path elements in the reverse direction. To solve for this, we can push each item of the path on a stack and pop them to get the final path. The steps taken by the pseudo-code are shown in the figure below.

1Routine: printPath
2Input: direction matrix d
3Intermediate storage: stack
4
5// build the stack
61. r = m-1
72. c = n-1
83. push (r, c) on stack
94. while (r!=0 && c!=0)
10    a. (r, c) = d[r, c]
11    b. push (r, c) on stack
12// print final path by popping stack
135. while (stack is not empty)
14    a. (r, c) = stack_top
15    b. print (r, c)
16    c. pop_stack

xxxxxxxxxx

let stack = [];

​

let r = m - 1;

let c = n - 1;

stack.push([r, c]);

​

while (r !== 0 && c !== 0) {

    let pair = d[r][c];

    r = pair[0];

    c = pair[1];

    stack.push([r, c]);

}

​

while (stack.length !== 0) {

    let pair = stack[stack.length - 1];

    console.log("(" + pair[0] + ", " + pair[1] + ")");

    stack.pop();

}