From Naive to Smart: Maximizing Grid Rewards

Ah, the grid! Picture it as a treasure map where each cell has its own hidden gem (or, let's say, reward). Our trusty robot wants to navigate this map to find the ultimate treasure—the maximum reward. But there's a catch! The robot can only move up or to the right. How do we make sure our robotic friend picks the richest path?

The Brute-Force Way: Recursive Enumeration

If you've read the tutorial on recursion and backtracking, you know that you can enumerate all paths using backtracking. It's like the robot taking a stroll, noting down each path and the rewards it accumulates.

Steps for Recursive Enumeration

1. Walk through all possible paths while keeping track of the reward for each path.
2. Select the path that garners the maximum reward.

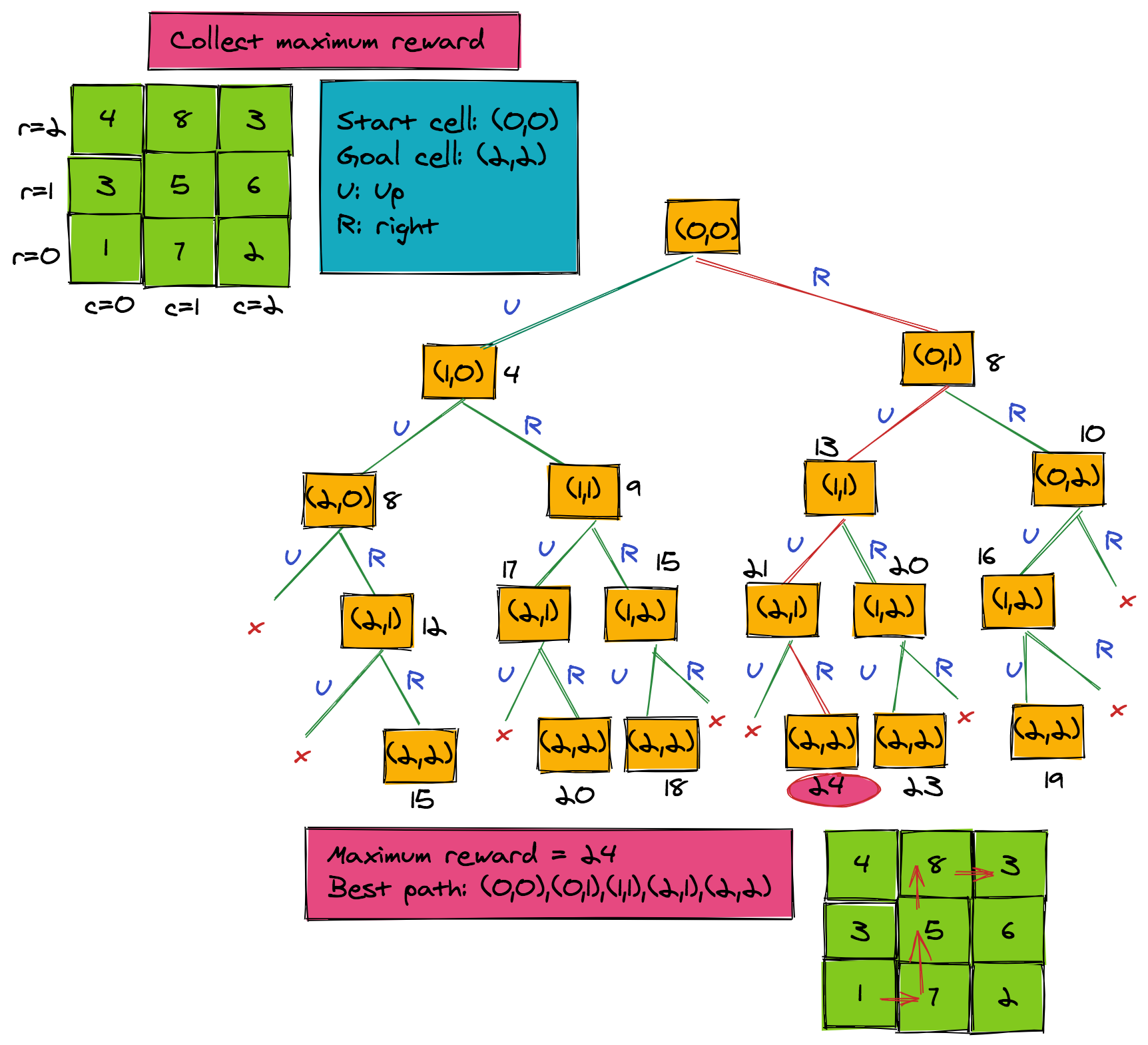
The Downside: Exponential Complexity

This might sound like a simple plan, but it's a costly one. Just like our previous Fibonacci example, this naive approach has an exponential time complexity of $O\left(2^{mn}\right)$. That's a lot of calculations, and our robot doesn't have all day!

Enter Dynamic Programming: A Smarter Approach

Let's switch gears and bring dynamic programming into the picture. Just like we did with the Fibonacci numbers, we can avoid recalculating rewards for the same cell multiple times. This is how dynamic programming turns our robot into a strategic treasure hunter.

Steps to Implement Dynamic Programming

1. Create a 2D array, dp, with dimensions (m \times n).
2. Initialize dp[0][0] with the reward of the starting cell.
3. Loop through the grid, and for each cell (i, j), update dp[i][j] as the maximum reward you can get by either coming from the top cell dp[i-1][j] or the left cell dp[i][j-1], plus the reward at (i, j).
4. The value at dp[m-1][n-1] will be the maximum reward.

By following these steps, we reduce our time complexity from exponential to linear, $O(m\times n)$, which is a significant improvement.