Heap Sort

Finally, heap sort is based on comparisons. We can say that it is an improved version of selection sort. It actually visualizes the array elements as heap.

Heap

A heap is a tree-based structure. The definition of one is that it is a complete binary tree and all the nodes are greater than their children. A heap is said to be a Min-Heap if all the nodes are smaller than their children, otherwise it will be considered as a Max-Heap.

How to heapify a tree?

A function called heapify can be used on all non-leaf nodes of the heap in order to make a Max-Heap.

Implementation of HeapSort

Consider an Array which is to be sorted using heap sort. To begin, we will create Max-Heap using the elements of Array.

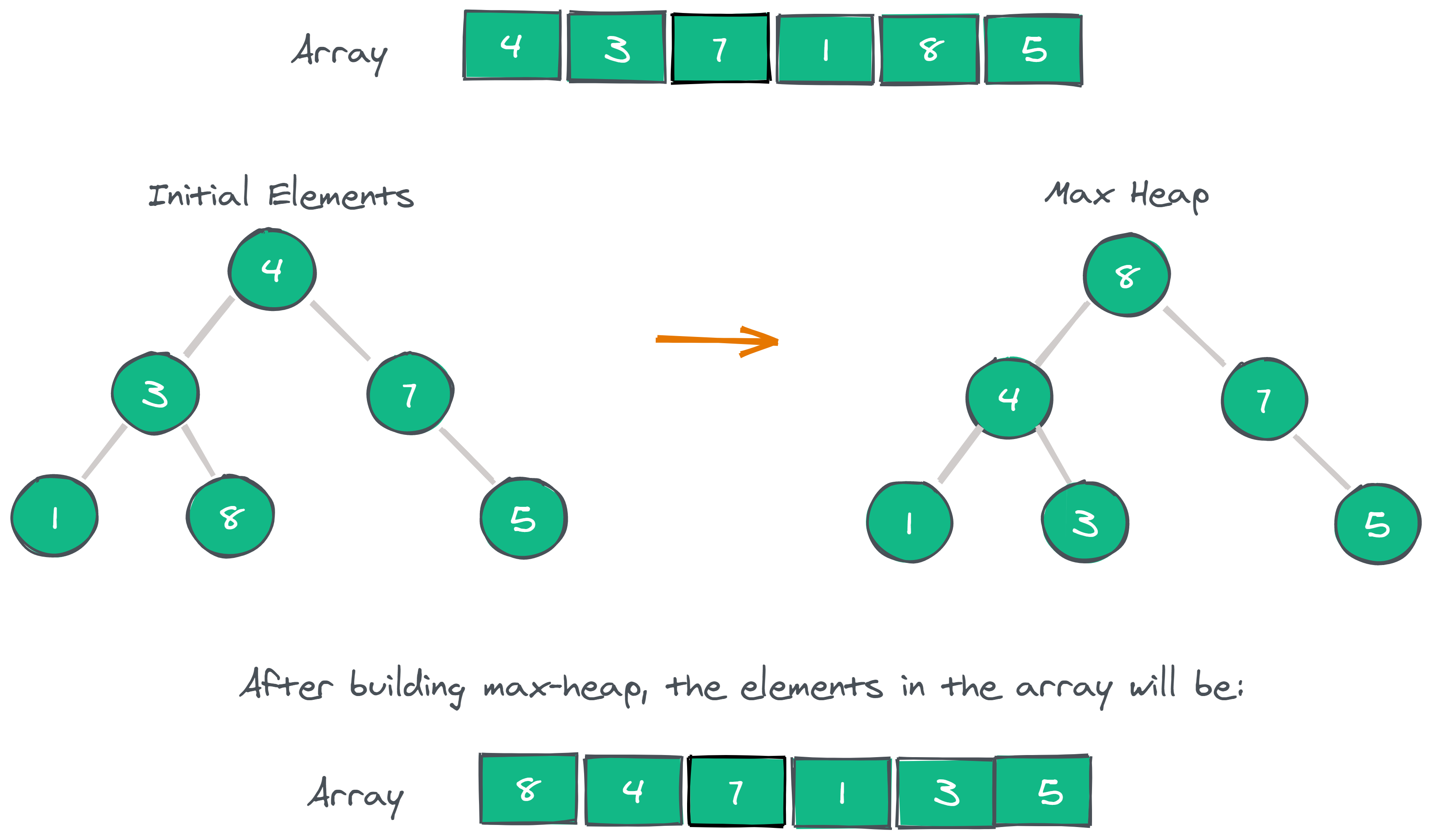
The first element of the array would be the largest, so we will swap this element with the last one. We will heapify the Max-Heap but exclude the last element as it is already in its correct position. After that, we will decrease the length of the array by one. Then, we will repeat this step until all the elements in the array are in their correct position.

The following steps should be taken in order to sort the above Array.

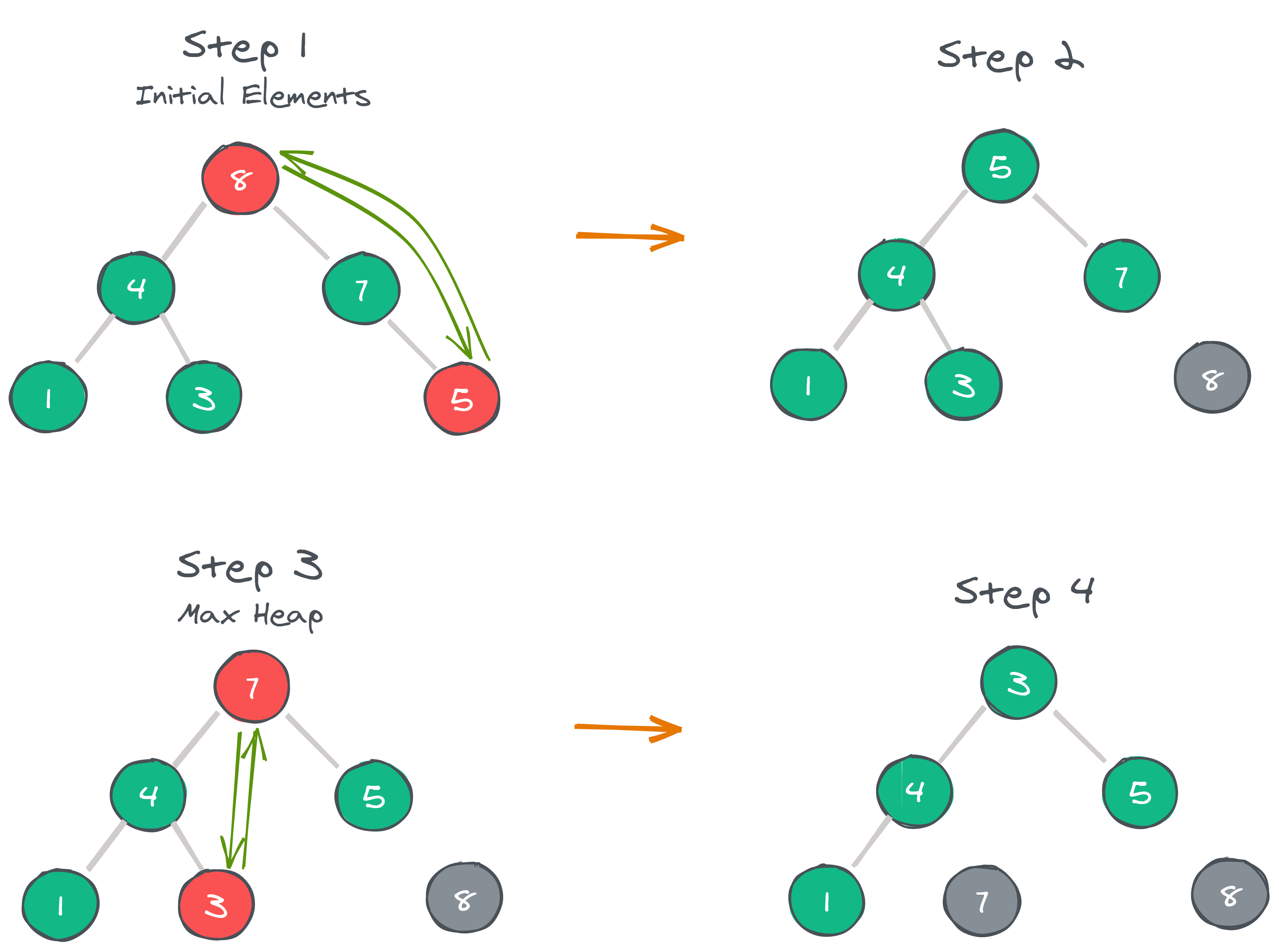
Step 1: 8 is swapped with 5.
Step 2: 8 is disconnected from the heap as 8 is in the correct position now and.
Step 3: Max-heap is created and 7 is swapped with 3.
Step 4: 7 is disconnected from the heap.
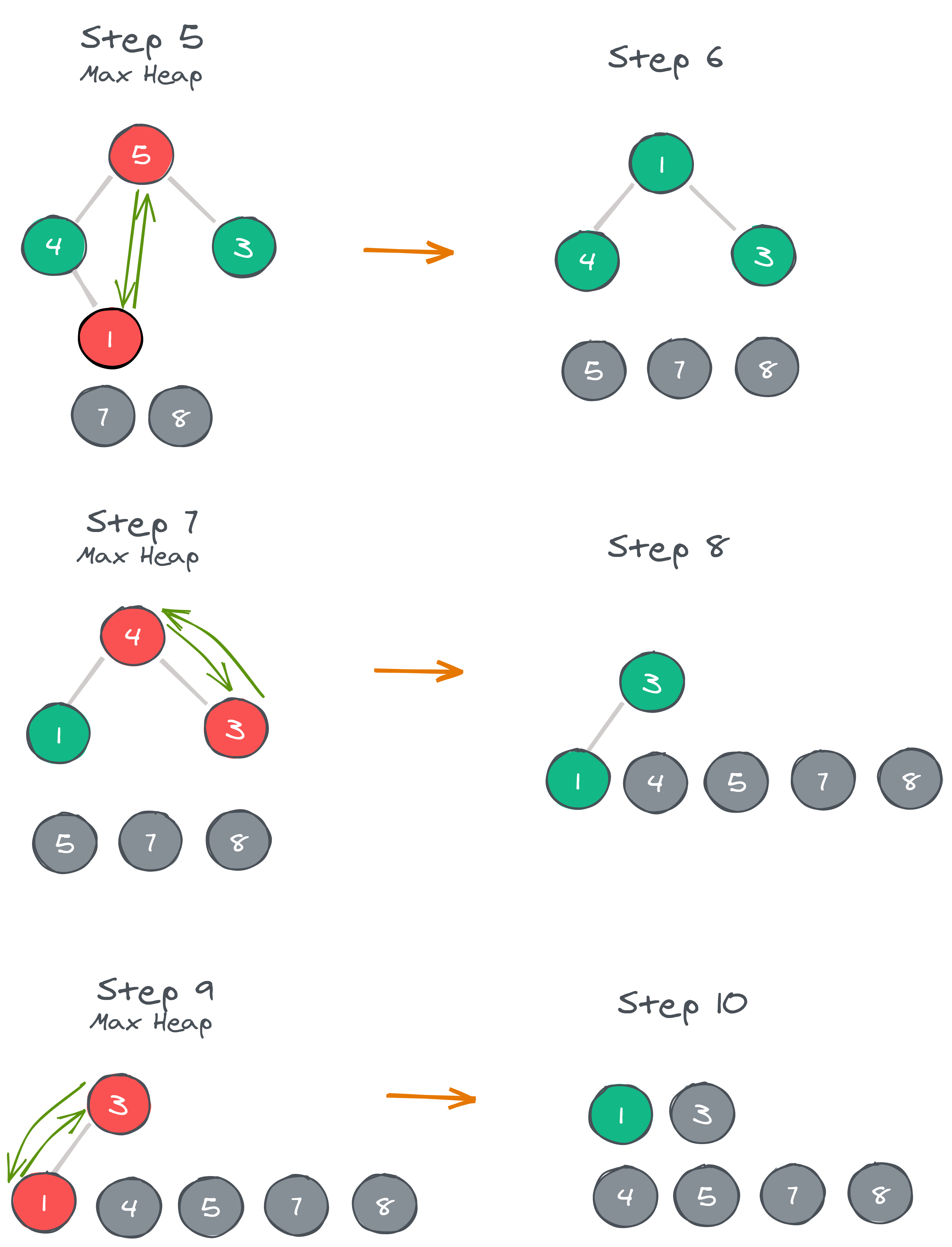
Step 5: Max heap is created and 5 is swapped with 1.
Step 6: 5 is disconnected from the heap.
Step 7: Max heap is created and 4 is swapped with 3.
Step 8: 4 is disconnected from the heap.
Step 9: Max heap is created and 3 is swapped with 1.
Step 10: 3 is disconnected

The following illustrations will demonstrate the above steps.

After all the steps, we will get the sorted array.