Today’s Goal: Make Union–Find your new party trick
By the end, you’ll be able to:
- Explain what Union–Find is (without hand-waving).
- Spot when to use it in interviews.
- Crush “are these two things connected?” problems.
Why this matters (aka: where algorithms meet real life)
Think friend groups at a party. People drift, groups merge, someone asks, “Hey, are Alex and Sam in the same circle?” That’s a connectivity question—and computers get those constantly. We want a fast way to track groups as they form and check if two people belong together.
Enter Union–Find (also called Disjoint Set Union, or DSU): your efficient answer to “together or not?”
Understanding the Core of Union-Find: Key Concepts and Operations
The Union-Find algorithm, also known as the disjoint-set data structure, is like a social organizer for a set of elements. Imagine these elements as people at a party, and the algorithm helps figure out who belongs to which friend circle. The elements are partitioned into disjoint (non-overlapping) subsets, like different circles of friends who don't mix.
The Building Blocks: Sets and Objects
In the context of graphs, these sets are usually represented by vertices or nodes. However, these could be any objects you are working with. Think of them as the individual attendees at our hypothetical party.
The Two Pillars: Find and Union Operations
The Union-Find algorithm performs its magic through two primary operations: Find and Union.
Find Operation:
- What it Does: Determines the subset that an element belongs to.
- Real-world Analogy: Imagine asking, "Which friend circle does Alice belong to?"
- Significance: Helps you ascertain if two elements are in the same subset, answering the question, "Is there a path connecting Alice to Bob?"
Union Operation:
- What it Does: Merges two disjoint subsets into one.
- Real-world Analogy: Imagine merging two separate friend circles into one larger group.
- Significance: Creates a connection between two objects, effectively creating a path between them.
By mastering these two operations, you'll be well-equipped to tackle problems involving network connectivity, disjoint sets, or partitioning a set into non-overlapping subsets.
Union–Find in one picture

Imagine a bunch of islands (disconnected groups).
- Union = build a bridge between two islands (now they’re one bigger island).
- Find = ask, “Which island is this person on?” If two people have the same island leader, they’re connected.
Under the hood, Union–Find keeps little trees of members with a “representative” at the top. With tricks like path compression and union by rank/size, lookups are basically instant.
Where you’ll use it (especially in interviews)
If the problem smells like connectivity or merging groups, think Union–Find:
- Connected components: “How many groups are there?”
- Cycle detection (undirected graphs): “Does adding this edge create a loop?”
- Grid/maze problems: “Do start and finish end up connected?”
- Network questions: “When does the whole network become connected?”
- Kruskal’s MST: Sorting edges + Union–Find = chef’s kiss.
Quick mental checklist
- Are we merging things over time? → Union
- Are we asking “same group?” a lot? → Find
- Do we care about speed with tons of merges/lookups? → Use DSU with path compression + union by size
Ready to wire up those islands? Let’s make Union–Find do the heavy lifting.
Union-Find, Explained Simply
Union-Find (also called Disjoint Set Union, DSU) is a tiny toolkit for tracking which items belong together. Think of it as a label maker for groups: it can quickly tell you whether two people are in the same “friend circle,” and it can glue two circles together.
What We’re Managing: Disjoint Sets
Imagine n people split into separate circles. Two rules:
- No overlap. Each person is in exactly one circle. If Sarah is in
S1, she isn’t inS2. Two questions we care about.
- Find: “Which circle is Sarah in?”
- Union: “Can we merge
S1andS2into one circle?”
Example circles:
S1 = {Alice, Bob, Carol}S2 = {Dave, Eve}S3 = {Grace, Helen, Frank}
They don’t overlap, so they’re perfect for Union-Find.
The Two Moves
Find(x) Returns the representative (the label) of x’s circle. Example:
Find(Bob) → S1.Union(a, b) Merges the circles that contain
aandb. Example:Union(S1, S2)→{Alice, Bob, Carol, Dave, Eve}becomes one circle.
That’s the whole API.
How It Works Under the Hood
Internally, each circle is a tiny tree:
- Every person points to a “parent.”
- The root of the tree is the circle’s representative.
So:
- Find(x) walks parent pointers until it reaches the root (the label of x’s circle).
- Union(a, b) connects one root under the other, turning two trees into one.
Speed Tricks (Why It’s So Fast)
Path Compression (during Find) After we climb to the root, we flatten the path: everyone we touched points directly to the root. Future Finds get almost instant.
Union by Rank/Size Always attach the smaller tree under the larger tree’s root. This keeps trees shallow, which keeps Finds quick.
With both tricks, operations are effectively near O(1) on average—even for huge datasets.
Quick Mental Model
- Label maker:
Findreads the label;Unioncombines labels. - Family tree: the root is the “head of the family.”
Findwalks up to the head;Unionmarries two families by making one head point to the other. - Autotune: path compression and union-by-size keep the trees short so everything stays fast.
Demystifying Cycles in Graphs: A Union-Find Exploration
Our mission is to find out if a network of roads in a city forms a loop or not. In technical terms, we want to see if an undirected graph contains a cycle. If you process all the roads and don't find any loops, congratulations! You've found an acyclic graph.
The Case at Hand: Does This Graph Have a Cycle?
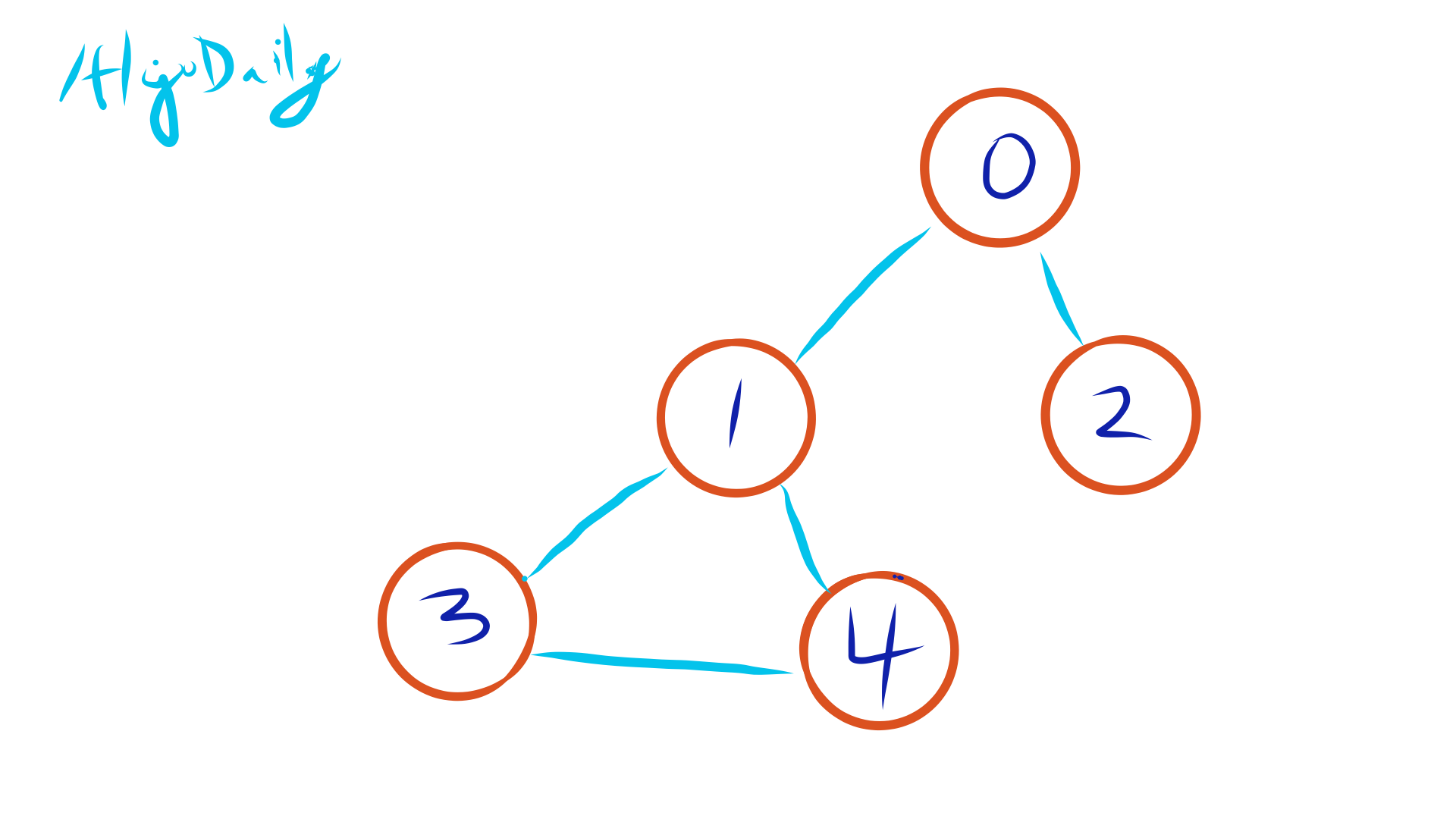
Setting Up the Investigation Board: Initial Steps
First, let's consider each intersection (or vertex) as its own isolated neighborhood. To help us keep track of these neighborhoods, we'll use a 'parent array.'
Visual Snapshot of the Investigation Board
In this image, the number inside each circle represents a vertex, and the number below it signifies its 'parent.' Initially, each vertex is its own parent, representing isolated neighborhoods.
The Investigation Begins: Processing Edges
The First Clue: Edge (0,1)
Let's start with the road connecting intersections 0 and 1 and see if they're part of the same neighborhood.
What Did We Find?
Find(0)returns0: Intersection0is its own neighborhood.Find(1)returns1: The same goes for intersection1.
Since both intersections belong to different neighborhoods, there is no loop or cycle for this road.
We would continue this process for each road in our network. If we ever find a road where both intersections belong to the same neighborhood, that's our "Aha!" moment—a cycle is detected.
xxxxxxxxxx// Initialize a parent array to represent isolated neighborhoods.int[] parent = {0, 1, 2, 3, 4};// Function to identify the 'root' or 'parent' of each neighborhood.public int find(int vertex) { if (parent[vertex] == vertex) { return vertex; } return find(parent[vertex]);}// Let's check the neighborhoods of intersections 0 and 1.int rootOfVertex0 = find(0);int rootOfVertex1 = find(1);System.out.println("Find(0) = " + rootOfVertex0); // Outputs: Find(0) = 0System.out.println("Find(1) = " + rootOfVertex1); // Outputs: Find(1) = 1Union-Find in Action: Detecting Cycles in a Graph
Picture the Union-Find algorithm as a detective looking for hidden cycles within a network of interconnected nodes. Let's walk through a real-world example to see how this algorithm can unveil cycles in a graph.
The Game Plan: Three Simple Steps
Imagine a graph as a city where each intersection is a node and each road between them is an edge. The algorithm works through three basic steps:
Initialize - The Starting Point:
- What it Does: Each intersection or vertex starts off as its own isolated "neighborhood."
- Example: Think of each vertex as its own little cul-de-sac at the beginning.
Union - Building Roads:
- What it Does: Whenever you examine a road or edge (u, v), you join the neighborhoods of u and v into a larger one.
- Example: If there's a road from Main St. (u) to Elm St. (v), you'd combine these two streets into one neighborhood.
Detect Cycle - The Moment of Truth:
- What it Does: While examining a road, if you discover that both intersections are already part of the same neighborhood, you've found a cycle!
- Example: If you're looking at a road between Park Ave. (u) and Elm St. (v), and realize they're already in the same neighborhood, then you've detected a cycle.
Walking Through the Pseudocode
Let's break down the pseudocode, imagining that:
- E is the set of all roads or edges.
- u and v are individual intersections or vertices.
- X and Y are neighborhoods or subsets that u and v belong to, respectively.
1for each unvisited road (u,v) in E {
2 If the neighborhood of u is the same as that of v {
3 # They're already in the same neighborhood!
4 Print ("Cycle detected!")
5 }
6 else {
7 # Merge the two neighborhoods into one
8 Union(X, Y)
9 }
10}By following these steps, you can efficiently discover if any cycles exist within your graph—akin to finding a loop in our hypothetical city that takes you back to your starting point.
xxxxxxxxxx}public class UnionFind { int[] parent; int[] rank; public UnionFind(int size) { parent = new int[size]; rank = new int[size]; for (int i = 0; i < size; i++) { parent[i] = i; rank[i] = 0; } } public int find(int i) { if (parent[i] != i) parent[i] = find(parent[i]); return parent[i]; } public void union(int x, int y) { int rootX = find(x); int rootY = find(y); if (rootX != rootY) { if (rank[rootX] < rank[rootY]) parent[rootX] = rootY; else if (rank[rootX] > rank[rootY]) parent[rootY] = rootX; else { parent[rootY] = rootX;The Plot Thickens: Unveiling the Mystery of Union Operation
Let's continue our detective adventure to find out if our city's road network forms a loop. After investigating the first road connecting intersections 0 and 1, we've found they belong to different neighborhoods. Time to merge them!
Step 1: Merging Neighborhoods with Union(0, 1)
We will combine the neighborhoods of 0 and 1 into one. To do this, we'll update our parent array, which is our tracking mechanism.
Visual Update of the Investigation Board
Step 2: Understanding the Change in Parent Array
In the parent array, changing the value at index 0 to 1 is akin to saying that neighborhood 1 has now absorbed neighborhood 0. In family terms, it's like saying 0 is now under the 'parental guidance' of 1.
What Does This Update Mean?
This change signifies that intersection 1 is now the representative of the new, larger neighborhood {0, 1}. This merged neighborhood is like a bigger family now, and 1 is the head of the family.
Step 3: Examining the Next Clue - Edge (0,2)
Now, let's investigate another road—this one connecting intersections 0 and 2.
What will happen? Is 2 also part of this new, larger neighborhood, or is it a separate entity? Is there a loop forming, or are we still in the clear?
1Find(0) = 1
2Find(2) = 2Here's some code to illustrate how this would work:
1// Define the Union function to merge neighborhoods
2public void union(int vertex1, int vertex2) {
3 int root1 = find(vertex1);
4 int root2 = find(vertex2);
5 parent[root1] = root2;
6}
7
8// Let's merge the neighborhoods of 0 and 1
9union(0, 1);
10
11// Now, investigate another road connecting intersections 0 and 2
12int rootOfVertex0 = find(0); // Find(0) should now return 1, as 0 and 1 are in the same neighborhood
13int rootOfVertex2 = find(2); // Find(2) should return 2
14
15System.out.println("Find(0) = " + rootOfVertex0); // Outputs: Find(0) = 1
16System.out.println("Find(2) = " + rootOfVertex2); // Outputs: Find(2) = 2The Investigation Continues: Merging More Neighborhoods
As we dig deeper, we find another road connecting intersections 0 and 2. Just like before, these two intersections belong to different neighborhoods. So let's merge them!
Step 1: The Next Merge with Union(1, 2)
We bring together the neighborhoods of 1 and 2. Remember, neighborhood 1 already includes 0, so this merge will form a larger group.
Updating the Investigation Board
Step 2: Decoding the Parent Array's Latest Update
Now the value under 1 is changed to 2. This means 2 is now the head of this larger neighborhood, representing the union set {0, 1, 2}. It's like 2 has become the new head of the family, absorbing members from other smaller families.
Step 3: On to the Next Clue - Edge (1, 3)
We're not done yet! Let's turn our attention to the road connecting intersections 1 and 3. What will happen this time? Will 3 join this ever-expanding neighborhood, or is it part of a different group? Are we nearing the discovery of a loop in our city's road network?
1Find(1) = 2 # 1 is part of the bigger neighborhood represented by 2
2Find(3) = 3 # 3 is still its own neighborhoodNotice that Find(1) gives us 2 because 2 is now the parent-- and Find(3) gives us 3.
Let's look at the road that connects intersections 2 and 3. Since they're in separate neighborhoods, it's time for another merge!
Step 1: Yet Another Merge with Union(2, 3)
We're now bringing the neighborhoods of 2 and 3 together. Keep in mind that 2 already represents the large neighborhood {0, 1, 2}.
New Update on the Investigation Board
Step 2: What Does the Parent Array Say Now?
By replacing the value under 2 with 3, we signify that 3 is the new head of this even larger neighborhood, representing the union set {0, 1, 2, 3}. It's as if 3 is the new community leader, bringing together various smaller communities into one.
Step 3: The Next Piece of the Puzzle - Edge (1, 4)
We've come a long way, but our investigation isn't over. Our next clue is the road connecting intersections 1 and 4.
1Find(1) = 3 # Intersection 1 is part of the neighborhood led by 3.
2Find(4) = 4 # Intersection 4 is its own neighborhood for now.Will 4 become part of this sprawling neighborhood, or does it belong to another? Is the mystery of the loop about to be solved, or are we still in the clear?
The Climax: Unveiling the Existence of a Cycle
The suspense peaks as we look at the last remaining road, connecting intersections 3 and 4. These intersections are in separate neighborhoods, so once again, it's time for a merge.
Step 1: The Final Merge with Union(3, 4)
We're merging the neighborhoods of 3 and 4. Given that 3 is already the head of a large neighborhood {0, 1, 2, 3}, this merge will add 4 to this expanding community.
The Last Update on the Investigation Board
Step 2: Interpreting the Final State of the Parent Array
By updating the value under 3 to 4, we signify that 4 is now the head of this mega-neighborhood, representing the union set {0, 1, 2, 3, 4}. It's as if 4 has assumed the role of the ultimate community leader, consolidating all the smaller communities into one.
Step 3: The Moment of Truth
Now, let's pay attention to the last edge that connects 3 and 4. According to our parent array, both intersections are part of the same large neighborhood. Using our find operation, we discover:
1Find(3) = 4
2Find(4) = 4The results are clear as day. Both 3 and 4 are part of the same neighborhood, which means we've found a cycle!

The Final Verdict: A Cycle Detected!
That's our "Aha!" moment! Finding that both elements belong to the same group confirms the presence of a cycle in this graph. Our detective journey using the Union-Find algorithm has reached its pinnacle, successfully revealing a loop in our network of roads.
xxxxxxxxxx}// Initialize the parent array to represent isolated neighborhoods.int[] parent = {0, 1, 2, 3, 4};// Define the find function to identify the 'root' or 'parent' of each neighborhood.public int find(int vertex) { if (parent[vertex] == vertex) { return vertex; } return find(parent[vertex]);}// Define the Union function to merge neighborhoods.public void union(int vertex1, int vertex2) { int root1 = find(vertex1); int root2 = find(vertex2); parent[root1] = root2;}// Merging previous neighborhoods.union(0, 1); // Merging 0 and 1union(1, 2); // Merging 1 and 2union(2, 3); // Merging 2 and 3// Investigate the last remaining road connecting intersections 3 and 4.union(3, 4);// Display the updated parent array.System.out.println("Updated Parent Array: " + Arrays.toString(parent));The Time Complexity of Union-Find
The Basic Model: Union-Find Without Optimizations
In its most basic form, without any clever tricks up its sleeve, the Union-Find algorithm can be a bit sluggish.
Time Complexity for Basic Operations
- Find Operation:
- Union Operation:
This means that for every Find or Union operation, you could potentially have to traverse all vertices. Imagine having to knock on every door in the neighborhood to find one person—it's effective but not efficient!
Why This Matters
The time complexity tells us how the algorithm's performance scales with the size of the input. may be acceptable for small graphs, but as the number of vertices and edges grows, so does the time it takes to perform each operation.
Understanding the complexities helps you make informed decisions when applying the algorithm in different scenarios.
Applications of the Algorithm
Some of the popular use cases of the Union-Find algorithm include:
The Union-Find algorithm proves useful in numerous scenarios:
- Network Connectivity: It can detect if two nodes in a network are connected.
- Cyclicality in Graphs: It can ascertain the presence of cycles in an undirected graph. If, while adding an edge, both vertices belong to the same subset, a cycle exists.
1def isCycle(graph):
2 parent = [-1] * len(graph)
3
4 def find(x):
5 if parent[x] == -1:
6 return x
7 return find(parent[x])
8
9 def union(x, y):
10 xset = find(x)
11 yset = find(y)
12 if xset != yset:
13 parent[xset] = yset
14
15 for i in range(len(graph)):
16 for j in graph[i]:
17 x = find(i)
18 y = find(j)
19 if x == y:
20 return True
21 union(i, j)
22
23 return False- Kruskal’s Minimum Spanning Tree Algorithm: It's employed to detect the shortest possible tree that connects all nodes in a graph.
- Image Segmentation: In computer vision, it helps in segmenting an image into multiple regions or objects.
- Grid percolation
- Network Connectivity
- Least common ancestor in trees
Wrapping Up: The Essence of Union-Find
In this interactive exploration, we've journeyed through the realms of the Union-Find algorithm, diving deep into its implementation and use-cases. Imagine it as a masterful detective who's brilliant at solving the mysteries of connected neighborhoods, all while keeping a vigilant eye for cycles or loops.
The Core Philosophy: Uniting and Finding Efficiently
Union-Find shines in scenarios that require frequent merging of sets or neighborhoods. It's like a social organizer who's adept at bringing people together into bigger friend circles, all while being able to quickly identify who belongs to which circle. That's the soul of Union-Find—creating unions and finding memberships efficiently!
The Power of Optimization
While our detective is quite competent, they can be made even more efficient with some clever techniques:
- Path Compression: Think of this as placing signposts that direct you faster to the head of the neighborhood.
- Union by Rank: This is akin to merging smaller friend circles into larger ones, ensuring that the social structure remains balanced.
Your Turn: Time to Flex Those Skills
Now that you're well-acquainted with this brilliant detective of an algorithm, it's your turn to solve some intriguing mysteries:
Are you ready to apply Union-Find to solve these challenges?
One Pager Cheat Sheet
- In this lesson, we'll learn about how to use the
Union-Find algorithmto solve the problem of network connectivity by exploringgraphsand optimizing for efficiency. - The Union-Find algorithm is an algorithmic technique
that keeps track of a set of elements partitioned or split into a number of disjoint (non-overlapping) subsetsand uses theFindandUnionmethods to determine if two elements are in the same subset and model the actual connection/path between the two objects. - You can apply the Union-Find algorithm on disjoint
subsetstofindandunionelements, efficiently solving problems such as determining if agraphis cyclic or not. - A real-world example of the Union-Find algorithm involves creating
subsetsfor each edge in order to determine if two vertices of the same vertices belong to the samesubset, thereby confirming the presence of a cycle. - We will loop through the edges to check if the graph is cyclic or not, and if it is acyclic, our parent array representation will show the final subsets.
- Using the array indices as IDs, we are modeling parent-child relationships between the edges, and by changing the the value at index
0to1, we are saying0is the parent of1which is now representative of the union setUnion(0, 1). - We need to
unionthe sets and replace -1 with 2 to indicate the change, then take the edge connecting1and3. - Replace -1 in 2 with 3, merge the sets of 1, 2 and 3, 4, and take the edge connecting 1 and 4.
- The two elements 3 and 4 are in different sets so we need to
unionthem to create a single edge between them. - The Union-Find algorithm requires optimizations like
path compression,union by rankandunion by sizeto achieveO(n)time for theUnionandFindoperations. - The Union-Find algorithm, which can be optimized with techniques such as
path compressionandunion by rank, is commonly used to perform merge-operations.

